Простейшие тригонометрические уравнения.
1. sinx = a, |a|![]() 1
1
x = (–1 ) k arcsin a + ![]() k , k
k , k ![]()
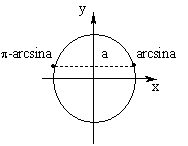
Частные случаи:
| a = –1 | a = 0 | a = 1 |
| sinx = –1 | sin x = 0 | sin x = |
| x = – | x = | x = |
| | | |
| | | a| 1 корней нет | |
2. cos x = a , |a|![]() 1
1
x = ± arccos a + 2![]() k , k
k , k ![]()
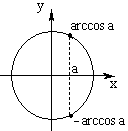
Частные случаи:
| a = –1 | a = 0 | a = 1 |
| cos x = –1 | cos x = 0 | cos x = 1 |
| x = | x = | x = 2 |
|
|
| |
| | |a| 1 корней нет | |
3. tg x = a , a
x = ± arctg a + ![]() k , k
k , k ![]()
Основные типы тригонометрических уравнений.
Уравнения, сводящиеся к простейшим.
Уравнения, сводящиеся к квадратным.
Однородные уравнения: asinx + bcosx = 0, a sin 2 x + b sinxcosx + c cos 2 x = 0.
Уравнения вида a sinx + b cosx = с , с ≠ 0.
Уравнения, решаемые разложением на множители.
Нестандартные уравнения.
Тригонометрическое уравнение — уравнение, содержащее неизвестное под знаком тригонометрической функции.
Основные методы решения тригонометрических уравнений.
1. Метод разложения на множители
Если уравнение f(x)=0 удаётся преобразовать к виду f1(x)⋅f2(x)=0, то либо f1(x)=0, либо f2(x)=0.
В подобных случаях задача сводится к решению совокупности уравнений: f1(x)=0; f2(x)=0.
Пример:
решить уравнение методом разложения на множители (sinx−13)(cosx+25)=0.
Задача сводится к решению совокупности уравнений: sinx=13;cosx=−25.
Из этих уравнений находим соответственно: x=(−1)karcsin13+πk,k∈Z;x=±arccos(−25)+2πk,k∈Z.
Обрати внимание!
Учти, что переход от уравнения f1(x)⋅f2(x)=0 к совокупности уравнений f1(x)=0; f2(x)=0 не всегда безопасен.
Пример:
рассмотрим уравнение tgx(sinx−1)=0.
Из уравнения tgx=0 находим: x=πk,k∈Z.
Из уравнения sinx=1 находим: x=π2+2πk,k∈Z.
Но включить оба решения в ответ нельзя, т. к. при значениях x=π2+2πk,k∈Z, входящий в заданное уравнение множитель tgx не имеет смысла, т. е. значения x=π2+2πk,k∈Z, не принадлежат области определения уравнения, это посторонние корни.
2. Метод введения новой переменной
Пример:
решить уравнение методом введения новой переменной 2sin2x−5sinx+2=0.
Введём новую переменную z=sinx, тогда уравнение можно записать как 2z2−5z+2=0.
Находим корни данного уравнения: z1=2,z2=12. Значит, либо sinx=2, либо sinx=12.
Уравнение sinx=2 не имеет корней, а из уравнения sinx=12 находим: x=(−1)karcsin12+πk,k∈Z;x=(−1)kπ6+πk,k∈Z.

 Получите свидетельство
Получите свидетельство Вход
Вход













 Исследовательская работа по теме Тригонометрические уравнения и методы рационализации их решения (32.21 KB)
Исследовательская работа по теме Тригонометрические уравнения и методы рационализации их решения (32.21 KB)
 0
0 213
213 5
5 Нравится
0
Нравится
0


