ВВЕДЕНИЕ
От того, как заложены элементарные математические представления в значительной мере зависит весь дальнейший путь математического развития человека. Основным понятием элементарной математики является понятие числа.
Между тем учащиеся нередко допускают ошибки, смешивая понятия «число» и «цифра». Так мы часто слышим, такие высказывания: «Надоело считать эти цифры», «Загадай любую цифру от 1 до 100», «Расскажите о больших цифрах».
Понятия «цифра» и «число» путают даже взрослые. Очень часто, посмотрев хороший фильм или прочитав книгу, мы подхватываем несколько выражений оттуда. И эти цитаты из фильмов и книг вживаются в нашу речь и следуют вместе с нами. Но писатели и авторы фильмов тоже могут путать понятия «цифра» и «число».
Актуальность нашей исследовательской работы заключается в том, что для успешного изучения школьной математики у учащихся должны быть четко сформированы понятия «число» и «цифра».
Проблема: у учащихся понятие «число» и «цифра» не всегда сформированы на высоком уровне. А огромный поток недостоверной информации из печатных изданий, по телевидению, интернет только усугубляет данную проблему. Понятие числа служит исходным для многих математических теорий. Числа находят широкое применение в физике, механике, астрономии, химии, информатике и многих других науках. Поэтому учащиеся, не владеющие понятиями «число» и «цифра» могут испытывать затруднения в обучении.
Цель исследования: изучение уровня владения учащимися школы понятиями «число» и «цифра».
Для достижения поставленной цели необходимо решить следующие задачи:
Изучить историю возникновения понятий «число» и «цифра»
Выявить сущности используемых понятий «число» и «цифра»
Разработать анкету для получения информации о степени владения понятиями «число» и «цифра». Выяснить уровень владения понятиями «число» и «цифра» через анкетирование
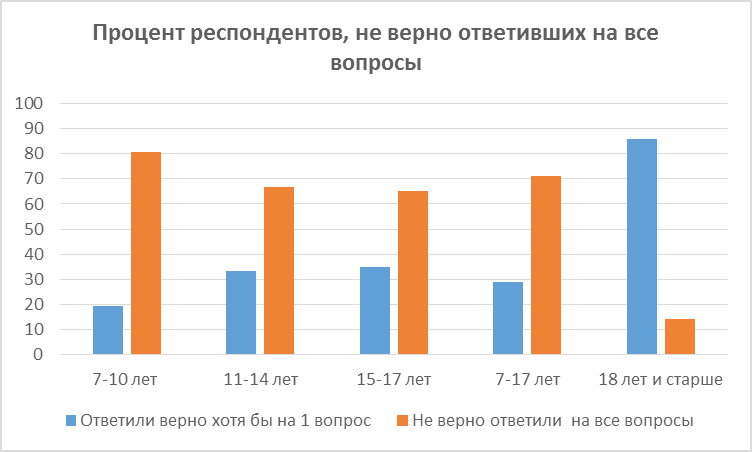
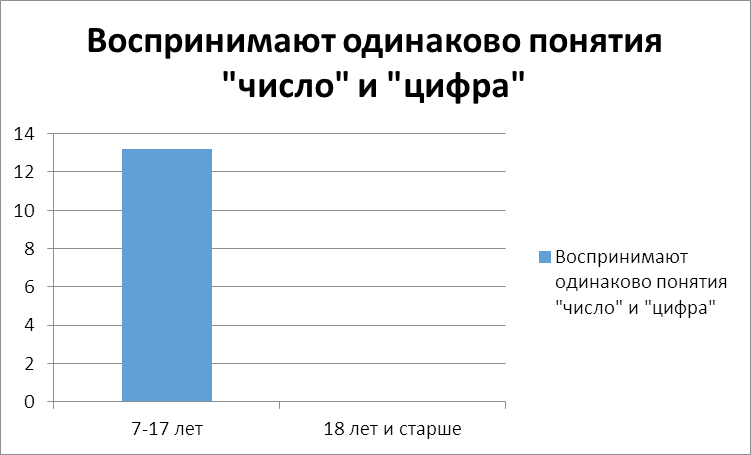
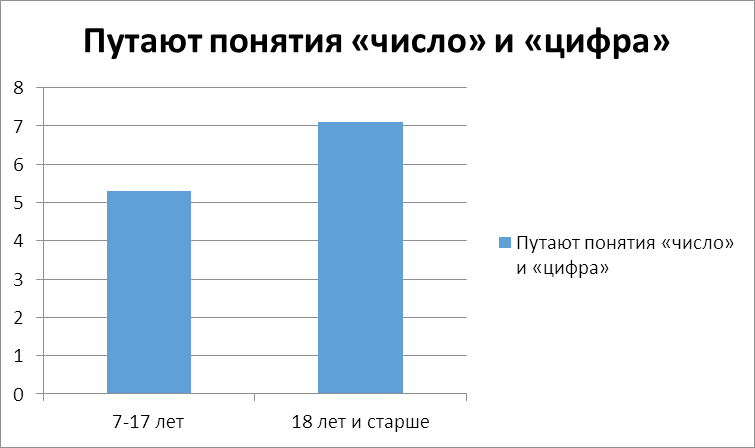
Сравнить результаты анкетирования среди разных возрастных групп. Сделать выводы об уровне владения учащимися понятиями «число» и «цифра»
Познакомить учащихся, учителей, родителей с результатами исследования
Объект исследования: на примере учащихся Пойловской средней общеобразовательной школы.
Предмет исследования: уровень владения понятиями «число» и «цифра» учащимися школы.
Гипотеза: мы предполагаем, что учащиеся школы не владеют понятиями «число» и «цифра».
В ходе исследования применялись следующие методы:
Анализ и синтез информации
Наблюдение
Сравнение
Метод анкетирования
Математическое моделирование, графическая интерпретация.
Новизна: изучение уровня владения учащимися понятиями «число» и «цифра» в нашей школе ранее никто не проводил.
Для исследования темы был проведен теоретический анализ научной литературы: Белова Л. С. «Большая энциклопедия знаний»; Волков М. В. «Собеседник школьника»; Депман И. Я. «Мир чисел»; Дмитриева Н. Ю. «Универсальный справочник школьника», где мы получили общую необходимую информацию, познакомились с историей возникновения понятий «число» и «цифра». Из книги Макарова Н. В. Информатика и ИКТ; мы узнали о различных системах счисления. Новый толково-словообразовательный словарь русского языка под ред. Т. Ф. Ефремовой; толковый словарь русского языка Ожегов С. И. и Шведова Н. Ю. ; свободная энциклопедия Википедия помогли нам разобраться в сущности используемых понятий «число» и «цифра».
Наша работа может использоваться учителями математики на уроках и для внеклассных мероприятий, родителями для правильного формирования у своих детей понятий «число» и «цифра», учащимися для самообразования. С помощью нашей работы можно узнать историю происхождения понятий «число» и «цифра», легко разобраться в сущности понятий «число» и «цифра», понять, чем число отличается от цифры.

ОСНОВНАЯ ЧАСТЬ. КАК УЧАЩИЕСЯ ШКОЛЫ ВЛАДЕЮТ ПОНЯТИЯМИ «ЧИСЛО» И «ЦИФРА»?
ИСТОРИЯ ВОЗНИКНОВЕНИЯ ПОНЯТИЙ «ЧИСЛО» И «ЦИФРА»
Когда речь идёт о чём – то очень простом, понятном, мы часто говорим: «Дело ясно, как дважды два – четыре!»
А ведь прежде чем додуматься до того, что дважды два – четыре, людям пришлось учиться много, много тысяч лет. Конечно, это учение шло не за партой. Человек постепенно учился жить: строить жилище, находить дорогу в дальних походах, обрабатывать землю. И одновременно он учился считать. Потому что даже в самые далёкие времена, когда люди жили в пещерах, они не могли обойтись без счёта и меры, тогда человек не знал таких слов, как «Пять» или «Семь», но он мог показывать числа на пальцах рук. В разговорной речи мы до сих пор иногда слышим: «Дай пять!», то есть подай руку. А раньше говорили: «Дай пясть!» Пясть — это рука, а на руке пять пальцев. Когда-то слово пять имело конкретное значение — пять пальцев пясти, то есть руки. Или такое выражение: «Знаю, как свои пять пальцев». Не с того ли далёкого времени пошли эти выражения, когда знать, что пальцев пять, значило то же, что уметь считать?[3]
Понятие о числе зародилось в глубокой древности, когда человек научился считать предметы: два дерева, семь быков, пять рыб. Сначала счёт вели на пальцах. Но проходили многие – многие годы. Менялась жизнь человека. Люди приручили животных, и на земле появились первые скотоводы, а затем и земледельцы. Постепенно росли знания людей, и чем дальше, тем больше увеличивалась потребность в умении считать. Скотоводам приходилась пересчитывать свои стада, а при этом счёт мог идти уже сотнями и тысячами. Земледельцу надо было знать, сколько земли засеять, чтобы прокормить себя до следующего урожая.
Позднее вместо пальцев для счёта начали использовать зарубки на палочках. А когда возникла письменность, для обозначения чисел стали употреблять буквы. Например, у славян буква А означала число «один» (Б не имело числового значения) , В — два, Г — три, Д — четыре, Е — пять.
Постепенно люди стали осознавать числа независимо от предметов и лиц, которые могли подвергаться счёту: просто число «два» или число «семь». В связи с этим у славян появилось слово число. В значении «счёт, величина, количество» его начали употреблять в русском языке с ХI века. Наши предки использовали слово число и для указания на дату, год. С ХIII века оно стало обозначать ещё и дань, подать. В старину в книжном русском языке наряду со словом число имело хождение существительное чисмя, а также прилагательное чисменый. В ХVI веке появился глагол числити — «считать». [16]
Во второй половине ХV века в европейских странах получили широкое распространение специальные знаки, обозначающие числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Это изобретение было сделанным в Индии. Индийцы изобрели современные цифры, изобрели ноль, позволивший экономно и точно записывать любые числа. От индийцев эти цифры распространились через Иран к арабам, и затем уже арабы занесли их в Европу. Мы называем их арабскими цифрами, тогда как в действительности эти цифры индийские.
Арабские цифры происходят от индийских символов для записи чисел. Арабские цифры были видоизменёнными изображениями индийских цифр, приспособленными к арабскому письму.
Впервые индийскую систему записи использовал арабский учёный Мухаммед ибн Муса аль-Хорезми, автор знаменитой Китаб аль-Джебр ва-ль-Мукабаля, от названия которой произошёл термин «алгебра». Арабский учёный Мухаммед ибн Мусса аль - Хорезми упростил индийскую систему нумерации и разработал обоснованную систему начертания цифр. Многие из цифр уже тогда были похожи на цифры, которые мы сейчас применяем. [17]
Арабские цифры стали известны европейцам благодаря их изображениям на косточках абака. Для экономии места они изображались боком. Поэтому, в частности, цифры «2» и «3» приобрели ту форму, которую мы знаем. Европейская цифра «8» никак не связана с арабским эквивалентом. Её изображение происходит из сокращённой записи латинского слова octo («восемь») . [1]
Название «арабские цифры» — дань исторической роли арабской культуры в популяризации десятичной позиционной системы. В нашей стране арабские цифры появились в Петровскую эпоху (в начале ХVIII века) . В то же время в русский язык вошло слово цифра. Арабское по происхождению, оно тоже пришло к нам из европейских языков. У арабов первоначальное значение слова цифра — это нуль, пустое место. Именно в этом значении существительное цифра вошло во многие европейские языки, в том числе в русский. С середины ХVIII века слово цифра приобрело новое значение — знак числа.
Вывод: понятия «число» и «цифра» различаются и по значению, и по происхождению. Понятие о числе зародилось в глубокой древности. В русском языке его начали употреблять в значении «счёт, величина, количество» с ХI века. В начале ХVIII века в нашей стране появились арабские цифры. С середины ХVIII века слово цифра приобрело новое значение — знак числа.
2. СУЩНОСТЬ ПОНЯТИЙ «ЧИСЛО» И «ЦИФРА»
Существует несколько определений числа и цифры. Так, например, в свободной энциклопедии Википедия: «Число́ — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, и символы математических операций». [9]
В современном толковом словаре русского языка под ред. Т. Ф. Ефремовой: «Число - понятие, при помощи которого выражается количество и ведется счет. Цифра - знак для обозначения числа». [7]
В толковом словаре русского языка С. И. Ожегова и Н. Ю. Шведова: «Число - основное понятие математики величина, при помощи которой производится счёт. Цифра - знак, обозначающий число. Арабские цифры (1, 2, 3 и т. д. ) . Римские цифры (I, II, III и т. д. ) ». [8]
Число́ — это абстрактная сущность, используемая для описания количества. Числа записываются одной или несколькими цифрами. Цифра — это знак для обозначения числа. По аналогии с алфавитом — это буква. Буква обозначает звук. Цифра — число. В нашей культуре мы используем 33 буквы русского алфавита для записи слов, и 10 арабских цифр для записи чисел (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) . Для записи числа 34, мы используем цифры «3» и «4». Сами по себе цифры еще не определяют число. Например, с помощью тех же самых цифр мы можем записать и число 43, и число 4433 и т. п. Правила записи чисел с помощью цифр определяются принятой нотацией и системой счисления. Система счисления - это способ записи чисел с помощью заданного набора специальных знаков (цифр) . [9] Нотация - система условных обозначений. [9] То, чем мы пользуемся в обычной жизни называется десятичной нотацией. И достоинством любой нотации является возможность записывать любые числа, пользуясь лишь ограниченным набором цифр. Точно так же, как мы записываем все многообразие слов, используя лишь 33 буквы алфавита. [15]
Существуют системы позиционные и непозиционные. В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти. [5]
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число - два, три, четыре, шестнадцать и т. д. . . Следовательно, возможно бесконечное множество позиционных систем. Примеры позиционной системы счисления: двоичная (0, 1) , десятичная (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) , восьмеричная (0, 1, 2, 3, 4, 5, 6, 7) , шестнадцатеричная (0 1 2 3 4 5 6 7 8 9 A B C D E F) системы счисления. [5]
Цифры и числа различных систем счисления настолько не совпадают, что число одной системы может оказаться цифрой другой
В наши дни слова число и цифра употребляются и в других значениях. Например, когда мы спрашиваем: «Какое сегодня число?», то имеем в виду день месяца. Сочетания «в том числе», «из числа кого-нибудь», «в числе кого-то» обозначают состав, совокупность людей или предметов. А если мы доказываем что-то с цифрами в руках, то обязательно используем числовые показатели. Словом «цифра» называют также денежную сумму (цифра дохода, цифра гонорара) .
Число –одно из основных понятий математики, позволяющее выразить результаты счета или измерения.
Вывод: число́ — это абстрактная сущность, используемая для описания количества. Числа записываются одной или несколькими цифрами. Цифра — это знак для обозначения числа. Число –одно из основных понятий математики, позволяющее выразить результаты счета или измерения.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Исследовательская работа по математике "Как учащиеся школы владеют понятиями «число» и «цифра»?" (0.11 MB)
Исследовательская работа по математике "Как учащиеся школы владеют понятиями «число» и «цифра»?" (0.11 MB)
 1
1 2057
2057 256
256 Нравится
0
Нравится
0




