Получите свидетельство
Вход
Урок алгебры в 9 классе
- Решение линейных неравенств с одной переменной.
- Вспомним теоретические положения!
5 Х ≥ 5 х 5 (5;+ ∞) 5 х [ 5;+ ∞) " width="640"
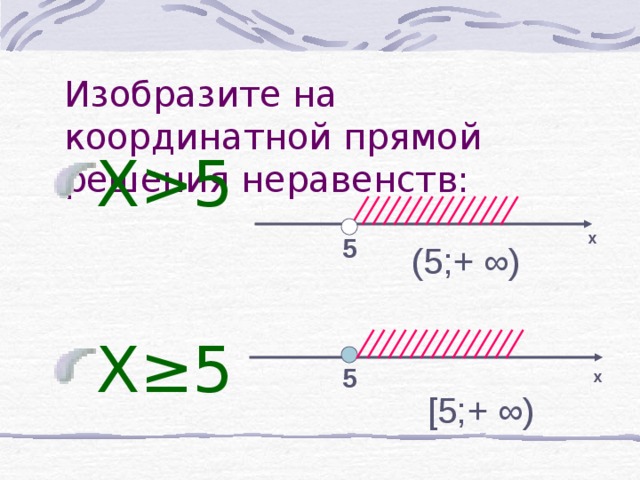
Изобразите на координатной прямой решения неравенств:
- Х 5
- Х ≥ 5
х
5
(5;+ ∞)
5
х
[ 5;+ ∞)
![-4 х≤3 3 -4 х х (-4;3 ]](https://fsd.videouroki.net/html/2017/11/07/v_5a020f2ab5c1a/img3.jpg)
-4 х≤3
3
-4
х
х
(-4;3 ]
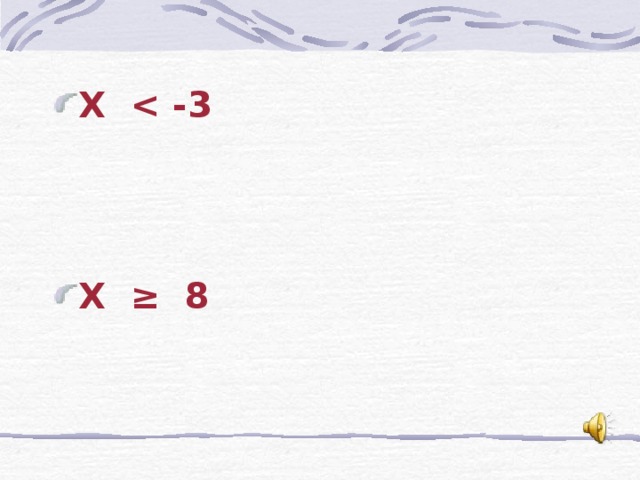
- Х
- Х ≥ 8
Карта
15 2) -4х -12 3) -1,8х 36 12у 120 2) -6х 1,8 3) -х -1 Проблемы? " width="640"
« Обдумай цель раньше, чем дело начать »
- 3х 15
2) -4х -12
3) -1,8х 36
- 12у 120
2) -6х 1,8
3) -х -1
Проблемы?
4 х х 2 ) –1/3 х х -6: (-1/3) х 6*3 х 18 х (18; + ) х (- ; -0,8) " width="640"
Инструкция
1 ) –0,5х 4
х
х
2 ) –1/3 х
х -6: (-1/3)
х 6*3
х 18
х (18; + )
х (- ; -0,8)
Вам помочь
«Усердие – мать удачи»
- 64-6у 1-у
- 30+5х 18-7х
-1 -12х -1-2 -12х -3 х х х 2) 16х-34 х+1 16х-х 1+34 15х 35 х 35:15 х 35/15 х 7/3 х (- ; ¼) х [ 7/3; + ) " width="640"
Инструкция
1) 2-12х -1
-12х -1-2
-12х -3
х
х
х
2) 16х-34 х+1
16х-х 1+34
15х 35
х 35:15
х 35/15
х 7/3
х (- ; ¼)
х [ 7/3; + )
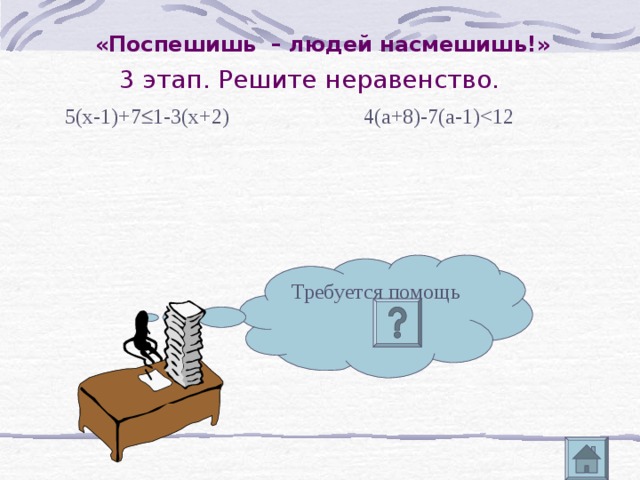
«Поспешишь – людей насмешишь!»
3 этап. Решите неравенство.
4(а+8)-7(а-1)
5(х-1)+7 1-3(х+2)
Требуется помощь
![2(3-в)-3(2+в) в 6-2в-6-3в в 5в в -5в-в 0 -6в 0 в 0: (-6) в 0 4(2-3х)-(5-х) 11-х 8-12х-5+х 11-х -12х+х+х 11-8+5 -10х 8 х 8: (-10) х -0,8 х (- ; -0,8 ] в [ 0; + )](https://fsd.videouroki.net/html/2017/11/07/v_5a020f2ab5c1a/img11.jpg)
2(3-в)-3(2+в) в
6-2в-6-3в в
5в в
-5в-в 0
-6в 0
в 0: (-6)
в 0
4(2-3х)-(5-х) 11-х
8-12х-5+х 11-х
-12х+х+х 11-8+5
-10х 8
х 8: (-10)
х -0,8
х (- ; -0,8 ]
в [ 0; + )
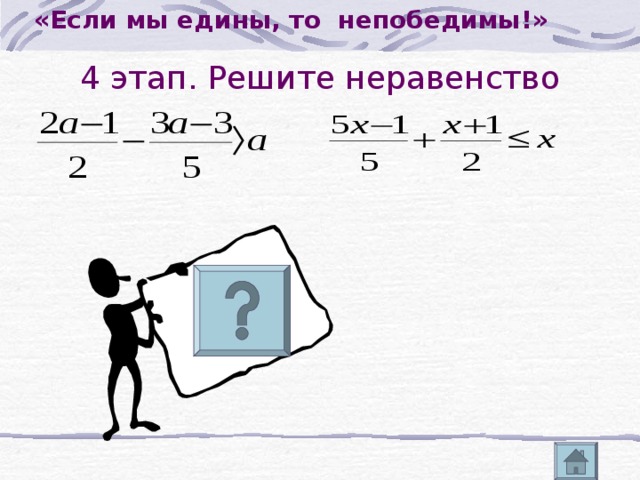
«Если мы едины, то непобедимы!»
4 этап. Решите неравенство
17 х (17; + ) " width="640"
Инструкция
3(3+х)+4(2-х) 0
9+3х+8-4х 0
17-х 0
-х -17
х 17
х (17; + )
«Один за всех,
все – за одного!»
b , с 0 a = b + c Докажем : a = b Доказательство : a b , значит а- b0 . Пусть a = b + c (a – b) a = (b + c) (a – b) a2 – ab = ab – b2 + ac – bc a2 – ab – ac = ab – b2 – bc a (a – b – c) = b (a – b – c) a = b , ч.т.д. " width="640"
Софизм – док-во ложного утверждения, причем ошибка в док-ве искусно замаскирована. Софистами- называли группу древнегреческих ученых-философов IV –V в.в. до н.э., достигших большого искусства в логике. Дано : a b , с 0 a = b + c Докажем : a = b Доказательство : a b , значит а- b0 . Пусть a = b + c (a – b) a = (b + c) (a – b) a2 – ab = ab – b2 + ac – bc a2 – ab – ac = ab – b2 – bc a (a – b – c) = b (a – b – c) a = b , ч.т.д.
- Что нового вы узнали на уроке?
- Что понравилось на уроке?
- Что не понравилось?
- Все ли было понятно?
- Довольны ли вы своей работой на уроке?
Интерактивный урок алгебры в 9 классе на тему: "Решение линейных неравенств с одной переменной" (556 KB)
0
2074
440
Нравится
1
