
Автор работы:
учитель информатики и ИКТ МОУ «Тверской лицей» Соболева Ирина Леонидовна
Тверь, 2012
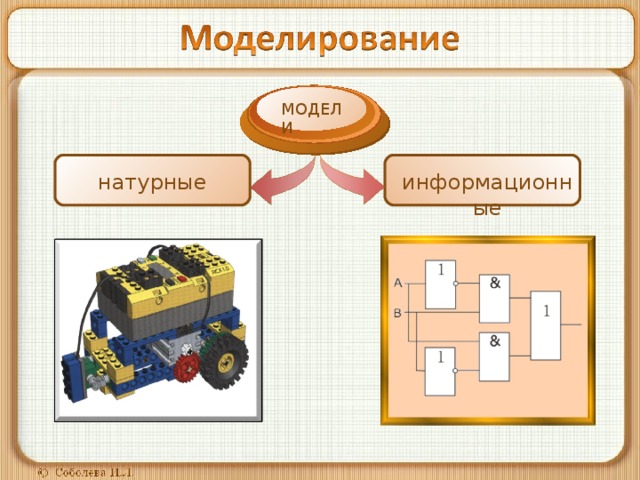
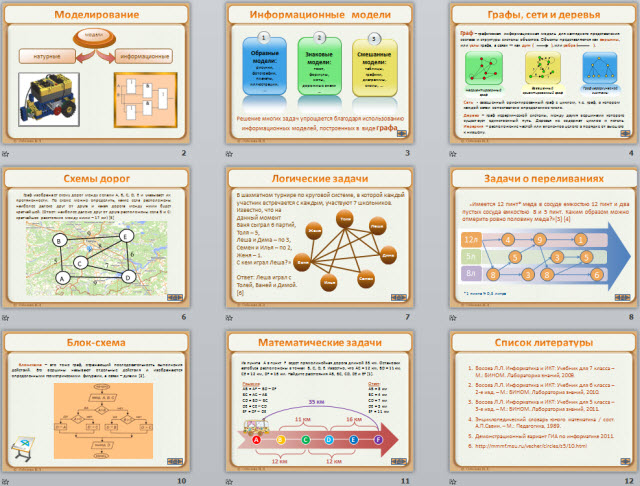
МОДЕЛИ
натурные
информационные
2
1
3
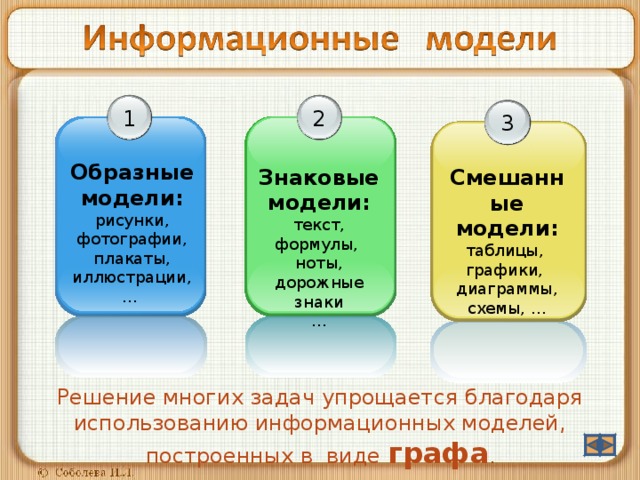
Образные модели:
рисунки, фотографии,
плакаты,
иллюстрации,
…
Знаковые модели:
текст,
формулы,
ноты,
дорожные знаки
…
Смешанные модели:
таблицы,
графики,
диаграммы,
схемы, …
Решение многих задач упрощается благодаря использованию информационных моделей, построенных в виде графа .
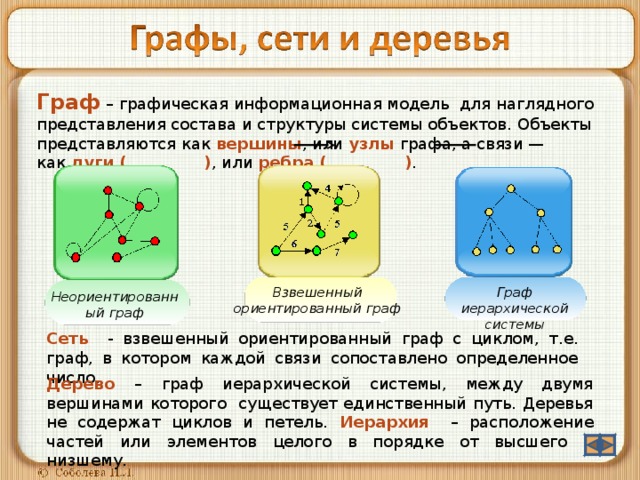
Граф – графическая информационная модель для наглядного представления состава и структуры системы объектов. Объекты представляются как вершины , или узлы графа, а связи — как дуги ( ) , или ребра ( ) .
Граф иерархической системы
Взвешенный ориентированный граф
Неориентированный граф
Сеть - взвешенный ориентированный граф с циклом, т.е. граф, в котором каждой связи сопоставлено определенное число.
Дерево – граф иерархической системы, между двумя вершинами которого существует единственный путь. Деревья не содержат циклов и петель. Иерархия – расположение частей или элементов целого в порядке от высшего к низшему.
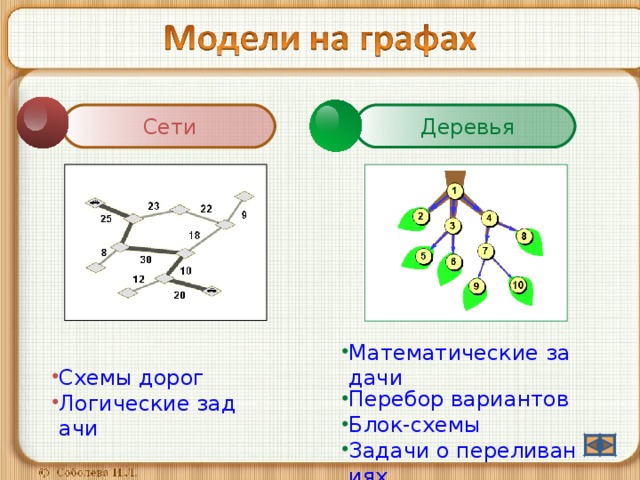
Деревья
Сети
- Математические задачи
- Перебор вариантов
- Блок-схемы
- Задачи о переливаниях
- Схемы дорог
- Логические задачи
![9 6 8 7 9 5 B A C D E Граф изображает схему дорог между селами A , B, C , D , E и указывает их протяженности. По схеме можно определить, какие села расположены наиболее далеко друг от друга и какая дорога между ними будет кратчайшей. (Ответ: наиболее далеко друг от друга расположены села B и C : кратчайшее расстояние между ними – 17 км) [5]](https://fsd.videouroki.net/html/2012/05/04/98658875/img5.jpg)
9
6
8
7
9
5
B
A
C
D
E
Граф изображает схему дорог между селами A , B, C , D , E и указывает их протяженности. По схеме можно определить, какие села расположены наиболее далеко друг от друга и какая дорога между ними будет кратчайшей. (Ответ: наиболее далеко друг от друга расположены села B и C : кратчайшее расстояние между ними – 17 км) [5]
![В шахматном турнире по круговой системе, в которой каждый участник встречается с каждым, участвуют 7 школьников. Известно, что на данный момент Ваня сыграл 6 партий, Толя – 5, Леша и Дима – по 3, Семен и Илья – по 2, Женя – 1. С кем играл Леша?» Ответ: Леша играл с Толей, Ваней и Димой. [6] Толя Леша Женя Дима Ваня Семен Илья](https://fsd.videouroki.net/html/2012/05/04/98658875/img6.jpg)
В шахматном турнире по круговой системе, в которой каждый участник встречается с каждым, участвуют 7 школьников.
Известно, что на данный момент Ваня сыграл 6 партий, Толя – 5, Леша и Дима – по 3, Семен и Илья – по 2, Женя – 1. С кем играл Леша?»
Ответ: Леша играл с Толей, Ваней и Димой. [6]
Толя
Леша
Женя
Дима
Ваня
Семен
Илья
![« Имеется 12 пинт * меда в сосуде емкостью 12 пинт и два пустых сосуда емкостью 8 и 5 пинт. Каким образом можно отмерить ровно половину меда?»[3] [4] 1 9 4 5 5 3 6 8 3 8 * 1 пинта ≈ 0,5 литра](https://fsd.videouroki.net/html/2012/05/04/98658875/img7.jpg)
« Имеется 12 пинт * меда в сосуде емкостью 12 пинт и два пустых сосуда емкостью 8 и 5 пинт. Каким образом можно отмерить ровно половину меда?»[3] [4]
1
9
4
5
5
3
6
8
3
8
* 1 пинта ≈ 0,5 литра
![«Стой, братцы, стой!» кричит Мартышка: «погодите! Как музыке идти? Ведь вы не так сидите. Ты с басом, Мишенька, садись против альта, Я, прима, сяду против вторы; Тогда пойдет уж музыка не та: У нас запляшут лес и горы!» Расселись, начали Квартет; Он всё-таки на лад нейдет. И.А.Крылов «Квартет» Сколько всего могло быть вариантов расположения незадачливых музыкантов, если Мишка всегда сидел на своем месте? Ответ : возможно 6 вариантов расположения музыкантов во главе с Мишкой [1] .](https://fsd.videouroki.net/html/2012/05/04/98658875/img8.jpg)
«Стой, братцы, стой!» кричит Мартышка: «погодите! Как музыке идти? Ведь вы не так сидите. Ты с басом, Мишенька, садись против альта, Я, прима, сяду против вторы; Тогда пойдет уж музыка не та: У нас запляшут лес и горы!» Расселись, начали Квартет; Он всё-таки на лад нейдет.
И.А.Крылов «Квартет»
Сколько всего могло быть вариантов расположения незадачливых музыкантов, если Мишка всегда сидел на своем месте?
Ответ : возможно 6 вариантов расположения
музыкантов во главе с Мишкой [1] .
![Блок-схема – это тоже граф, отражающий последовательность выполнения действий. Его вершины называют отдельные действия и изображаются определенными геометрическими фигурами, а связи – дугами [2].](https://fsd.videouroki.net/html/2012/05/04/98658875/img9.jpg)
Блок-схема – это тоже граф, отражающий последовательность выполнения действий. Его вершины называют отдельные действия и изображаются определенными геометрическими фигурами, а связи – дугами [2].
![Из пункта A в пункт F ведет прямолинейная дорога длиной 35 км. Остановки автобуса расположены в точках B, C, D, E . Известно, что AC = 12 км, BD = 11 км, CE = 12 км, DF = 16 км. Найдите расстояния AB, BC, CD, DE и EF [1] . Ответ : Решение : AB = 8 км BC = 4 км CD = 7 км DE = 5 км EF = 11 км AB = AF – BD – DF BC = AC – AB CD = BD – BC DE = CE – CD EF = DF – DE 35 км 16 км 1 1 км F E D C B A 12 км 12 км](https://fsd.videouroki.net/html/2012/05/04/98658875/img10.jpg)
Из пункта A в пункт F ведет прямолинейная дорога длиной 35 км. Остановки автобуса расположены в точках B, C, D, E . Известно, что AC = 12 км, BD = 11 км, CE = 12 км, DF = 16 км. Найдите расстояния AB, BC, CD, DE и EF [1] .
Ответ :
Решение :
AB = 8 км
BC = 4 км
CD = 7 км
DE = 5 км
EF = 11 км
AB = AF – BD – DF
BC = AC – AB
CD = BD – BC
DE = CE – CD
EF = DF – DE
35 км
16 км
1 1 км
F
E
D
C
B
A
12 км
12 км

- Босова Л.Л. Информатика и ИКТ: Учебник для 7 класса – М.: БИНОМ. Лаборатория знаний, 2009.
- Босова Л.Л. Информатика и ИКТ: Учебник для 6 класса – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2010.
- Босова Л.Л. Информатика и ИКТ: Учебник для 5 класса – 3-е изд. – М.: БИНОМ. Лаборатория знаний, 2011.
- Энциклопедический словарь юного математика / c ост. А.П.Савин. – М.: Педагогика, 1989.
- Демонстрационный вариант ГИА по информатике 2011.
- http://mmmf.msu.ru/vecher/circles/z5/10.html


 Получите свидетельство
Получите свидетельство Вход
Вход








![9 6 8 7 9 5 B A C D E Граф изображает схему дорог между селами A , B, C , D , E и указывает их протяженности. По схеме можно определить, какие села расположены наиболее далеко друг от друга и какая дорога между ними будет кратчайшей. (Ответ: наиболее далеко друг от друга расположены села B и C : кратчайшее расстояние между ними – 17 км) [5]](https://fsd.videouroki.net/html/2012/05/04/98658875/img5.jpg)
![В шахматном турнире по круговой системе, в которой каждый участник встречается с каждым, участвуют 7 школьников. Известно, что на данный момент Ваня сыграл 6 партий, Толя – 5, Леша и Дима – по 3, Семен и Илья – по 2, Женя – 1. С кем играл Леша?» Ответ: Леша играл с Толей, Ваней и Димой. [6] Толя Леша Женя Дима Ваня Семен Илья](https://fsd.videouroki.net/html/2012/05/04/98658875/img6.jpg)
![« Имеется 12 пинт * меда в сосуде емкостью 12 пинт и два пустых сосуда емкостью 8 и 5 пинт. Каким образом можно отмерить ровно половину меда?»[3] [4] 1 9 4 5 5 3 6 8 3 8 * 1 пинта ≈ 0,5 литра](https://fsd.videouroki.net/html/2012/05/04/98658875/img7.jpg)
![«Стой, братцы, стой!» кричит Мартышка: «погодите! Как музыке идти? Ведь вы не так сидите. Ты с басом, Мишенька, садись против альта, Я, прима, сяду против вторы; Тогда пойдет уж музыка не та: У нас запляшут лес и горы!» Расселись, начали Квартет; Он всё-таки на лад нейдет. И.А.Крылов «Квартет» Сколько всего могло быть вариантов расположения незадачливых музыкантов, если Мишка всегда сидел на своем месте? Ответ : возможно 6 вариантов расположения музыкантов во главе с Мишкой [1] .](https://fsd.videouroki.net/html/2012/05/04/98658875/img8.jpg)
![Блок-схема – это тоже граф, отражающий последовательность выполнения действий. Его вершины называют отдельные действия и изображаются определенными геометрическими фигурами, а связи – дугами [2].](https://fsd.videouroki.net/html/2012/05/04/98658875/img9.jpg)
![Из пункта A в пункт F ведет прямолинейная дорога длиной 35 км. Остановки автобуса расположены в точках B, C, D, E . Известно, что AC = 12 км, BD = 11 км, CE = 12 км, DF = 16 км. Найдите расстояния AB, BC, CD, DE и EF [1] . Ответ : Решение : AB = 8 км BC = 4 км CD = 7 км DE = 5 км EF = 11 км AB = AF – BD – DF BC = AC – AB CD = BD – BC DE = CE – CD EF = DF – DE 35 км 16 км 1 1 км F E D C B A 12 км 12 км](https://fsd.videouroki.net/html/2012/05/04/98658875/img10.jpg)











 Информационные модели на графах (3.01 MB)
Информационные модели на графах (3.01 MB)
 0
0 855
855 40
40 Нравится
0
Нравится
0






