Графы решения задач

ИСТОРИЯ ВОЗНИКНОВЕНИЯ ТЕОРИИ ГРАФОВ

1736 год,  г.Кёнигсберг. Через город протекает река Прегеля. В городе - семь мостов, расположенных так, как показано на рисунке. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках - проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог. 

Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. Причем, он решил не только эту конкретную задачу, но придумал общий метод решения подобных задач. При решении задачи о Кенигсбергских мостах Эйлер поступил следующим образом: он "сжал" сушу в точки, а мосты "вытянул" в линии. Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют  ГРАФОМ . 

Граф

Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.

Примерами графов

в нашей жизни

служат компьютерные

сети, пути сообщения

транспорта и т.п.

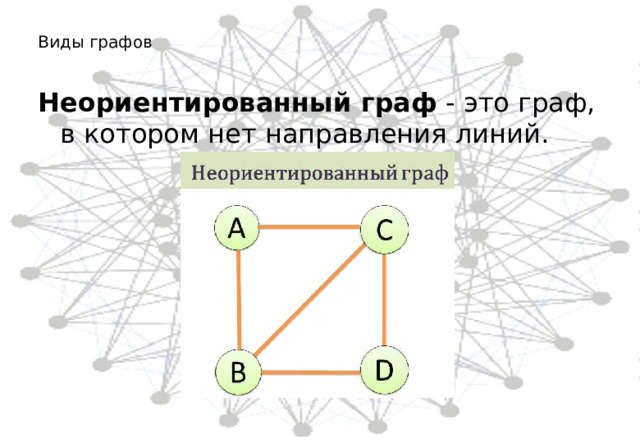
Виды графов

Неориентированный граф  - это граф, в котором нет направления линий.

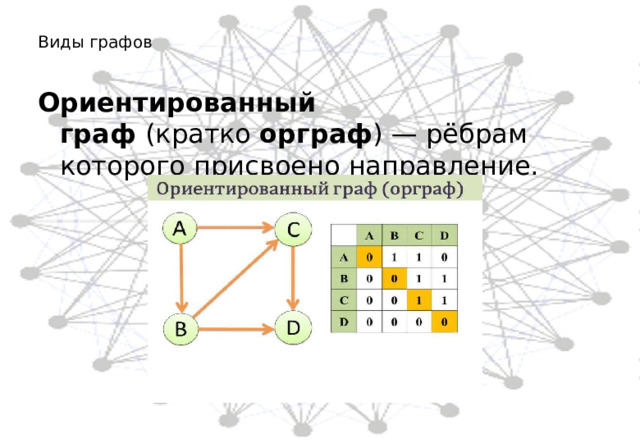
Виды графов

Ориентированный граф  (кратко  орграф ) — рёбрам которого присвоено направление. 

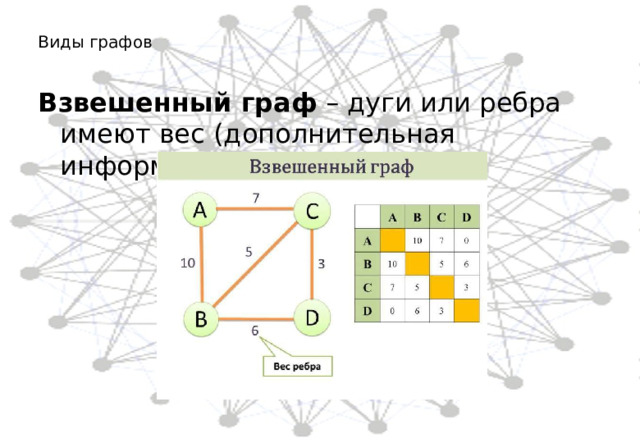
Виды графов

Взвешенный граф  – дуги или ребра имеют вес (дополнительная информация). 

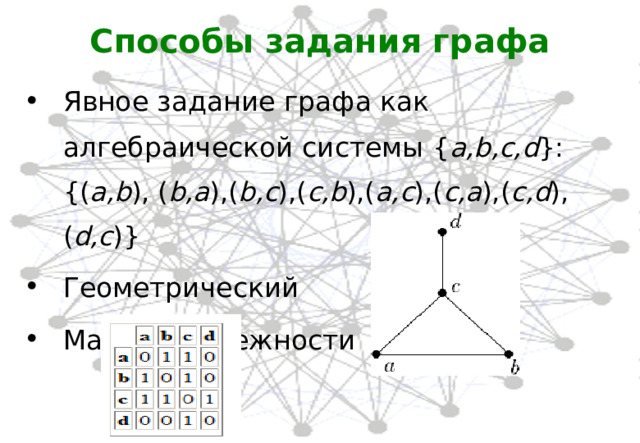
Способы задания графа

• Явное задание графа как алгебраической системы { a,b,c,d } : {( a,b ), ( b,a ),( b,c ),( c,b ),( a,c ),( c,a ),( c,d ),( d,c )}
• Геометрический
• Матрица смежности

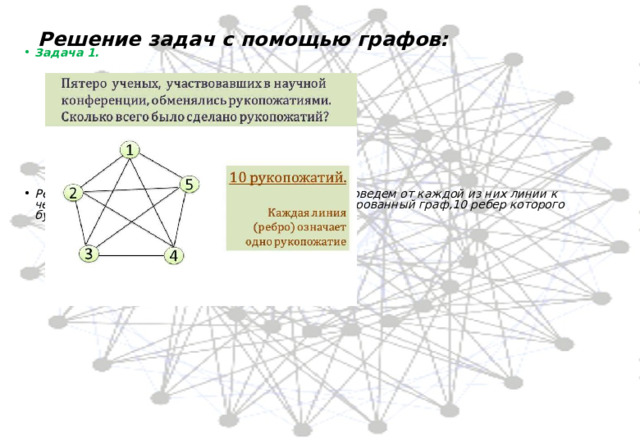
Решение задач с помощью графов:

• Задача 1.  

• Решение: Обозначим ученых вершинами графа и проведем от каждой из них линии к четырем другим . В результате получаем неориентированный граф,10 ребер которого будут считаться рукопожатиями.

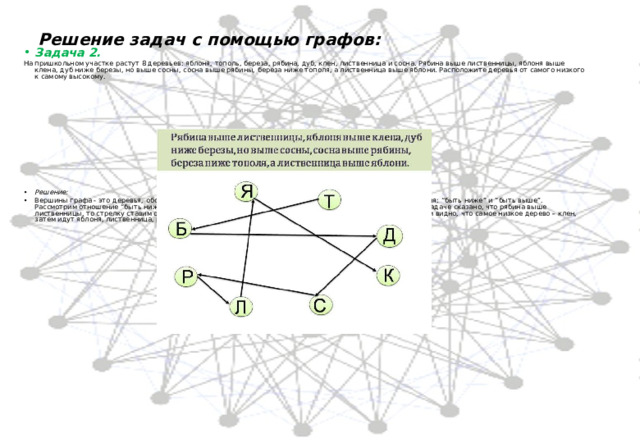
Решение задач с помощью графов:

• Задача 2.

На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.   

• Решение: 
• Вершины графа - это деревья, обозначенный первой буквой названия дерева.  В данной задаче  два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем ориентированный граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

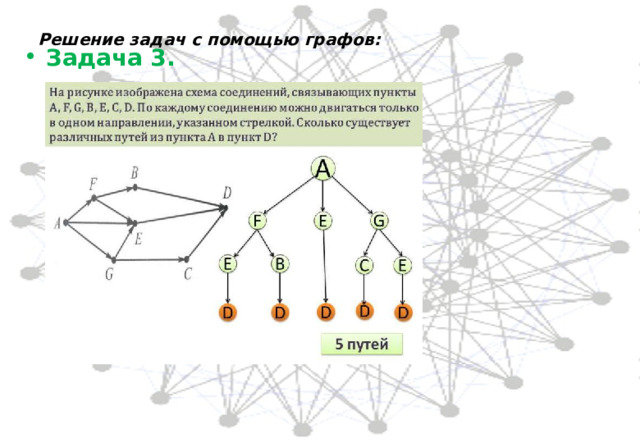
Решение задач с помощью графов:

• Задача 3.

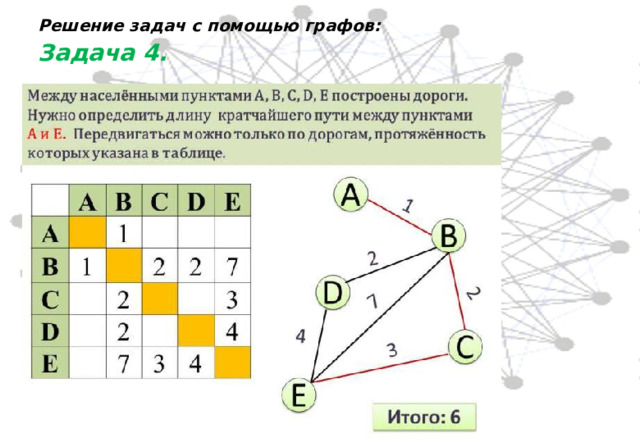
Решение задач с помощью графов: Задача 4.

Задача делового человека Мы предлагаем Вам решить следующую задачу самостоятельно и найти кратчайший путь из Санкт-Петербурга в Омск.

Заключение

Дав основные понятия теории графов и решив несколько задач, мы можем сделать вывод что, выделяя из словесных рассуждений главное – объекты и отношения между ними, графы представляют изучаемые факты в наглядной форме.

Приемы решения логических задач с использованием графов подкупают своей естественностью и простотой, избавляют от лишних рассуждений и, как мы убедились, сокращают нагрузку на память.

Литература:

• Список литературы:
• Генкин С. А., Итенберг И.В., Фомин Д. В. Ленинградские математические кружки: пособие для внеклассной работы. – Киров: АСА, 1994. – 272 с.
• Гуровиц В. М., Ховрина В. В. Графы. – М.: МЦНМО, 2008. – 32 с.: ил.
• Ссылки на интернет- источники:

Решение задач с помощью графа

https://globallab.org/ru/project/cover/reshenie_zadatch_s_pomoshju_grafa.ru.html#.VM-4Q8mE3F0