Графы - информационные модели

Информационные модели на графах

История возникновения графов

• Впервые основы теории графов появились в работах Леонарда Эйлера (1707-1783; швейцарский, немецкий и российский математик ) , в которых он описывал решение головоломок и математических развлекательных задач.
• Теория графов началась с решения Эйлером задачи о семи мостах Кёнигсберга.

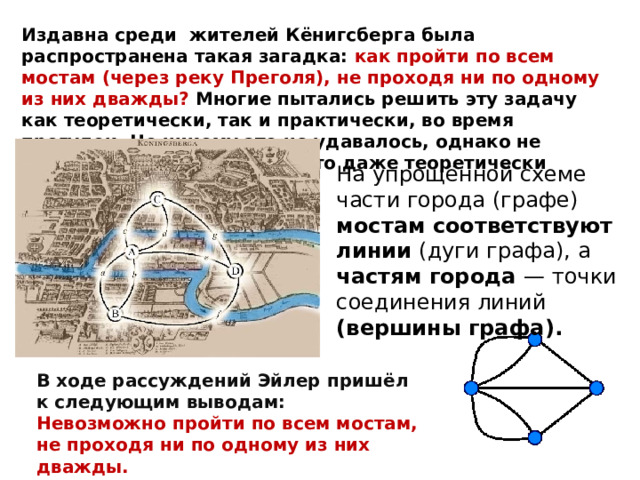
Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды? Многие пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.

На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа).

В ходе рассуждений Эйлер пришёл к следующим выводам: Невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

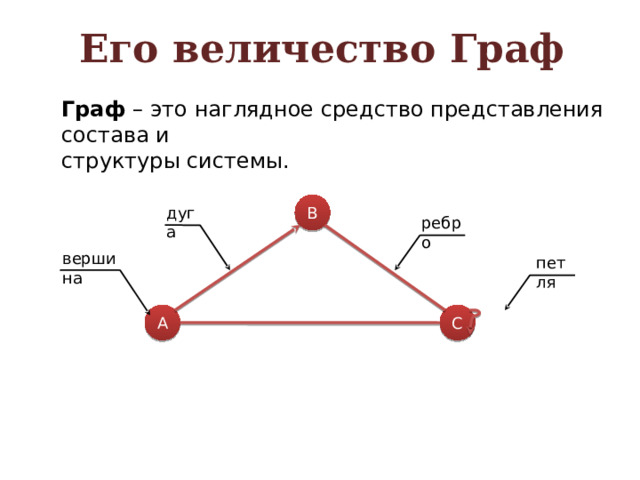
Его величество Граф

Граф – это наглядное средство представления состава и

структуры системы.

В

дуга

ребро

вершина

петля

С

А

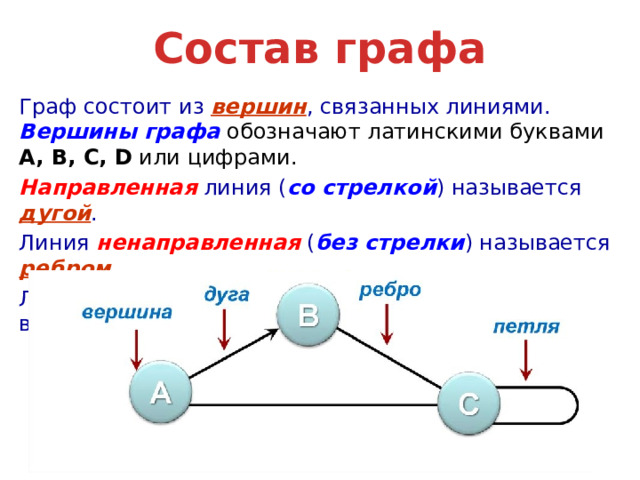
Состав графа

Граф состоит из вершин , связанных линиями. Вершины графа обозначают латинскими буквами A, B, C, D или цифрами.

Направленная линия ( со стрелкой ) называется дугой .

Линия ненаправленная ( без стрелки ) называется ребром .

Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей .

ребро

дуга

В

петля

А

С

5

Неориентированный граф

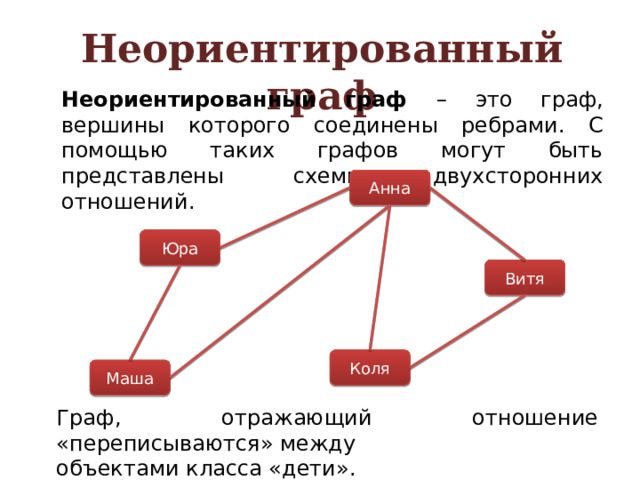
Неориентированный граф – это граф, вершины которого соединены ребрами. С помощью таких графов могут быть представлены схемы двухсторонних отношений.

Анна

Юра

Витя

Коля

Маша

Граф, отражающий отношение «переписываются» между

объектами класса «дети».

Ориентированный граф

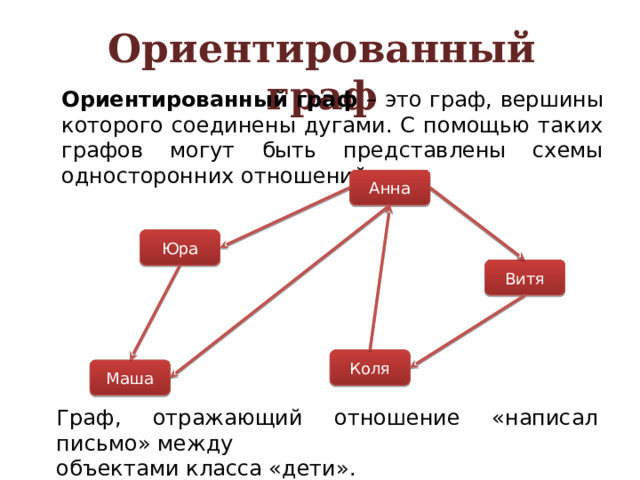
Ориентированный граф – это граф, вершины которого соединены дугами. С помощью таких графов могут быть представлены схемы односторонних отношений.

Анна

Юра

Витя

Коля

Маша

Граф, отражающий отношение «написал письмо» между

объектами класса «дети».

Взвешенный граф

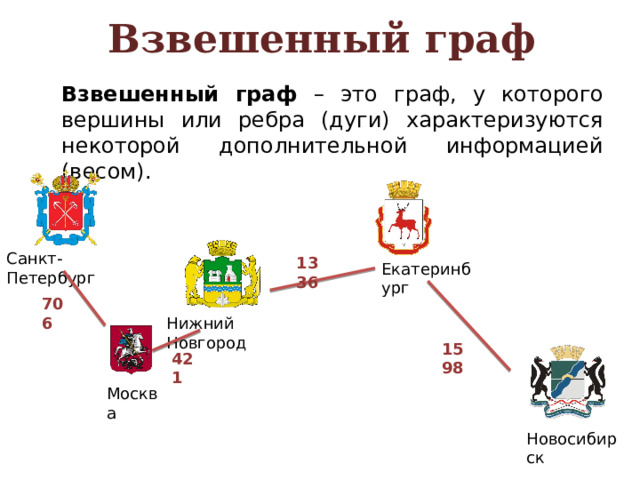
Взвешенный граф – это граф, у которого вершины или ребра (дуги) характеризуются некоторой дополнительной информацией (весом).

Санкт-Петербург

1336

Екатеринбург

706

Нижний Новгород

1598

421

Москва

Новосибирск

Применение графов

С помощью графов упрощается решение математических задач, головоломок, задач на смекалку.

дальше

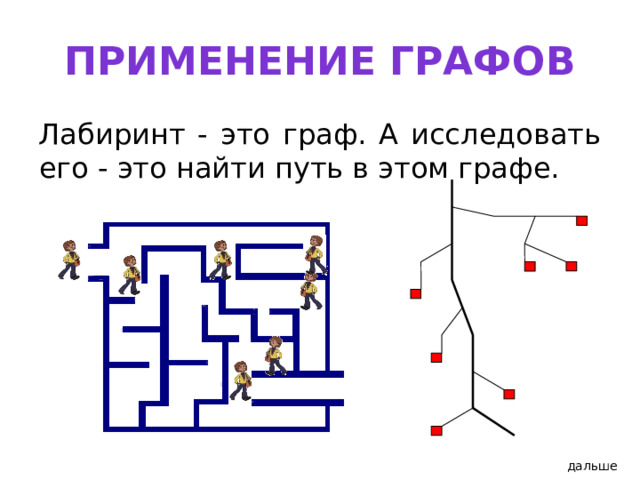
Применение графов

Лабиринт - это граф. А исследовать его - это найти путь в этом графе.

дальше

Применение графов

Использует графы и дворянство.

На рисунке приведена часть генеалогического дерева знаменитого дворянского рода Л. Н. Толстого. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.

дальше

Применение графов

Типичными графами на картах города являются схемы движения городского транспорта .

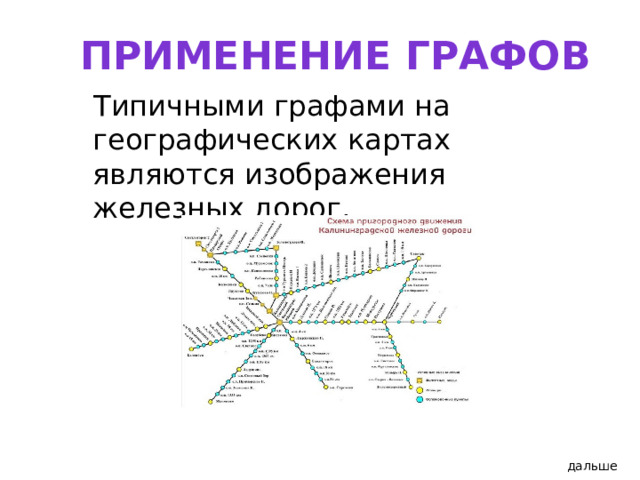
Применение графов

Типичными графами на географических картах являются изображения железных дорог.

дальше

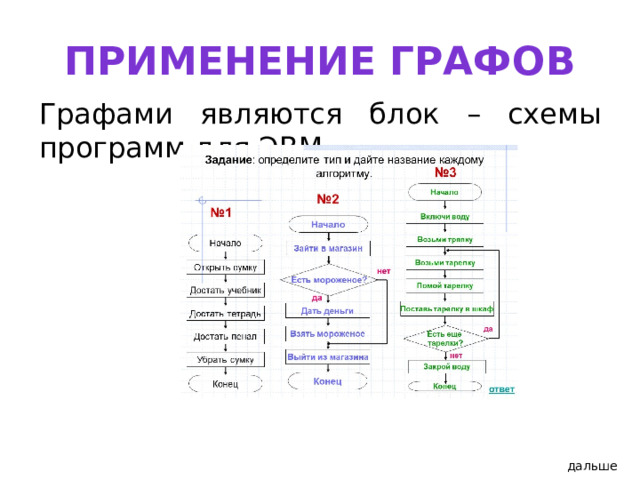
Применение графов

Графами являются блок – схемы программ для ЭВМ.

дальше

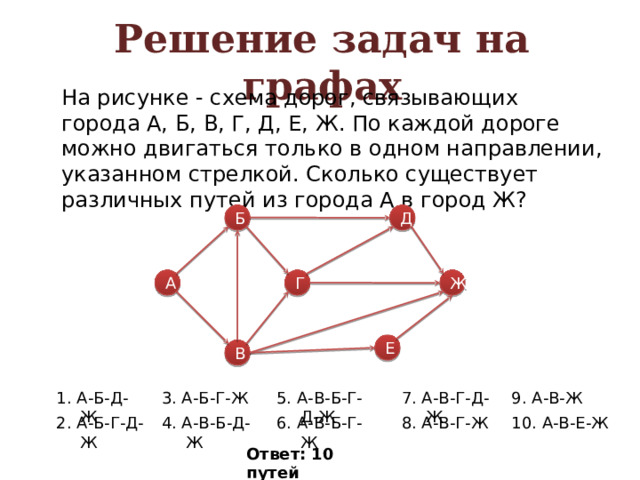
Решение задач на графах

На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Д

Б

Г

Ж

А

Е

В

1. А-Б-Д-Ж

3. А-Б-Г-Ж

5. А-В-Б-Г-Д-Ж

7. А-В-Г-Д-Ж

9. А-В-Ж

2. А-Б-Г-Д-Ж

4. А-В-Б-Д-Ж

6. А-В-Б-Г-Ж

8. А-В-Г-Ж

10. А-В-Е-Ж

Ответ: 10 путей

Решение задач на графах

Ответ 5

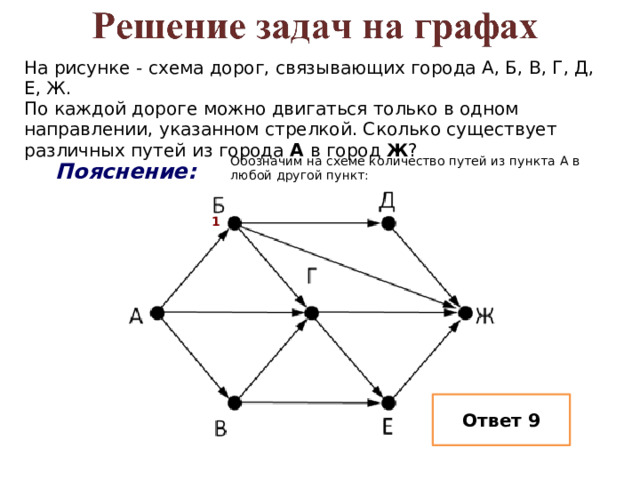
На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж.

По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж ?

Обозначим на схеме количество путей из пункта А в любой другой пункт:

Пояснение:

1

Ответ 9

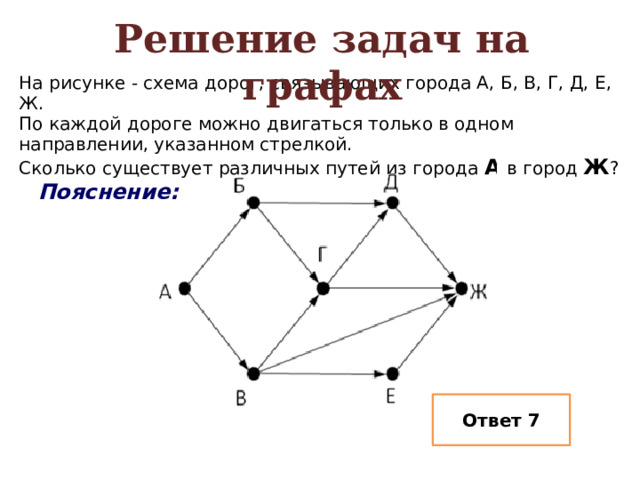
Решение задач на графах

На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж.

По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город Ж ?

Пояснение:

Ответ 7

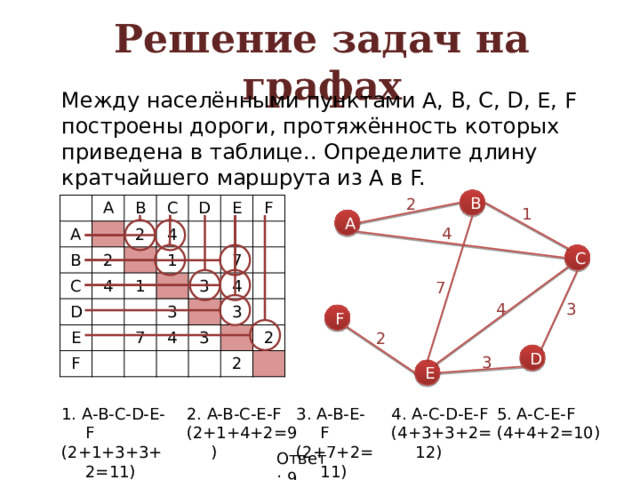
Решение задач на графах

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице.. Определите длину кратчайшего маршрута из А в F.

2

B

А

A

B

B

2

C

2

C

4

4

D

D

E

1

1

E

F

F

7

3

3

7

4

4

3

3

2

2

1

А

4

C

7

3

4

F

2

D

3

E

3. A-B-E-F

5. A-C-E-F

4. A-C-D-E-F

2. A-B-C-E-F

1. A-B-C-D-E-F

(2+1+4+2=9)

(2+7+2=11)

(2+1+3+3+2=11)

(4+3+3+2=12)

(4+4+2=10)

Ответ: 9

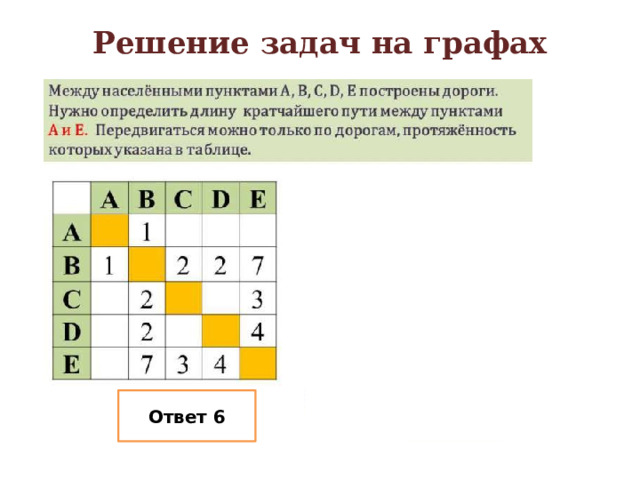
Решение задач на графах

Ответ 6

Решение задач на графах

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Определите длину кратчайшего маршрута из А в Е.

Ответ 9

Решение задач на графах

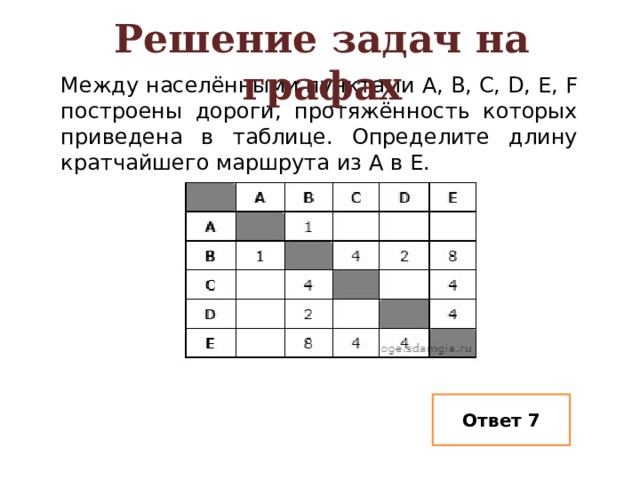
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Определите длину кратчайшего маршрута из А в Е.

Ответ 7

д/з готовимся к сам. работе параграфы 9, 10, 11,13