ГИПЕРБОЛА вокруг нас

Урок на основе исследовательской технологии по теме:

«Функция и ее график»

изотерма

I

Р

T2

T1

R

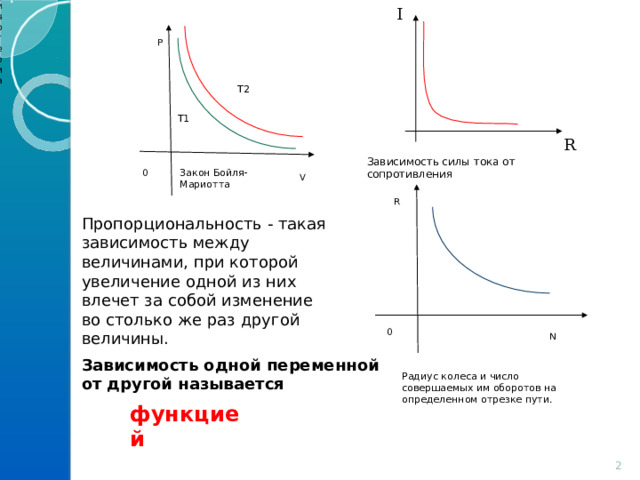
Зависимость силы тока от сопротивления

Закон Бойля-Мариотта

0

V

R

Пропорциональность - такая зависимость между величинами, при которой увеличение одной из них влечет за собой изменение во столько же раз другой величины.

0

N

Зависимость одной переменной от другой называется

Радиус колеса и число совершаемых им оборотов на определенном отрезке пути.

функцией

2

Повторение ранее изученного материала

у

1

0

1

х

Обратной пропорциональностью

называется функция, которую

можно задавать формулой вида

где у – зависимая переменная

х – независимая переменная,

k – не равное нулю число.

4

Функция у=к\х

1. Областью определения функции является

множество всех чисел, отличных от нуля

Так как выражение имеет смысл при всех х = 0

2. Областью значений функции

является

множество всех чисел, отличных от нуля.

Решите задачи

• Пешеход путь S проходит со скоростью v за t часов. Выразите время пешехода через путь и скорость.
• Площадь прямоугольника со сторонами x и y равна S . Выразите у через S и х.
• Площадь прямоугольника со сторонами x и y равна S . Выразите у через S и х.

Как связаны между собой х и у?

В явлениях природы, в человеческой деятельности часто встречаются обратно пропорциональные зависимости между двумя величинами.

Как графиком можно представить эту зависимость?

График обратно пропорциональной функции называется ГИПЕРБОЛА

Термин «функция» в 1664г. ввёл немецкий учёный Лейбниц. Определение функции дал его ученик Бернулли в 1718 году

Одним из первых, кто начал изучать эту кривую был ученик знаменитого Платона, древнегреческий математик Менехм в IV в. до н.э., но так и не сумел её полностью изучить. А вот полностью исследовал свойства гиперболы и дал ей название крупнейший геометр древности Аполоний Пергский в III в. до н.э.

Детально рассмотрим эту зависимость с помощью графика на примере функций у=12/х Как построить график незнакомой нам функции?

Сформулируем памятку построения

• Составить таблицу значений (взять значения аргумента с расчетом, чтобы положение графика определялось с достаточной полнотой).
• Отметить точки на координатной плоскости.
• Соединить точки линией.

0 при х 0; y3. Убывающая функция 4. у - не существует у - не существует наибольшее наименьшее 5. Функция имеет точку разрыва х = 0 6. Область значения функции y  ( - ∞ ;0)  (0;+∞) Анализ графика " width="640"

Х

у

- 1

- 2

- 12

- 6

- 3

- 4

- 4

- 6

- 3

- 12

- 2

- 1

1

2

12

3

6

4

4

6

3

12

2

1

Свойства функции:

у

-8

9

8

-7

-6

7

6

-5

-4

5

4

-3

-2

3

-1

2

0

1

-1

1

-2

-3

2

3

-4

-5

4

5

-6

-7

6

7

-8

8

х

Ветви гиперболы

1. Область определения функции х  ( - ∞ ;0)  (0;+∞)

2. y 0 при х 0; y

3. Убывающая функция

4. у - не существует

у - не существует

наибольшее

наименьшее

5. Функция имеет точку разрыва х = 0

6. Область значения функции y  ( - ∞ ;0)  (0;+∞)

Анализ графика

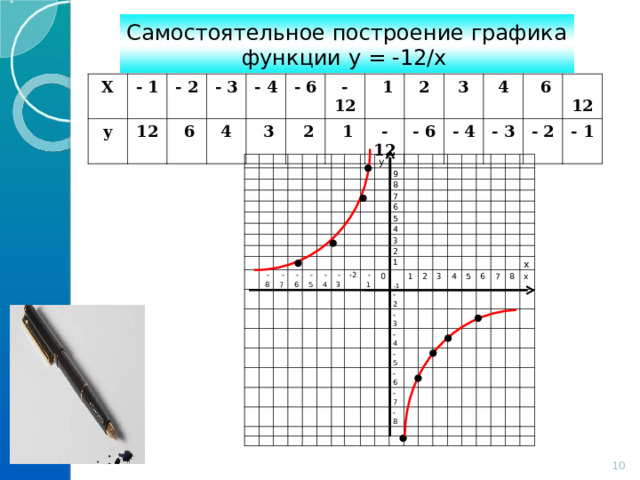
Самостоятельное построение графика функции у = -12/х

Х

у

- 1

- 2

12

- 3

6

- 4

4

3

- 6

2

- 12

1

1

- 12

2

- 6

3

- 4

4

- 3

6

- 2

12

- 1

у

-8

9

-7

8

-6

7

6

-5

-4

5

-3

4

-2

3

-1

2

0

1

-1

1

-2

2

-3

3

-4

4

-5

5

-6

6

-7

7

-8

8

х

х

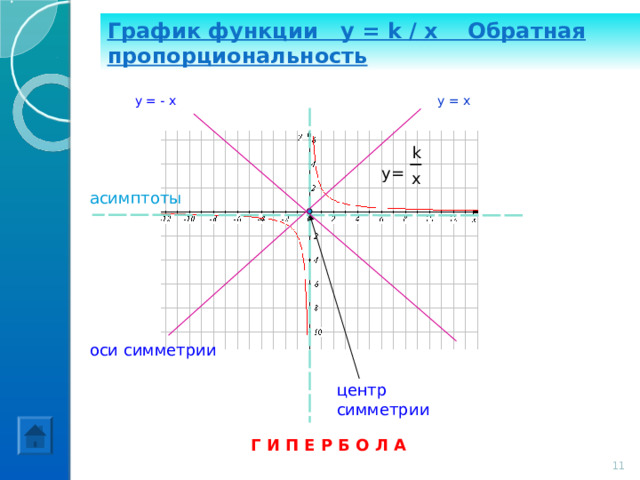
График функции y = k / x Обратная пропорциональность

y = x

y = - x

k

y=

x

асимптоты

оси симметрии

центр симметрии

Г И П Е Р Б О Л А

Самостоятельная работа

• I вариант.

1) В одной координатной плоскости постройте графики заданных функций и найдите координаты

их точек пересечения у = 2х – 3 и . Опишите свойства

функции

• II вариант

1) В одной координатной плоскости постройте графики заданных функций и найдите координаты

их точек пересечения у = х – 2 и

Опишите свойства

функции

• Составить таблицу значений (взять значения аргумента с расчетом, чтобы положение графика определялось с достаточной полнотой).
• Отметить точки на координатной плоскости.
• Соединить точки линией.

Итог урока

• Что является графиком функции

• В каких координатных четвертях расположен график функции?
• Какова область определения функции

• Какими свойствами обладает график функции обратной пропорциональной зависимости?
• Как называется график обратно пропорциональной функции?
• Из чего состоит гипербола?

Укажите какие из функций являются обратной пропорциональностью?

в)

• Из словаря русского языка Ожегова слово гипербола обозначает в поэтике - приём чрезмерного преувеличения с целью усиления впечатления».
• В Большой Российской энциклопедии (т.7) – неправдоподобное преувеличение тех или иных свойств изображения предмета или явления». Например: «…редкая птица долетит до середины Днепра» Н.В. Гоголь.
• Часто гипербола встречается в частушках:

Сидит лодырь у ворот

Широко разинув рот,

И никто не разберёт,

Где ворота, а где рот.

14

• Русский поэт Н.А. Некрасов тоже любил этот прием и применял его в своих стихах. Например:

Пройдёт – словно солнцем осветит:

Посмотрит – рублём подарит!

Я видывал, как она косит

Что взмах – то готова копна.

14

Астрономы всесторонне изучают строение космоса.

Среди тел Солнечной системы много комет. Вблизи Солнца многие кометы движутся по орбитам, близким к гиперболам.

14

Домашнее задание:

• Изучить п.11
• Решить №277, №278, №279, №280.
• Подготовить сообщения на тему «Применение функции в различных областях науки и в литературе» до 20 ноября 2017г.

14