Геометрическая задача на вычисление

Треугольники

1. В пря­мо­уголь­ном тре­уголь­ни­ке с пря­мым углом из­вест­ны ка­те­ты:

, . Най­ди­те ме­ди­а­ну этого тре­уголь­ни­ка.

2. Точка H яв­ля­ет­ся ос­но­ва­ни­ем вы­со­ты BH, про­ведённой из вер­ши­ны пря­мо­го угла B пря­мо­уголь­но­го тре­уголь­ни­ка ABC. Окруж­ность с диа­мет­ром BH пе­ре­се­ка­ет сто­ро­ны AB и CB в точ­ках P и K со­от­вет­ствен­но. Най­ди­те BH, если PK = 20.

3. Точка H яв­ля­ет­ся ос­но­ва­ни­ем вы­со­ты, про­ведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 5, AC = 20.

4. Ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют­ся в точке . Най­ди­те длину ме­ди­а­ны, про­ведённой к сто­ро­не , если угол равен 47°, угол равен 133°, .

5. Окруж­ность про­хо­дит через вер­ши­ны А и С тре­уголь­ни­ка АВС и пе­ре­се­ка­ет его сто­ро­ны АВ и ВС в точ­ках К и Е со­от­вет­ствен­но. От­рез­ки АЕ и СК пер­пен­ди­ку­ляр­ны. Най­ди­те ∠КСВ, если ∠АВС = 20°.

6. 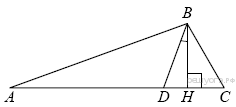В тре­уголь­ни­ке АВС углы А и С равны 20° и 60° со­от­вет­ствен­но. Най­ди­те угол между вы­со­той ВН и бис­сек­три­сой BD.

7. 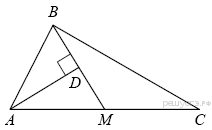Пря­мая AD, пер­пен­ди­ку­ляр­ная ме­ди­а­не ВМ тре­уголь­ни­ка АВС, делит её по­по­лам. Най­ди­те сто­ро­ну АС, если сто­ро­на АВ равна 4.

8. Катет и ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка равны 18 и 30. Най­ди­те вы­со­ту, про­ведённую к ги­по­те­ну­зе.

9. Точка H яв­ля­ет­ся ос­но­ва­ни­ем вы­со­ты BH, про­ведённой из вер­ши­ны пря­мо­го угла B пря­мо­уголь­но­го тре­уголь­ни­ка ABC. Окруж­ность с диа­мет­ром BH пе­ре­се­ка­ет сто­ро­ны AB и CB в точ­ках P и K со­от­вет­ствен­но. Най­ди­те PK, если BH = 16.

10. От­рез­ки AB и DC лежат на па­рал­лель­ных пря­мых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 16, DC = 24, AC = 25 .

11. Окруж­ность пе­ре­се­ка­ет сто­ро­ны AB и AC тре­уголь­ни­ка ABC в точ­ках K и P со­от­вет­ствен­но и про­хо­дит через вер­ши­ны B и C. Най­ди­те длину от­рез­ка KP, если AP = 18, а сто­ро­на BC в 1,2 раза мень­ше сто­ро­ны AB.

12. 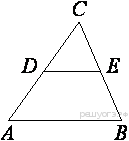В тре­уголь­ни­ке ABC DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 9. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

13. Пря­мая, па­рал­лель­ная сто­ро­не AC тре­уголь­ни­ка ABC, пе­ре­се­ка­ет сто­ро­ны AB и BC в точ­ках M и N со­от­вет­ствен­но. Най­ди­те BN, если MN = 13, AC = 65, NC = 28.

14. Най­ди­те от­но­ше­ние двух сто­рон тре­уголь­ни­ка, если его ме­ди­а­на, вы­хо­дя­щая из их общей вер­ши­ны, об­ра­зу­ет с этими сто­ро­на­ми углы в 30° и 90°.

15. Вы­со­та тре­уголь­ни­ка раз­би­ва­ет его ос­но­ва­ние на два от­рез­ка с дли­на­ми 8 и 9. Най­ди­те длину этой вы­со­ты, если из­вест­но, что дру­гая вы­со­та тре­уголь­ни­ка делит ее по­по­лам.

16. Бис­сек­три­сы углов и при бо­ко­вой сто­ро­не тра­пе­ции пе­ре­се­ка­ют­ся в точке . Най­ди­те , если .

17. В тре­уголь­ни­ке ABC угол С равен 90°, ра­ди­ус впи­сан­ной окруж­но­сти равен 2. Най­ди­те пло­щадь тре­уголь­ни­ка ABC, если AB = 12.

18. В тре­уголь­ни­ке из­вест­но, что - сред­няя линия. Пло­щадь тре­уголь­ни­ка равна 25. Най­ди­те пло­щадь тре­уголь­ни­ка .

19. Ме­ди­а­на BM и бис­сек­три­са AP тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке K, длина сто­ро­ны AC от­но­сит­ся к длине сто­ро­ны  AB как 7:10. Най­ди­те от­но­ше­ние пло­ща­ди тре­уголь­ни­ка AKM к пло­ща­ди тре­уголь­ни­ка ABC.

20. Точка H яв­ля­ет­ся ос­но­ва­ни­ем вы­со­ты BH, про­ведённой из вер­ши­ны пря­мо­го угла B пря­мо­уголь­но­го тре­уголь­ни­ка ABC. Окруж­ность с диа­мет­ром BH пе­ре­се­ка­ет сто­ро­ны AB и CB в точ­ках P и K со­от­вет­ствен­но. Най­ди­те PK, если BH = 11.