Функцияның өсу және кему белгілері. Функцияның кризистік нүктелері мен экстремумдары. Функция графигінің дөңестігі мен ойыстығы. Иілу нүктелері.

Сабақтың тақырыбы: Функцияның өсу және кему белгілері. Функцияның кризистік нүктелері мен экстремумдары. Функция графигінің дөңестігі мен ойыстығы. Иілу нүктелері.

Тема урока: Признаки возрастания и убывания функции. Кризисные точки и экстремумы функции. Выпуклость и вогнутость графика функции. Точки перегиба.

Функцияның өсу және кему Возрастание и убывание функции

Таудан түскен кезде. Функция [a; с] кемейді.

Көтерілу тауға. Функция [b; а] интервалында өседі.

Подняться на гору. Функция возрастает на интервале [b; a]

При спуске с горы. Функция убывает на интервале [a; c]

y

a

b

c

x

0

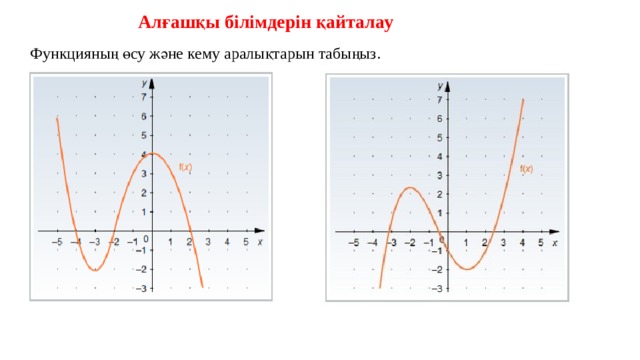
Алғашқы білімдерін қайталау

Функцияның өсу және кему аралықтарын табыңыз.

функция графигі

және оның туындысы

арасындағы байланысты қарастырайық.

Рассмотрим связь между

графиком функции

и ее производной

Қорытындылар: Выводы:

• Функцияның туындысының графигі Ох осінен жоғары орналасқан x нүктелерінің жиынтығы функцияның графигі өсетін x нүктелерінің жиынына сәйкес келеді.
• Функцияның туындысының графигі Ох осінен төмен орналасқан x нүктелерінің жиынтығы функцияның графигі төмендейтін x нүктелерінің жиынына сәйкес келеді.

1. Множество точек х , где график производной функции располагается выше оси О х , соответствует множеству точек х , где график функции возрастает.

2. Множество точек х , где график производной функции располагается ниже оси О х , соответствует множеству точек х , где график функции убывает.

0), онда бұл аралықта функция өседі. Теорема 2: Егер f(x) кейбір үздіксіз функциясының туындысы кейбір аралықта теріс болса (f'(x)" width="640"

Функцияның аралықта өсуінің (кемуінің) қажетті және жеткілікті шарттары

Теорема 1: Егер f(x) кейбір үздіксіз функциясының туындысы кейбір аралықта оң болса (f'(x)0), онда бұл аралықта функция өседі.

Теорема 2: Егер f(x) кейбір үздіксіз функциясының туындысы кейбір аралықта теріс болса (f'(x)

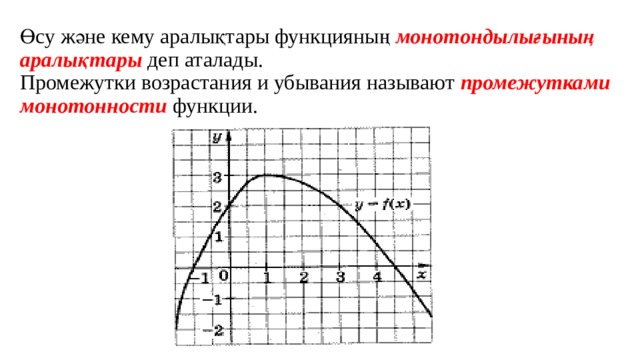
Өсу және кему аралықтары функцияның монотондылығының аралықтары деп аталады. Промежутки возрастания и убывания называют промежутками монотонности функции.

Монотондық аралықтарды табу реті:

• Функцияның анықталу облысын табыңыз.
• Функцияның бірінші туындысын табыңыз.
• Кризистік нүктелерін тауып, бірінші ретті туындының таңбасын зерттеңіз.
• Жауабын жазыңыз.

Мысалы: Функцияның монотондық аралықтарды табыңыз:

• анықталу облысы D ( y ): x ∈ R
• бірінші ретті туынды y ′=,
• кризистік нүктелер  y ′=0; =0, x =0  и  x =2    

Бірінші ретті туындының таңбасын зерттейміз

x ∈(−∞;0)∪(2;+∞) функция өседі,   х ∈(0;2) кемиді.

0 или f / (x) 4. Записать промежутки возрастания и убывания функции. " width="640"

Алгоритм нахождения промежутков монотонности

• Найти область определения функции.
• Найти производную функции.

3. Решить неравенства f / (x) 0 или f / (x)

4. Записать промежутки возрастания и убывания функции.

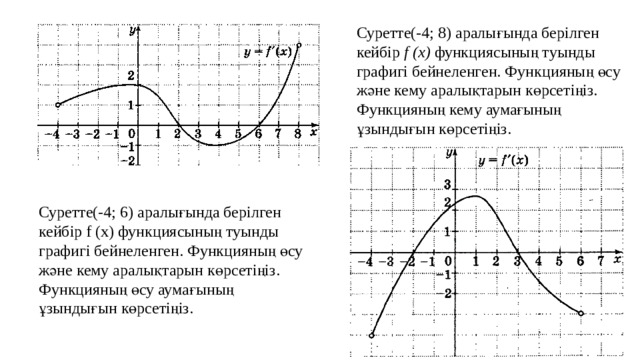
Суретте(-4; 8) аралығында берілген кейбір f (x) функциясының туынды графигі бейнеленген. Функцияның өсу және кему аралықтарын көрсетіңіз. Функцияның кему аумағының ұзындығын көрсетіңіз.

Суретте(-4; 6) аралығында берілген кейбір f (x) функциясының туынды графигі бейнеленген. Функцияның өсу және кему аралықтарын көрсетіңіз. Функцияның өсу аумағының ұзындығын көрсетіңіз.

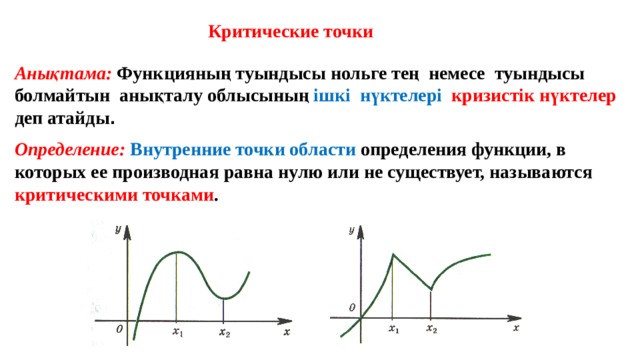
Критические точки

Анықтама: Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері кризистік нүктелер деп атайды .

Определение: Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками .

Қажетті шарты

Егер f(x) функциясының х экстремум нүктесі болып және оны осы нүктенің аймағында f’(x ) туындысы бар болса , онда ол туынды х нүктесінде нөлге тең , яғни f’(x )=0

0 (f’(x)0 ) болса , онда х нүктесінде f(x) функцияның максимум (минимум) нүктесі болады. " width="640"

Жеткілікті шарты

• Егер х нүктесінде f(x) функциясы үзіліссіз, ал (а;х ) аралығында f’(x)0 (f’(x)0 ) болса , онда х нүктесінде f(x) функцияның максимум (минимум) нүктесі болады.

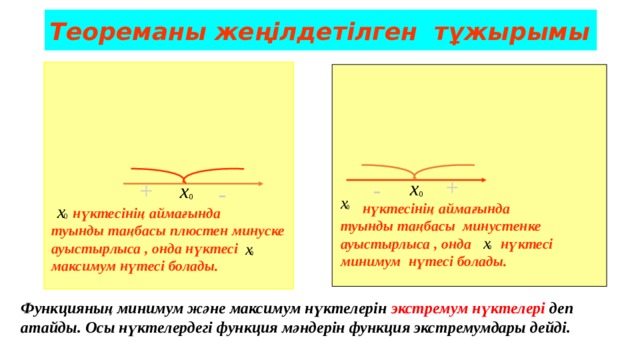
Теореманы жеңілдетілген тұжырымы

+

-

+

-

нүктесінің аймағында

туынды таңбасы минустенке ауыстырлыса , онда нүктесі минимум нүтесі болады.

нүктесінің аймағында

туынды таңбасы плюстен минуске ауыстырлыса , онда нүктесі

максимум нүтесі болады.

Функцияның минимум және максимум нүктелерін экстремум нүктелері  деп атайды. Осы нүктелердегі функция мәндерін функция экстремумдары дейді.

Функцияның экстремум нүктелерін табу алгоритмін тұжырымдаңыз

• 1. функцияның туындысын табу;
• 2.функцияның кризистік нүктелерін табу, яғни f’(x)=0 теңдеуін шешу және туындының анықталмайтын нүктелерін табу.
• 3. кризистік нүктелер аймағында f’(x) тыундының таңбасын анықтау;
• 4.экстремум нүтелерінің бар болуының жеткілікті шартын ,қолданып максимум және минимум нүктелерін табу.

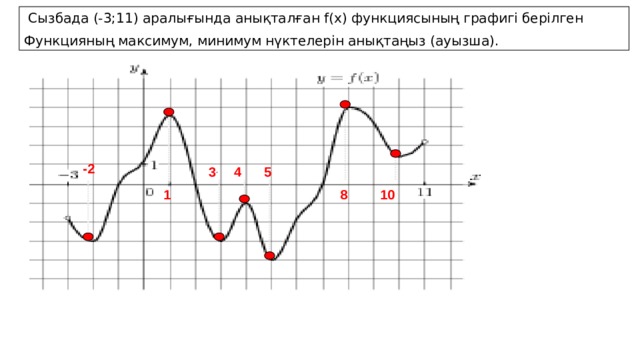
Сызбада (-3;11) аралығында анықталған f(x) функциясының графигі берілген

Функцияның максимум, минимум нүктелерін анықтаңыз (ауызша).

-2

5

4

3

.

8

10

1

f(х 0 ). Обозначается : Xmin, а значение функции в этой точке – Ymin ( не путать с Унаим). Точки минимума и точки максимума вместе называются точками экстремума . " width="640"

Точки экстремума

• Точка х 0 называется точкой максимума функции f(x) , если существует такая окрестность точки х 0 , что для всех х (кроме х 0 ) из этой окрестности выполняется неравенство f(x)

Обозначается : Xmax, а значение функции в этой точке – Ymax ( не путать с Унаиб).

• Точка х 0 называется точкой минимума функции f(x) , если существует такая окрестность точки х 0 , что для всех х (кроме х 0 ) из этой окрестности выполняется неравенство f(x) f(х 0 ).

Обозначается : Xmin, а значение функции в этой точке – Ymin ( не путать с Унаим).

Точки минимума и точки максимума вместе называются точками экстремума .

0 , а на интервале (х 0 ,b) f'(x) , то точка х 0 является точкой максимума функции f Признак минимума функции Если функция f в точке х 0 непрерывна и на интервале (а, х 0 ) f'(x) , а на интервале (х 0 ,b) f'(x) 0 , то точка х 0 является точкой минимума функции f + х 1 - х 2 + х 3 - max min max f'(x) f(x) " width="640"

Если функция имеет экстремум в точке , то производная функции либо равна нулю, либо не существует

Точки минимума и максимума функции называют точками экстремума.

Значения функции в этих точках называют экстремумами функций . 

Признак максимума функции

Если функция f в точке х 0 непрерывна и на интервале (а, х 0 ) f'(x) 0 , а на интервале (х 0 ,b) f'(x) , то точка х 0 является точкой максимума

функции f

Признак минимума функции

Если функция f в точке х 0 непрерывна и на интервале (а, х 0 ) f'(x) , а на интервале (х 0 ,b) f'(x) 0 , то точка х 0 является точкой минимума

функции f

+ х 1 - х 2 + х 3 -

max min max

f'(x)

f(x)

План исследования функции на экстремум:

1.     Найти область определения функции. 2.     Найти производную. 3.     Найти критические точки, в которых производная равна нулю или

не существует. Расположить их в порядке возрастания. 4.     Исследовать знак производной в полученных промежутках. 5.     Вычислить значение функции в точках максимума и минимума.

 0болса ,онда   (  a ,  b  )аралығында    f  (  x  ) функциясы дөңес (ойыс  )төмен ,  ал егер     кез келген   x    (  a ,  b  )үшін f  (  x  )  ''  (  x  ) a ,  b  )аралығында    f  (  x  ) функциясы дөңес (ойыс  )жоғары болады .  .   Функцияның дөңестен ойысқа немесе керісінше ауысатын нүктесін иілу нүктесі деп атайды. Осыдан    x 0 иілу нүктесінде функцияның екінші ретті туындысы бар    f ''  (  x 0  ), онда    f ''  (  x 0  ) = 0. " width="640"

  f  (  x  ) функциясы (  a ,  b  )аралығында ,    жоғары дөңес (ойыс ) деп аталады  егер оның графигі осы аралықта y = f  (  x) қисығына кез келген   x 0   ,   f  (  x 0  )),   x 0   (  a ,  b  )нүктелерінен

жүргізілген жанамадан төмен болса.      f  (  x  ) функциясы (  a ,  b  )аралығында ,   төмен дөңес (ойыс ) деп аталады  егер оның графигі осы аралықта y = f  (  x) қисығына кез келген   x 0   ,   f  (  x 0  )),   x 0   (  a ,  b  )нүктелерінен

жүргізілген жанамадан жоғары болса.   

Функцияның дөңес (ойыс  )- тығының жеткілікті шарты .

  (  a ,  b  ) аралығында   f  (  x  ) функциясының екінші ретті туындысы болсын  онда :

Егер     кез келген   x    (  a ,  b  )үшін f ''  (  x  )  0болса ,онда   (  a ,  b  )аралығында    f  (  x  ) функциясы дөңес (ойыс  )төмен ,  ал егер     кез келген   x    (  a ,  b  )үшін f  (  x  )  ''  (  x  ) a ,  b  )аралығында    f  (  x  ) функциясы дөңес (ойыс  )жоғары болады .  .

 

Функцияның дөңестен ойысқа немесе керісінше ауысатын нүктесін иілу нүктесі деп атайды. Осыдан    x 0 иілу нүктесінде функцияның екінші ретті туындысы бар    f ''  (  x 0  ), онда    f ''  (  x 0  ) = 0.

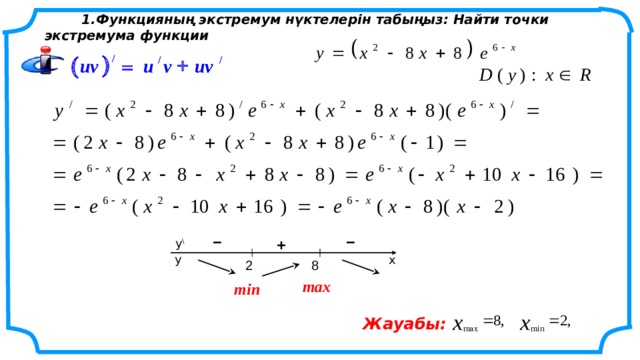
1.Функцияның экстремум нүктелерін табыңыз: Найти точки экстремума функции

)

(

/

+

/

/

=

v

uv

uv

u

–

–

+

y \

y

x

2

8

max

min

Жауабы:

1. Өсу және кему аралықтарын табыңыз:

A

 

.

B

 

Үй жұмысы. Домашняя работа.

Функцияның өсу және кему аралықтарын табыңыз :

Найдите промежутки возрастания и убывания функции:

 

.