Функцию y=x2 называют квадратной функцией.
График функции y=x2 называется параболой.
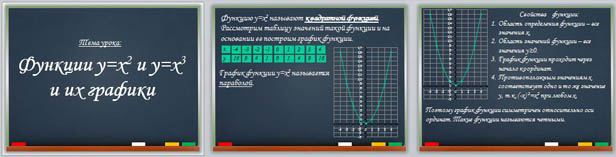
Свойства функции:
2. Область значений функции – все значения y≥0.
4. Противоположным значениям x соответствует одно и то же значение y, т.к. (-x) 2=x2 при любом x.
Поэтому график функции симметричен относительно оси ординат. Такие функции называются четными.
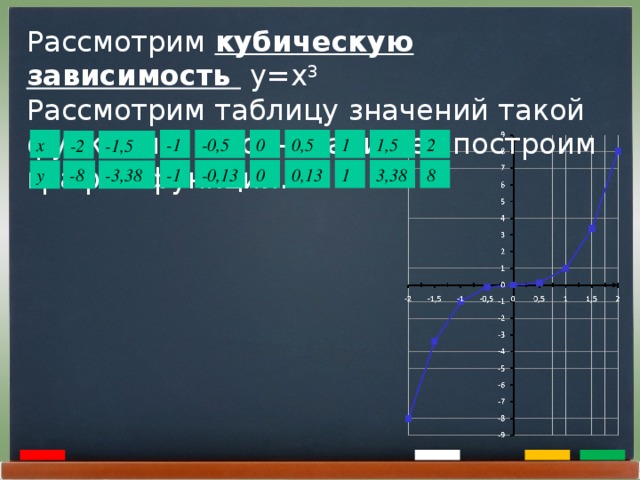
Рассмотрим кубическую зависимость y=x3
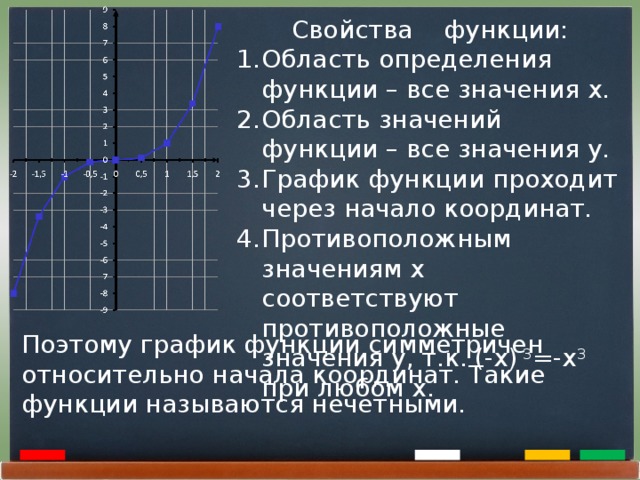
Свойства функции:
2. Область значений функции – все значения y.
4. Противоположным значениям x соответствуют противоположные значения y, т.к. (-x) 3=-x3 при любом x.
Поэтому график функции симметричен относительно начала координат. Такие функции называются нечетными.

 Получите свидетельство
Получите свидетельство Вход
Вход













 Функции y=x2 и y=x3 и их графики (1.03 MB)
Функции y=x2 и y=x3 и их графики (1.03 MB)
 1
1 1848
1848 455
455 Нравится
0
Нравится
0



