Тема работы
«Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе».
Тема работы «Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе».
Цель работы – систематизировать приемы и методы развития навыков самостоятельной деятельности учащихся, в наибольшей степени отвечающие моим индивидуальным особенностям и особенностям учащихся в данном классе, по данной теме, позволяющие своевременно обнаружить и ликвидировать ошибки и недочеты по основным школьным темам курса алгебры и геометрии.
Задачи работы.
1. Определить уровень сформированности навыков самостоятельной работы на уроках математики.
2. Определить систему упражнений по формированию навыков самостоятельной работы у учащихся при изучении математики.
3.сформировать у учащихся навыки самостоятельной деятельности, приобщение к самообразованию, формирование потребности в систематическом и самостоятельном добывании знаний, пополнении умений.
Объект работы.
Самостоятельная деятельность школьника на уроках математики.
Предмет работы.
Условия реализации самостоятельной деятельности школьника на уроках математики.
Гипотеза работы.
Реализация самостоятельной деятельности учащихся на уроках математики будет более эффективна при организации следующих педагогических условий:
- прививать школьникам навыки выполнения самостоятельной работы;
- использовать на уроках различные виды самостоятельной работы.
Тогда у детей вырабатывается самостоятельность и развивается мышление, они стремятся выполнять более трудные задания.
План работы
Введение 3 – 4
Организация самостоятельной
деятельности учащихся 4 – 5
Анализ подходов к определению понятия
«самостоятельная работа» 5 – 6
Виды самостоятельной деятельности
учащихся 6 - 7
Технология организации самостоятельной
деятельности учащихся 7 – 14
Цели, задачи и функции самостоятельной
деятельности учащихся 14 – 16
Результативность 16 – 18
Заключение 18 – 19
Литература 20
Приложения.
1.Введение.
Современная педагогическая наука приоритетным направлением развития школы определяет гуманистический подход в организации процесса обучения. Ведущим принципом гуманистической модели учебного процесса является развитие личности школьника. Степень развития ученика измеряется и оценивается его способностью самостоятельно приобретать новые знания и использовать их в учебной и практической деятельности. Существующая сегодня система общего образования не носит еще подлинно гуманистический характер. В связи с этим не в полной мере школа способствует развитию и саморазвитию учащихся, готовит к творческому выполнению всех функций в новом обществе.
Среди факторов, способствующих формированию творческой активности учащихся, одно из ведущих мест занимает самостоятельная деятельность. Только целенаправленная систематическая самостоятельная работа каждого школьника позволяет глубоко усвоить знания, выработать и закрепить умения, превратить их в соответствующие навыки умственного труда.
Актуальность темы.
Ведущим принципом построения современной образовательной системы является дифференциация образования, ставшая средством решения задачи удовлетворения интересов, склонностей и потребностей учащихся, стимулом развития их творческой активности. В последнее время отмечается тенденция увеличения числа школ и классов гуманитарного направления. В этих условиях имеет место ослабление интереса учащихся к предметам математического цикла.
Поэтому главным принципом работы учителя математики является организация деятельности школьников, направленной на формирование не только предметных знаний и умений, но и на развитие самостоятельности и творческой активности учащихся.
Значительный вклад в развитие теории самостоятельности и творческой активности учащихся в процессе обучения внесли видные педагоги Бабанский Ю.К., Данилов М.А., Скаткин М.Н. и др.; психологи Богоявленский Д.Н., Выготский Л.С., Гальперин П.Я., Давыдов В.В., Занков Л.В. и др. Эти исследования показали, что одним из эффективных средств развития самостоятельности и творческой активности учащихся является самостоятельная работа.
Дрозина В.В. сформулировала основные положения теории и практики организации творческой самостоятельной деятельности учащихся. Сущность понятия "самостоятельная работа", цели, задачи, дидактические принципы, функции самостоятельной работы, формы и методы ее организации в процессе обучения полно и глубоко проанализированы в исследованиях: Гарунова М.Г., Королькова Б.Е., Нильсона О.А., Орловского В и др.
Актуальность данной проблемы бесспорна, так как знания, умения, убеждения, духовность нельзя передать от преподавателя к учащемуся, прибегая только к словам. Этот процесс включает в себя знакомство, восприятие, самостоятельную переработку, осознание и принятие этих умений и понятий. Данная проблема актуальна для современной школы, потому что она ещё не достаточно разработана, не изучена до конца.
Ребенок, в первый раз переступающий порог школы, не может еще самостоятельно ставить цель своей деятельности, не в силах еще планировать свои действия, корректировать их осуществление, соотносить полученный результат с поставленной целью, следовательно, эта проблема актуальна и для общества в целом.
В процессе обучения математике задача учителя состоит не только в том, чтобы обеспечивать прочные знания, предусмотренные программой, но и в том, чтобы развивать самостоятельность и активность мышления учащихся.
Самостоятельная работа - это такая познавательная учебная деятельность, когда последовательность мышления ученика, его умственные и практические операции и действия зависят и определяются самим учеником. Присутствие самостоятельной работы необходимо на уроках, в том числе и на уроках математики, так как они тренируют волю, воспитывают работоспособность, внимание, дисциплинируют учащихся. Учителю на уроках математики необходимо опираться на самостоятельную работу учеников, самостоятельное рассуждение, умозаключение.
Самостоятельная работа - это метод, который очень помогает учителю для выяснения способностей учащихся. Работая самостоятельно, ученик должен постепенно овладеть такими общими приемами самостоятельной работы как представление цели работы ее выполнение, проверка, исправление ошибок.
Проблема исследования.
Проблема исследования обусловлена противоречиями:
- между обязательным уровнем математической подготовки, зафиксированным в программе по математике и не способностью учащегося достичь определенного достаточно высокого уровня самостоятельности, открывающего возможность справиться с разными заданиями, добывать новое в процессе решения математических задач.
- между отсутствием в методике математики обобщенного подхода и рекомендаций по организации системы самостоятельных работ и программой, предусмотренной для изучения математики;
- между минимальным уровнем обязательных требований к учащимся и стремлением к более полному раскрытию математических способностей школьников.
2. Организация самостоятельной деятельности учащихся.
Современная дидактика основана на принципе, согласно которому учащиеся должны овладеть основами систематических знаний, определенными умениями и навыками как в результате самостоятельной деятельности, организуемой учителем и ориентированной на содержание учебных программ, так и в процессе восприятия части информации в готовом виде. Иными словами, утверждается руководящая роль учителя в процессе обучения, но одновременно признается и важное значение самостоятельной работы учащихся по овладению учебным материалом.
Реализуя в своей работе основные цели образования и воспитания, учитель решает многие задачи, в частности
-знакомство учеников с основами систематизированных знаний о природе, обществе, технике и культуре в объеме , который позволит им понять основные явления, события и процессы действительности, формирование научного мировоззрения
-обеспечение развития способностей и познавательных интересов учащихся (критическое мышление, внимание, абстрактное мышление, память, разнообразие практических умений), дифференцированный подход к обучению
-приобщение школьников к самообразованию, формирование потребности в систематическом и самостоятельном добывании знаний, пополнении знаний
-систематическое осуществление учащимися самоконтроля и самооценки своей учебной деятельности, включение этих действий в школьную систему контроля и оценки результатов обучения
- практическая и прикладная направленность процесса обучения и т.д.
Непременным условием высокой результативности современного математического образования является активная самостоятельная работа учащихся по обучению математике, ее основных идей и методов, ее практического приложения. Такая работа способствует формированию активной жизненной позиции школьников. Поэтому последние несколько лет я работала над темой «Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе».
ой
Всем известно, что под самостоятельной работой учеников, обычно понимают любую организованную учителем активную деятельность учащихся, направленную на выполнение поставленной дидактической цели, в специально отведённое для этого время: поиск знаний, их осмысление, закрепление и развитие умений и навыков, обобщение и систематизация знаний. Таким образом, не всякую практическую работу можно назвать самостоятельной. Перед самостоятельными работами ставится цель формировать самостоятельность учащихся, научить их самостоятельно приобретать знания, творчески мыслить.
Анализ подходов к определению понятия «самостоятельная работа»
Изучение вопроса самостоятельности началось еще в древности. Аристосен, Сократ, Платон, Аристотель глубоко и всесторонне обосновали в своих трудах значимость добровольного, активного и самостоятельного овладения ребенком знаниями. При этом они исходили из того, что развитие мышления человека может успешно протекать только в процессе самостоятельной деятельности, а совершенствование личности и развитие ее способности - путем самопознания. Такая деятельность доставляет ребенку радость и удовлетворение и тем самым устраняет пассивность с его стороны в приобретении новых знаний. Свое дальнейшее развитие идея о самостоятельности в обучения получает в высказываниях Франсуа Рабле, Мишеля Монтеня, Томаса Мора, которые в эпоху мрачного средневековья в разгар процветания в практике работы школы схоластики, догматизма и зубрежки требуют обучать ребенка самостоятельности воспитывать в нем вдумчивого, критически мыслящего человека. Те же мысли развиваются на страницах педагогических трудов Я.А. Каменского, Ж.Ж. Руссо, И.Г. Песталоцци и др.
В педагогической же литературе самостоятельность учащихся как один из ведущих принципов обучения рассматривается с конца ХVIII века. Вопрос о развитии самостоятельности и активности учащихся - центральный в педагогической системе К. Д. Ушинского, который обосновал пути и средства организации самостоятельной работы учащихся с учетом возрастных периодов обучения.
В 20-х годах ХХ века определенную роль в развития теория самостоятельности учащихся сыграли комплексное обучение и другие формы индивидуализации обучения.
Один из ведущих педагогов Пидкасистый П. И. в своей работе «Самостоятельная познавательная деятельность школьников в обучении» он рассматривает следующее определение: «самостоятельная работа - это не форма организации учебных занятий и не метод обучения. Её правомерно рассматривать скорее как средство вовлечения учащихся в самостоятельную познавательную деятельность, средство ее логической и психологической организации».
В педагогическом же энциклопедическом словаре приводится следующая дефиниция: «Самостоятельная работа учащихся, индивидуальная или коллективная учебная деятельность, осуществляемая без непосредственного руководства учителя». На наш взгляд, данное определение не является достаточно полным. Оно не раскрывает сущностных характеристик данного понятия и требует значительных уточнений.
Педагог-психолог Зимняя И.А. определяет, что самостоятельная работа школьника есть следствие правильно организованной его учебной деятельности на уроке, что мотивирует самостоятельное её расширение, углубление и продолжение в свободное время. Для учителя это означает чёткое осознание не только своего плана учебных действий, но и осознанное его формирование у школьников как некоторой схемы освоения учебного предмета в ходе решения новых учебных задач. Но в целом это параллельно существующая занятость школьника по выбранной им из готовых программ или им самим выработанной программе усвоения какого-либо материала. При этом самостоятельная работа - это высшая форма учебной деятельности школьника, форма самообразования, связанная с его работой в классе.
Такие различные аспекты проблемы самостоятельной работы учащихся исследовались Б. П. Есиповым, М. А. Даниловым, М. Н. Скаткиным, И. Я. Лернером, Н. А. Полоеноковой, А. В. Усовой и др. Однако мнения ученых о сущности самостоятельной работы расходятся. Одни определяют её через понятие «метод обучения», другие - через систему приемов учения.
Так, самостоятельная работа - это такая работа, которая выполняется без непосредственного участия учителя, но по его заданию, в специально предоставленное для этого время, при этом учащиеся, сознательно стремятся достигнуть поставленные цели, употребляя свои усилия и выражая в той или иной форме результат умственных или физических (либо тех и других вместе) действий.
Именно самостоятельная работа вырабатывает высокую культуру умственного труда, которая предполагает не только технику чтения, изучение книги, ведение записей, а, прежде всего, потребность в самостоятельной деятельности, стремление вникнуть в сущность вопроса, идти вглубь ещё не решённых проблем. В процессе такого труда наиболее полно выявляются индивидуальные способности школьников, их наклонности и интересы, которые способствуют развитию умения анализировать факты и явления, учат самостоятельному мышлению, которое приводит к творческому развитию и созданию собственного мнения, своих взглядов, представлений, своей позиции.
Некоторые же ученые рассматривают самостоятельную работу как средство развития обобщенных умений, познавательной самостоятельности, творческой активности и социализации личности, связывают её со способностью к самоорганизации (Г.Н. Алова, З.А. Вологодская, А.А.Дикая, М.Е. Дуранов, В.М. Железяко, В.А. Козаков, В.Я. Ляудис, В.П. Чихачев и др.).
По нашему мнению, наиболее полное определение самостоятельной работы дается В. И. Андреевым. Его точка зрения обусловливается тем, что в процессе самостоятельной работы учащихся могут быть применены самые разнообразные методы и приемы обучения, и поэтому, по его мнению, подводить самостоятельную работу под понятие «метод» в качестве родового понятия некорректно. Также он считает, что понятие «средство» является не основным, а лишь вспомогательным, частным признаком и не может быть взято за родовое понятие.
Таким образом, самостоятельная работа учащихся - это форма организации их учебной деятельности, осуществляемая под прямым или косвенным руководством преподавателя, в ходе которой учащиеся преимущественно или полностью самостоятельно выполняют различного вида здания с целью развития знаний, умений, навыков и личных качеств.
4.Виды самостоятельной деятельности учащихся.
Основная цель моей работы – найти приемы и методы, в наибольшей степени отвечающие моим индивидуальным особенностям и особенностям учащихся в данном классе по данной теме, позволяющие своевременно обнаружить и ликвидировать ошибки и недочеты по основным темам курса алгебры и геометрии.
В своей работе я стараюсь изжить устаревший взгляд на самостоятельную работу как на работу, связанную исключительно с закреплением, повторением изученного и с контролем за усвоением. Стараюсь использовать разнообразные виды самостоятельной работы для активизации учебной деятельности школьников, воспитание у них активности, самостоятельности мышления, умения применять знания в процессе обучения. Остановлюсь на тех приемах, которые я применяю чаще других.
Самостоятельная работа на этапе проверки домашнего задания и повторения.
Устные упражнения на уроках.
Работы, подготавливающие учеников к изучению нового материала.
Математические диктанты.
Устные контрольные работы.
Обучающие самостоятельные работы.
Контролирующие самостоятельные работы.
Самостоятельное приобретение знаний и умений (работа с книгой).
Зачеты.
Таблицы.
Учебный проект.
5.Технология организации самостоятельной деятельности учащихся
А)Самостоятельная работа на этапе проверки домашнего задания и повторения.
Самостоятельная работа по домашнему заданию, включающая в себя и домашние задания и задания, подобные им, носит контролирующий характер, помогает выяснить качество подготовки учащихся к уроку. Так же контроль за усвоением изученного обычно начинаю с проверки домашнего задания. Её можно осуществлять в разных формах. Перечисляю некоторые из них, которые я применяю.
а) Самопроверка по образцу.
б) Взаимопроверка по образцу.
в) Проверка домашнего задания консультантами.
г) Проверка - консультация.
д) Опрос по парам.
е) Математическая викторина.
ж) Теоретическая разминка.
Б)Устные упражнения на уроках.
Правильно организованные устные упражнения учащихся в решении задач – важное средство активации мыслительной деятельности учащихся и развитии е их творческих способностей. Особое внимание заслуживают устные упражнения. Они эффективны кажущейся легкостью, эмоциональностью, действуют на учащихся мобилизующе, своей простотой увлекают и слабых школьников, создают в классе обстановку соревновательности. Устные упражнения способствуют развитию внимания и памяти учащихся, но они требуют от учащихся большого умственного напряжения, и поэтому сравнительно быстро утомляют их. Устный счет я всегда провожу так, чтобы ребята всегда начинали с легкого, а затем постепенно брались за вычисления все более и более сложных. Если сразу обрушить на учащихся сложные устные задания, то ребята обнаружат свое собственное бессилие, растеряются, и их инициатива будет подавлена.
Следует разделять два вида устного счета: первый – это тот, при котором учитель не только называет числа, с которыми надо оперировать, но и демонстрирует их учащимся каким-либо образом ( записывает на доске, указывает на таблице, проецирует на экран).Подкрепляя слуховые восприятия учащихся, зрительный ряд фактически делает ненужным удерживание данных чисел в уме, чем значительно облегчает процесс вычислений. Однако, именно запоминание чисел, над которыми производятся действия – важный момент устного счета. Тот, кто не помет удерживать числа в памяти в практической работе оказывается плохим вычислителем. Поэтому в школе нельзя недооценивать второй вид устного счета, когда числа воспринимаются только на слух. Учащиеся при этом не записывают и никакими наглядными пособиями не пользуются. Опишу кратко используемые мною формы устного счета.
В) Работы, подготавливающие учеников к изучению нового материала.
Изучение любого теоретического вопроса курса математики опирается на ранее пройденный материал, строится на известных учащимся фактах, правилах, выводах, которые являются частью новой информации. Это позволяет начать урок не с объяснения учителя, а с самостоятельной работы. Она не должна быть большой. В ходе ее выполнения учитель может внести дополнительные разъяснения. Упражнения составлены так, чтобы в процессе их выполнения школьники
-повторили определения, правила, математические факты, знание которых необходимо для понимания нового материала
-выполнили ранее изученные вычисления и преобразования, которые являются составной частью нового правила
=предугадали существование неизвестного для них алгоритма, формулы, понятия.
Таким образом, в процессе упражнений ученики уже изучают новый пункт программы. Во время проверки работы учитель делает обобщения, вводит новое понятие или правило. Это позволяет сократить время на объяснение. Приведем примеры.1) тема « Сравнение дробей с одинаковым знаменателем». Учитель раздает задание. А) начертите отрезок АВ. Отметьте 1/5 и 3/5отрезка АВ. Какая дробь больше-1/5 или 3/5? Запишите это с помощью знака .б) В первый день скосили сено с 3/10 участка, за два дня – с 7/10 участка. Какая из этих двух дробей меньше? Ответ запишите с помощью знака
Увеличьте 1,45 так, чтобы эта дробь стала целым числом. Во столько же раз увеличьте 3,335.
Разделите 333,5 на 145.
Работа дается в начале урока. Один из учеников выполняет упражнение на левой части доски. После проверки работы на правой части доски записывается пример деления на десятичную дробь 3,335:1,45. Таким образом, до объяснения нового материала на переносной доске получается запись. Объяснение нового материала проходит в виде фронтальной беседы. Учитель спрашивает, нельзя ли свести деление на десятичную дробь 1,45 к делению на целое число 145. Некоторые учащиеся догадываются, что надо перенести в делимом и делителе запятую на два знака, т.е. делимое и делитель умножить на 100. После этого выполнение деления 3,335:1,45 сводится к выполнению деления 333,5:1,45. Учитель еще раз разъясняет, почему истинно равенство 3,335: 1,45 = 333,5:145, и формулирует правило деления на десятичную дробь.
Г) Математические диктанты.
Важной задачей остаётся формирование у учащихся умения получать информацию на слух, запоминать, обрабатывать и преобразовывать эту информацию, а так же формирование грамотной и точной математической речи, правильное чтение числительных и математических выражений.
Помогают достичь этих целей математические диктанты. Математический диктант активизирует внимание школьников, позволяет быстро проверить и оценить их знания и умения, является хорошим организующим элементом урока.
В своей работе я пользуюсь "Математические диктанты 5-9 класс" (автор Е.Б.Арутюнян). Они помогают эффективно тренировать устойчивость внимания учащихся, оперативную память, умение сосредоточиться. Хочется отметить, что задания этих диктантов позволяют на только оценить знания и умения школьников, но и являются хорошим инструментом диагностики причин затруднения каждого ученика. Если математические диктанты проводятся регулярно, то они дисциплинируют учеников и обеспечивают систематический оперативный контроль за их работой.
Д) Устные контрольные работы
Важной задачей остаётся формирование у учащихся умения получать информацию на слух, запоминать, обрабатывать и преобразовывать эту информацию, а так же формирование грамотной и точной математической речи, правильное чтение числительных и математических выражений. Достичь этой цели могут устные упражнения контрольные работы.
Устные контрольные работы проводятся на заранее подготовленных карточках, мгновенно проверяются, носят как контролирующий характер, так и обучающий. В 5-6 классах могут иметь форму игры (морской бой), в старших классах- математический диктант. Мне более близка следующая методика проведения устной контрольной работы. На доске написан пример, ученики решают его устно. Через некоторое время учитель просит поднять руку тех, кто решил. Если с примером справилась большая часть класса, то ученики в тетрадях ставят номер примера и пишут ответ. В противном случае добавляется время для поиска ответа. Ответ записывается только по команде учителя. Если цель этой работы не только проверить знания, но и еще раз отработать какие-то вопросы теории, то разбор решения происходит сразу после того, как записан ответ. Тогда следующий пример составляется так, чтобы при его решении можно было использовать те приемы, с которыми они встретились при разборе. Устная контрольная работа несколько отличается от традиционной работы. Здесь ученик как бы сам себя контролирует при помощи заданий учителя. Сам он делает выводы об уровне усвоения, учитель не видит его неудач. Поэтому устная контрольная работа чаще имеет обучающий характер. Ученик поставлен в ситуацию, когда он вынужден работать в темпе, заданном учителем, контролировать свои действия и использовать весь материал темы. Сверхзадача урока – обучение рациональным приемам работы, без которых невозможно творчество. Работа может занимать как часть урока, так и весь урок. В этом учебном году я работаю в 9 и 10 классах, где чаще всего я провожу математические диктанты с самопроверкой и взаимопроверкой. Такие самостоятельные работы полезно проводить сразу после прохождения нового материала, в этом случае они своевременно дают картину понимания учащимися нового материала на самом раннем этапе его изучения. Самостоятельную работу даю в одном варианте. Работы 4-5 учеников, закончивших ее первыми, проверяются и оцениваются. Некоторые из этих учащихся сразу получают задания повышенной трудности. Я оказываю помощь тем детям, у которых возникли затруднения. Далее идет взаимная проверка - рядом с каждым заданием ставятся «+», «-», ученики сверяют ответы, в случае ошибки ищут ее, спорят, объясняют друг другу. На уроке постоянно чередуются индивидуальные и коллективные этапы работы. После того, как проверка закончена, на доске выписываются правильные ответы и решения трудных задач( если они есть), и ученики получают возможность еще раз сверить ответы, поспорить. Учитель узнает о количестве «+» и «-»в работе каждого ученика и может по своему усмотрению оценить некоторые из них. Задания повышенной трудности также можно оценить. В своей работе я пользуюсь "Математические диктанты 5 -9класс" (автор Е.Б.Арутюнян). Они помогают эффективно тренировать устойчивость внимания учащихся, оперативную память, умение сосредоточиться. Хочется отметить, что задания этих диктантов позволяют на только оценить знания и умения школьников, но и являются хорошим инструментом диагностики причин затруднения каждого ученика.
(Приложение 1).
Е) Самостоятельное приобретение знаний и умений (работа с книгой).
Самостоятельная работа учащихся, т. Е. их работа в отсутствие учителя или, по крайней мере, без обращения к его помощи в течение какого-то промежутка времени, является важнейшей частью всей работы по изучению математики. Многие вопросы школьного курса математики могут быть успешно изучены учащимися самостоятельно с помощью учебника, так как ученик имеет обучающую функцию, во многом аналогичную функции учителя. Но от учителя зависит сделать процесс приобретения знаний с помощью учебника более успешным – научить учащихся самостоятельно приобретать знания, научить их учиться.
Наиболее распространенными являются следующие виды работы с учебником
Чтение текста вслух
Чтение текста про себя
Воспроизведение содержания прочитанного вслух
Разбиение прочитанного текста на смысловые части - сначала это делает учитель, затем учащимся предлагается выполнить разделение текста на смысловые части и придумывание короткого заголовка из них - идет обучение составлению плана
Самостоятельно составление плана прочитанного
Работа с рисунками и иллюстрациями
Работа над понятием, термином
Самостоятельное составление плана прочитанного, который может быть использован учеником при подготовке к ответу
Работа с оглавлением и предметным указателем
Составление конспекта, схемы, таблицы, графика на основе материала, изученного по учебнику
Одним из способов организации работы учащихся с учебником математики является формирование приемов этой работы. На таких уроках удается добиться большей активности учащихся.
При работе с учебной литературой надо сообщить некоторые советы
Прочитайте заглавие. Знаете ли вы значение каждого слова? Если нет , то спросите у учителя. Выясните значения непонятных слов, встречающихся в тексте учебника.
Прочтите заглавие, подумайте, о чем пойдет речь в данном параграфе. Постарайтесь вспомнить, что вам уже об этом известно.
Если в тексте учебника есть задача, решите ее сами .Можете ли вы придумать аналогичную задачу? Что разъясняют приведенные автором учебника задача или примеры? Какие примеры или задачи с той же целью приводил учитель на уроке?
С какими новыми определениями вы встретились при чтении этого параграфа? Повторите их про себя. Приведите свои примеры, разъясняющие определения.
Ж) Обучающие самостоятельные работы.
Самостоятельные работы обучающего характера практикую для закрепления математических знаний, для развития способности к практическому применению этих знаний, а также для овладения необходимыми навыками. Как правило, почти на каждом уроке математики некоторая часть учебного времени отводится исключительно для самостоятельного выполнения учащимися каких-либо тренировочных заданий. Такие задания обычно составляю из упражнений или из задач стандартного типа (т. е. заданий, выполняемых по данному ученику образцу) или представляют собой самостоятельное воспроизведение известных учащимся выводов формул, доказательств теорем, составления таблиц и т. п. Во время выполнения такой самостоятельной работы я подхожу к каждому ученику, оказываю им индивидуальную помощь при необходимости ( постановкой наводящего вопроса, требованием сделать проверку, указанием на допущенную ошибку и т. п.). Тренировочные задания для самостоятельной работы должны быть доступными для выполнения «среднему» ученику, их располагаю в порядке возрастания трудностей, они должны содержать 1-2 задачи для более «сильных» учащихся. Наиболее часто применяемым видом самостоятельной работы являются задания, аналогичные тому, которое выполнялось с помощью учителя. Так, например, если вместе с учениками коллективно выведены формулы приведения для углов на промежутке 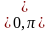 и выявлен общий метод получения этих формул, то вывод формул приведения для углов в промежутках
и выявлен общий метод получения этих формул, то вывод формул приведения для углов в промежутках 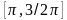 ,
, 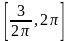 , будет полезным самостоятельным упражнением тренировочного характера. Следует учитывать, что задания должны быть разнообразными, иначе ученики будут выполнять их механически, без всякого желания и интереса. Так же полезным самостоятельным упражнением может явиться, например, вывод формулы решения приведенного квадратного уравнения, после того как вывод формулы для решения общего квадратного уравнения будет изучен совместно с классом. После выполнения учащимися этого задания следует подчеркнуть, что при проведении того или иного математического вывода или доказательства очень часто применяется сведение неизвестного случая к известному, путем соответствующих преобразований. Если изучаем трудный для учащихся вопрос, то после его изучения предлагаю ребятам сначала поработать с учебником, затем разобрать совместно решение нескольких ключевых задач и только потом предлагаю учащимся упражнения для самостоятельной работы. На практике также применяю такое виды самостоятельных работ, как решение задач с последующей проверкой (ученики выполняют задание самостоятельно, затем проверяют свою работу по показанному образцу, при этом учитель поэтапно выясняет осмысленность решения путем постановки соответствующих вопросов), многовариантные задания с готовыми ответами (эти работы помогают быстрому установлению обратной связи, выявлению пробелов и разбору неясных ситуаций), самостоятельная работа с показом( такая работа позволяет учащимся не только увидеть, как надо решать задачу, но и самостоятельно установить логические связи между увиденным и тем, что надо сделать), работа по заданному алгоритм у ( она приучает учеников к четкому, последовательному выполнению задания, целенаправленно организует мыслительную деятельность учащихся). (Приложение 2).
, будет полезным самостоятельным упражнением тренировочного характера. Следует учитывать, что задания должны быть разнообразными, иначе ученики будут выполнять их механически, без всякого желания и интереса. Так же полезным самостоятельным упражнением может явиться, например, вывод формулы решения приведенного квадратного уравнения, после того как вывод формулы для решения общего квадратного уравнения будет изучен совместно с классом. После выполнения учащимися этого задания следует подчеркнуть, что при проведении того или иного математического вывода или доказательства очень часто применяется сведение неизвестного случая к известному, путем соответствующих преобразований. Если изучаем трудный для учащихся вопрос, то после его изучения предлагаю ребятам сначала поработать с учебником, затем разобрать совместно решение нескольких ключевых задач и только потом предлагаю учащимся упражнения для самостоятельной работы. На практике также применяю такое виды самостоятельных работ, как решение задач с последующей проверкой (ученики выполняют задание самостоятельно, затем проверяют свою работу по показанному образцу, при этом учитель поэтапно выясняет осмысленность решения путем постановки соответствующих вопросов), многовариантные задания с готовыми ответами (эти работы помогают быстрому установлению обратной связи, выявлению пробелов и разбору неясных ситуаций), самостоятельная работа с показом( такая работа позволяет учащимся не только увидеть, как надо решать задачу, но и самостоятельно установить логические связи между увиденным и тем, что надо сделать), работа по заданному алгоритм у ( она приучает учеников к четкому, последовательному выполнению задания, целенаправленно организует мыслительную деятельность учащихся). (Приложение 2).
Во время выполнения обучающей работы учащимся, которые сидят за одной партой, разрешается консультироваться друг с другом. Один из них может помочь другому разобраться в объяснительном тексте или решении одного – двух примеров. Но даже в этом случае каждый ученик выполняет основное задание самостоятельно. Это гарантируется различными вариантами работы. За обучающую работу ученикам выставляется только положительная оценка. По своему усмотрению учитель может внести в работу изменения, например
Сократить или увеличить число упражнений
Изменить последовательность упражнений
Предложить учащимся выполнить всю работу или ее часть дома.
Однако все изменения не должны нарушать логическую последовательность системы упражнений и принципов дидактики.
З) Контролирующие самостоятельные работы.
Важным и чрезвычайно тонким моментом учебного процесса как для учителя, так и для ученика является контроль за знаниями учащихся. После того, как материал хорошо усвоен и учащиеся без особых затруднений справляются с самостоятельными работами обучающего характера, необходимо проверить и оценить приобретенные ими знания. Контролирующие работы целесообразно проводить после логически завершенных циклов учебного материала, что дает возможности проверить степень усвоения материала в каждом из этих циклов. Поскольку проверочные работы проводятся после отработки основных умений и навыков, то нет необходимости включать в эти работы задания только репродуктивного характера. В тоже время в таких работах не следует включать задания сложнее тех, которые выполнялись на уроках и дома. Порядок расположения заданий в проверочных работах не играет такой роли, как в обучающих, так как проверяемые знания и навыки отработаны. (Приложение3)
И) Зачеты.
Система тематических зачётов позволяет проверку обязательных результатов обучения сочетать с проверкой на более высоком уровне, а условия её проведения дают возможность объективнее и точнее дифференцировать учащихся по уровню их подготовки.
К)Таблицы.
При проведении самостоятельных работ одним из наиболее наглядных пособий, применяемых на уроках математики, является таблицы. По своему основному назначению таблицы могут быть подразделены на справочные, иллюстрированные и рабочие, называемые также таблицами-заданиями.
Таблицы-задания, используемые на уроках алгебры наряду с дидактическими раздаточными материалами, а иногда и совместно с ними, позволяют организовать самостоятельную работу учащихся, сочетать фронтальную и индивидуальные формы работы при закреплении пройденного, организовать повторение и систематизировать изучение материала.
Удобно использовать таблицы-задания и при опросе учащихся у доски, а в ряде случаев при опросе и фронтальной проверке выполненных учащимися самостоятельных заданий.
В отдельных случаях при проведении самостоятельной работы с целью проверки усвоенного теоретического материала могут быть использованы и иллюстрированы таблицами.
Работа с использованием таблиц-заданий может строиться в форме устных упражнений проведённых фронтально, диктантов, самостоятельных письменных работ. Кроме того, по таблицам можно осуществлять и фронтальную проверку выполненной самостоятельной работы, в том числе с вызовом отдельных учащихся к доске.
Таблица «Область определения выражения»
|
| А | В | С | Д |
| 1 |
|
|
|
|
| 2
|
|
|
|
|
| 3
|
|
|
|
|
| 4
|
|
|
Lq(36-X2) |
Lq(lqX) |
| 5 |
|
|
|
|
C помощью этой таблицы можно организовать как фронтальную работу на уроке, так и опрос учащихся у доски и самостоятельную письменную работу. При ответе на поставленный вопрос учащиеся должны давать развернутый обоснованный ответ. Например, находя область определения выражения 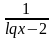 , ученик может рассуждать так « Для существования lqx необходимо и достаточно, чтобы переменная х принимала положительные значения, т. е. выполнялось неравенство х0.Чтобы имела смысл дробь, необходимо, чтобы ее знаменатель не был равен нулю, т. е. чтобы выполнялось неравенство lqx-2≠0 . Отсюда lqx≠2,x≠100.Следовательно,х-любое положительное число, не равное 100.С использованием таблицы можно провести самостоятельную работу, рассчитанную на 5-7 минут
, ученик может рассуждать так « Для существования lqx необходимо и достаточно, чтобы переменная х принимала положительные значения, т. е. выполнялось неравенство х0.Чтобы имела смысл дробь, необходимо, чтобы ее знаменатель не был равен нулю, т. е. чтобы выполнялось неравенство lqx-2≠0 . Отсюда lqx≠2,x≠100.Следовательно,х-любое положительное число, не равное 100.С использованием таблицы можно провести самостоятельную работу, рассчитанную на 5-7 минут
1 вариант 2 вариант
Найти область определения выражения
С4,2) Д2 1) С3,2) Д1
При каких значениях переменной равно нулю значение выражения
А2 А3?
Л) Учебный проект.
Главным смыслом исследования в образовании есть то, что оно является учебным. Это означает, что его главной целью является развитие личности, а не получение объективно нового результата, как в “большой” науке. Если в науке главной целью является производство новых знаний, то в образовании цель исследовательской деятельности – в приобретении учащимися функционального навыка исследования, развитии способности к исследовательскому типу мышления, активизации личностной позиции ученика в образовательном процессе. И главное, самостоятельно получаемых знаний, которые являются новыми и значимыми для конкретного ученика.
М) Тесты.
Перед педагогами школ поставлена задача подготовки детей к тестированию. Тестирование является одним из важных элементов итоговой и промежуточной аттестации учащихся. Этот метод диагностики, по мнению многих авторов, является одним из наиболее достоверных и объективных.(Приложение 5).
Типы и виды тестовых заданий представлены в таблице. 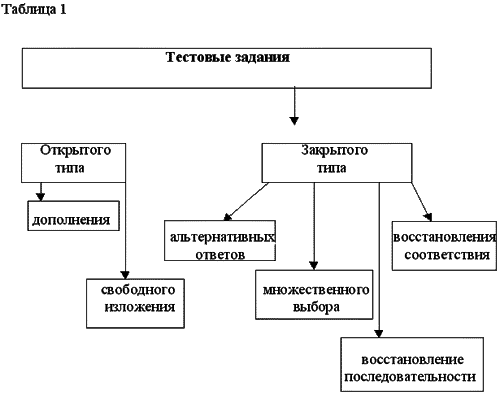
6. Цели, задачи и функции самостоятельной работы учащихся
Весь процесс обучения направлен на достижение определенной цели - формирование и воспитание многогранной, творческой личности, с сложившимися приоритетами, правилами поведения, с системой ценностей и верными представлениями о мире в целом. Поэтому любая деятельность учителя должна носить целенаправленный характер. Очевидно, что педагог лишь организует и направляет познавательную деятельность обучаемых. Ее эффективность зависит от собственных усилий последних. При правильной организации самоподготовка имеет решающее значение для развития самостоятельности как одной из ведущих черт ученика и выступает средством, обеспечивающим для школьников:
-сознательное и прочное усвоение знаний по предмету;
-овладение способами и приемами самообразования;
-развитие потребности в самостоятельном пополнении знаний.
Самоподготовка способствует формированию высокой культуры умственного труда, приобретению приемов и навыков самостоятельной работы, умений разумно расходовать и распределять свое время, накапливать и усваивать необходимую для успешного обучения и профессионального становления информацию. Она развивает у учеников такие качества, как организованность, дисциплинированность, инициативность, волю; вырабатывает мыслительные умения и операции (анализ, синтез, сравнение, сопоставление и др.), учит самостоятельному мышлению, позволяет сформировать свой собственный стиль работы, наиболее полно соответствующий личным склонностям и познавательным навыкам школьника. В условиях же высокого уровня развития науки и техники особые требования предъявляются именно к подготовке учащихся в школе. Задача образования не может сводиться только к вооружению учащихся определенной суммой знаний. Необходимо сформировать у них умение оперировать приобретенными знаниями, применять их в новых ситуациях, делать самостоятельные выводы и обобщения, находить решения в нестандартных условиях. В настоящий период когда развитие науки и техники происходит чрезвычайно быстро, когда делаются всё новые и новые научные открытия, когда появляются неизвестные ранее отрасли науки, техники, экономики, исключительную значимость приобретает проблема подготовки учащихся к самостоятельному овладению новыми знаниями, к изучению научной и технической литературы. Для этого им необходимы такие умения как читать текст, насыщенный информацией, вычленять из него главное, ставить перед собой вопросы и находить в тексте ответы на них, определять, что осталось не выясненным до конца, четко формулировать, что именно надо выяснить, обращаться за справкой к другому разделу книги или другой литературе и т.п. Вместе с тем, для того чтобы подготовить учащихся к применению знаний в конкретных условиях, к решению сложных вопросов, выбору из имеющегося набора решений оптимального варианта и т.д., необходимо сформировать определенные умения в решении задач. Самостоятельная деятельность учащихся можно и нужно организовывать на различных уровнях, от воспроизведения действий по образцу и узнавание объектов путем их сравнения с известным образцом до составления модели и алгоритма действий в нестандартных ситуациях.
Это переориентирует самостоятельную работу с традиционной цели - простого усвоения знаний, приобретения умений и навыков, опыта творческой и научно-информационной деятельности - на развитие внутренней и внешней самоорганизации учащегося, активно преобразующего отношения к получаемой информации, способности выстраивать индивидуальную траекторию самообучения.
Данная особенность постановки целей имеет дидактическое значение для педагогической деятельности - преподаватель может ориентироваться на представленную номенклатуру при организации и самостоятельной работы учащихся. Вместе с тем важно научить школьника самого ставить перед собой цели. На разных занятиях в ходе анализа нового материала, при проверке заданий желательно вначале подводить учащегося к пониманию цели педагога, а затем к самостоятельной постановке своих, имеющих для него личностный смысл целей. Важное условие при этом - цели школьников должны быть реально достижимыми.
Общей же целью самостоятельной работы учеников при изучении математики является формирование математического мышления учеников.
Эта цель самостоятельной работы при изучении математики конкретизируется в задачах самостоятельной работы по каждой теме, среди которых выделяются приоритетные.
Для достижения поставленных целей большое значение имеют условия организации самостоятельной работы, которые позволяют значительно повысить ее эффективность. К ним можно отнести индивидуализацию, которая включает:
увеличение удельного веса интенсивной работы с более подготовленными учащимися;
деление занятия на обязательную и творческую части (для всех, пытающихся самостоятельно справиться с более трудными и, главное, - нестандартными задачами, дополнительными вопросами, учебно-проблемными ситуациями и т. д.);
регулярность консультаций с обучаемыми;
исчерпывающее и своевременное информирование о тематическом содержании самостоятельной работе, сроках выполнения, потребности во вспомогательных средствах, формах, способах контроля и оценке итоговых результатов с обязательным сравнением с ожидаемыми.
Данные условия определяют применение личностно-ориентированного подхода при обучении, который способствуют полноценному раскрытию способностей каждого из обучающихся и последующему творческому развитию.
При постановке целей и задач самостоятельной работы необходимо учитывать следующие дидактические требования:
1. Самостоятельная работа должна носить целенаправленный характер.
2. Самостоятельная работа должна быть действительно самостоятельной и побуждать ученика при ее выполнении работать напряженно.
3. На первых порах у учащихся нужно сформировать простейшие навыки самостоятельной работы.
4. Для самостоятельной работы в большинстве случаев нужно предлагать такие задания, выполнение которых не допускает действия по готовым рецептам и шаблону. 5. В организации самостоятельной работы необходимо учитывать, что для овладения знаниями, умениям и навыками различным учащимися требуется разное время.
6. Задания, предлагаемые для самостоятельной работы, должны вызывать интерес учащихся.
7. Самостоятельные работы учащихся необходимо планомерно и систематически включать в учебный процесс.
8. При организации самостоятельной работы необходимо осуществлять разумное сочетание и изложения материала учителем с самостоятельной работой учащихся по приобретению знаний, умений и навыков.
9. При выполнении учащимися самостоятельных работ любого вида руководящая роль должна принадлежать учителю.
Самостоятельная работа обладает большим потенциалом для развития различных умений школьников. Организация самостоятельной работы, руководство ею - это ответственная и сложная работа каждого учителя. Воспитание активности и самостоятельности необходимо рассматривать как составную часть воспитания учащихся. Эта задача выступает перед каждым учителем в числе задач первостепенной важности
Результативность .
Работа над проблемой формирования навыков самостоятельной учебно – познавательной деятельности учащихся при изучении математики в школе дает свои положительные результаты: за 3года обучения повышается не только уровень мотивации к предмету математика, но и в тоже время растет качество знаний и уровень обученности.
Ежегодно мною как учителем и как классным руководителем , из класса в класс, отслеживается уровень мотивации учащихся по предметам(используются методики: Социометрия,
Методика «Наши отношения», Методики А.А. Андреева и Е.Н. Степанова).
Результаты диагностики по выявлению уровня мотивации по математике в 7-9 классах были обработаны мною за последние три учебных года (с 2006 г по 2009г) и представлены на графике.
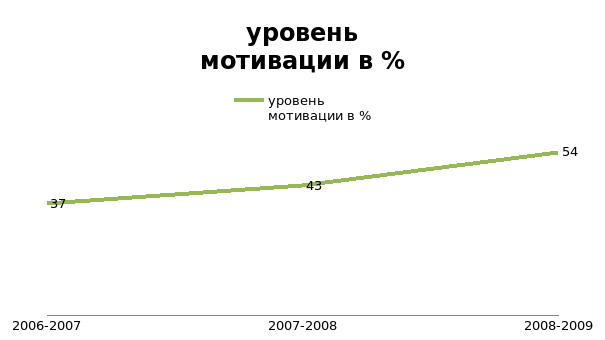
Из графика видно, что уровень мотивации к обучению учащихся
по математике растет с 37% до 54% и ежегодно возрастает на 6-11%.
Наряду с уровнем мотивации обучения учащихся по предмету
отслеживалась их позитивная динамика общей успеваемости и качества
знаний по математике. В период с 2007-2008 учебного года по 2009-2010
учебный год качество знаний учащихся по математике при
100% успеваемости представлено на диаграммах.
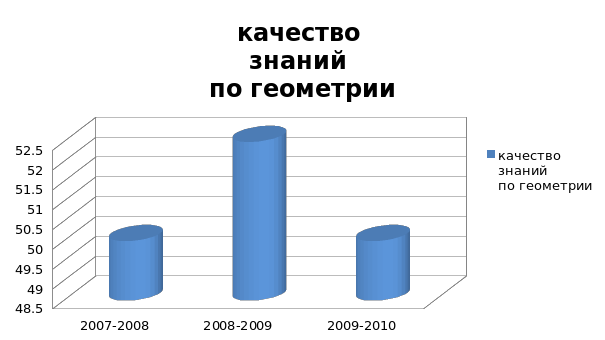
Большое положительное влияние на развитие интереса к математике в
процессе обучения оказывает применение элементов игровой технологии
не только на уроках, но и во внеурочное время. Этим объясняется ежегодный
рост численности учащихся 5-11 классов, желающих принять участие в международной математической игре «Кенгуру».
Среди учащихся выделяется группа особо интересующихся математикой- учащиеся с интересом посещают внеклассные занятия, работают над интересующими их научными темами, решают задания повышенной сложности, работают с научной литературой ,используют учебные порталы и сайты Интернет, с интересом работают с офисными программами. Основной целью занятий с такими ребятами является проведение научно – исследовательской работы. Ребятами рассмотрены вопросы «Функции и графики», «Пушкин и математика», «Графы Эйлера», «Исследование золотого сечения» и другие.
Работы учащихся творческой группы вызывают особый интерес, и привлекают к себе внимание сверстников.
Показателем опыта работы по проблеме «Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе» является участие школьников в районных и школьных олимпиадах по математике. По результатам 2009/2010г.г. ученица 9 класса Красавина Анна заняла 1 место.
Участвую в работе городского методического объединения учителей
математики, делюсь своим опытом работы. Мною были подготовлены доклады: «Новая форма итоговой аттестации по математике для учащихся 9 классов – особенности структуры, организации ее проведения, оценивания»,
темы моих выступлений на школьном заседании кафедры учителей математики, физики и информатики «Развитие творческих способностей учащихся на уроках математике», «Уроки математики в рамках концепции личностно-ориентированного обучения».
Считаю необходимостью продолжить работу по теме «Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе», так как работа над самообразованием и совершенствованием приемов и методов работы открывает новые горизонты для развития интереса и творческой активности школьников.
Заключение
Изменения, происходящее в мире заставляют общество предъявлять новые требования к современному человеку. Начинает уделяться внимание его умению адаптироваться к быстро изменяющимся условиям. При этом он должен на протяжении всей своей жизни заниматься самообразованием, для того чтобы быть хоть в некоторой степени успешным. Поэтому одной из главных задач среднего образования является формирование у учащихся умения оперировать приобретенными знаниями, применять их в новых ситуациях, делать самостоятельные выводы и обобщения, находить решения в нестандартных условиях. Также, что основополагающим требованием общества к современной школе является формирование личности, которая умела бы самостоятельно творчески решать научные, производственные, общественные задачи, критически мыслить, вырабатывать и защищать свою точку зрения, свои убеждения, систематически и непрерывно пополнять и обновлять свои знания путем самообразования, совершенствовать умения, творчески применять их в действительности. Эффективное использование самостоятельной работы позволяет решать большой ряд вышеперечисленных задач.
При этом самостоятельная работа учащихся при изучении математики в школе является важной составляющей учебно-воспитательного процесса. Ее целесообразно рассматривать как форму организации учебной деятельности учащихся, осуществляемую под прямым или косвенным руководством преподавателя, в ходе которой учащиеся преимущественно или полностью самостоятельно выполняют различного вида задания с целью развития знаний, умений, навыков и личных качеств.
Анализ теоретических исследований проблемы применения самостоятельной работы в школе позволил определить ее цели, задачи, функции, технологию организации, классификацию.
При этом самостоятельная работа обучающегося, в общем контексте его самообразования, является высшей формой его учебной деятельности по критерию саморегуляции и целеполагания; она может дифференцироваться в зависимости от источника управления, характера побуждений и др.
Очевидно, что возможности применения самостоятельной работы как
формы организации учебного процесса в школе достаточно широки. При этом самостоятельные работы можно классифицировать на обучающие, тренировочные, закрепляющие, повторительные, развивающие, творческие, контрольные. Хотя это не единственное основание для классификации данной формы деятельности, и каждый из перечисленных выше видов не встречается в школьной практике отдельно.
Любая организованная учителем самостоятельная работа школьника должна отвечать следующим дидактическим требованиям: иметь целенаправленный характер; быть действительно самостоятельной работой и побуждать ученика при ее выполнении работать напряженно; при этом на первых порах у учащихся нужно сформировать простейшие навыки самостоятельной работы; для самостоятельной работы в большинстве случаев нужно предлагать такие задания, выполнение которых не допускает действия по готовым рецептам и шаблону; задания должны вызывать интерес у учащихся; самостоятельную работу необходимо планомерно и систематически включать в учебный процесс; при организации самостоятельной работы необходимо осуществлять разумное сочетание изложения материала учителем с самостоятельной работой учащихся по приобретению знаний, умений и навыков; при выполнении учащимися самостоятельных работ любого вида руководящая роль должна принадлежать учителю.
Литература.
1. Самостоятельная деятельность учащихся при обучении математике (формирование умений самостоятельной работы): Сб. статей / Сост. С.И. Демидова. Л.О. Денищева. - М.: Просвещение, 1985.
2. Буряк, В. К. Самостоятельная работа учащихся / В.К. Буряк. - М.: Просвещение, 1984.
3. Зимняя, И. А. Педагогическая психология: Учебник для вузов. Изд. Второе, доп., испр. и перераб / И.А. Зимняя - М.: Лотос, 2001.
4. Педагогика / Под ред. Ю.К. Бабанского. - 2-е изд., доп. и перераб. - М.: Просвещение, 1988.
5. Пидкасистый П. И. Самостоятельная познавательная деятельность школьников в обучении: Теоретико-экспериментальное исследование / П.И. Пидкасистый. - М.: Педагогика, 1980.
6. Эльконин, Д.Б. Избранные психологические труды: Проблемы возрастной и педагогической психологии / Под ред. Д.И. Фельдштейна. - М.: Междунар. пед. академия, 1995.
7. Занков Л.В. Развитие школьников в процессе обучения.
8. Кордемский Б.А. Увлечь школьников математикой.– М.:Просвещение,1981.
9. Окунев А.А. Спасибо за урок, дети! О развитии творческих способностей учащихся.
Книга для учителей: Из опыта работы.– М.:Просвещение,1988.
10. Щукина Г.И. Проблема познавательного интереса в педагогике.– М.:Педагогика,1971.
Статьи из журнала «Математика в школе»
1. Акири И.К. Интеллектуальные игры на уроках математики.2000, №5, с.8.
2. Аут К.Х., Виленкин Н.Я. О роли основных принципов дидактики в преподавании
школьного курса математики.1987, №1, с.41.
3. Ахметгалив А. Мотивация деятельности на уроках математики1996, №2, с.59.
4. Барчунова Ф. Развитие познавательного интереса к геометрии учащихся VI–VII классов. 1974, №6, с.25.
5. Баранова Е.В., Зайкин М.И. Как увлечь школьников исследовательской деятельно-
стью. 2004, № 2, с.7.
Приложения.
Приложение 1.
6 класс.
Тема «Степень»
Запишите степень с основанием 3(6) и показателем 2( 4).
Запишите в виде степени произведение, состоящее из четырех(пяти0 множителей, каждый из которых равен А (В).
Запишите выражение 105 (104).
Найдите значение четвертой (третьей) степени числа -2 (-3).
Найдите значение пятой(восьмой) степени числа -1(0).
Найдите значение шестой(восьмой) степени числа 1(-1).
Запишите в виде произведения степень с основанием Х(У) и показателем 3(4).
Найдите значение седьмой степени числа 0(1).
7 класс.
Тема «Линейное уравнение с одним неизвестным»
Придумайте и запишите какое-либо линейное уравнение с одним неизвестным Х (У).
Как называется уравнение -2Х=17? (17х= -2)?
При каком условии уравнение СХ=5 (АУ=3) имеет единственный корень? ( не имеет корней?). запишите этот корень.
Решите уравнение 0,2Х=-1. ( -0,3 У =1).
К обеим частям уравнения прибавили число -3.(Обе части уравнения умножили на число -7).Какими являются полученное и исходное уравнения?
Решите уравнение 2Х+1= 3Х-Х. (Х+3=5+Х-2).
Решите уравнение 5-Х=2Х+2. (2-2Х=-2Х+3).
8 класс.
Тема «Степень с натуральным показателем»
Запишите в виде произведения третью (четвертую) степень числа 4 (3) и найдите ее числовое значение.
Чему равна первая степень числа -5? (2/3)
Вычислите значение выражения 23*24 (32*33)
Чему равна сумма кубов (квадрат разности) чисел 5 и 3 (3 и 2)?
Вычислите квадрат куба числа 3 (куб квадрата числа 2).
9 класс.
Тема «Степень с целым показателем»
Дайте определение нулевой степени числа Х (У).
Запишите выражения 52,70,2-3, ( 3-2, 24, 60) и найдите их значения.
Представьте дробь 1/35 ( 1/33) в виде степени с отрицательным показателем.
Запишите выражение Х-3*Х7 (А6*А-10) . Представьте его в виде степени.
Запишите степень, которая получится, если выражение Х-5 (У-7) возвести в минус четвертую степень?
Для каких Х,У и А (К,Р и В) верно, что Ах/Ау =АХ-У 9 В К-Р= ВК/ВР) ?
Приложение 2.
Обучающая самостоятельная работа по теме «Вычитание положительных и отрицательных чисел»
Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел : по данной сумме и одному из слагаемых находят другое слагаемое.
Рассмотрим уравнение Х+8=17. Искомое слагаемое находится вычитанием: Х=17 – 8. Вы знаете, что 17 – 8=9. Значение разности 17 – 8 можно найти по другому: к уменьшаемому прибавить число, противоположное вычитаемому: 17+( -8)=9. Итак, 17 – 8 =17 + (-8).
Вообще, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
П Р И М Е Р Ы
А) 18 – (-9)=18 + 9 = 27
Б)25 – 40 =25 +(-40)= -15
В) -25 – (-40) = -25+40=15
Г)-40 – 25 = -40 + (-25)= -65.
УПРАЖНЕНИЯ.
Найдите пример, в котором неверно выполнена замена вычитания сложением. Решите его, объяснив ошибку
А) 2 – 10= 2 + (-10)
Б) -4-3= -4+(-3)
В) -4-3= -4+3
Г) -15-(-21)=-15+21.
2. Не выполняя действия, замените вычитание сложением
А) 48-52 в) 0,6- (-2,8)
Б) 17,5-(-25) г) -573-0,4.
3. Выполните действия
А) 6-13 д) 13-6
Б) 6-(-13) е) 13-(-6)
В) -6-(-13) ж) -13-6
Г) -6-13 з) -13-(-6).
4. Вставьте пропущенное слово
Чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число,…..вычитаемому.
5. Вместо звездочки запишите переменную, чтобы получилось верное равенство для любых значений а и в а - в = а + *.
6. Проверьте, правильно ли найдена разность
А) 0,789-(-1392)=1392,789
Б) 0,5-(-160)=-159,5.
Объясните ошибку в неверно решенном примере.
7. Заполните таблицу
| А | 10 | -10 | 10 | -10 |
| Б | 27 | -27 | -27 | 27 |
| А-Б |
|
|
|
|
8. Найдите значение выражения а - с, если
А) а=0 с=238
Б) а=0 с=-1,58
В) а=-1,58 с=0.
9. Выполните вычитание -30-(-8).
Какие из примеров а) -30+8 б) -30-8 в) 8-30 -имеют тот же ответ? Объясните почему.
10. Какие равенства и неравенства верны
А) -3-17
б) 10-(-101)101+10 г)-5-(-11)=-5-11?
11. Решите уравнение
А) -6,5+Х=4,5
Б) Х+11=-12,5.
12.Вместо звездочки поставьте знак =, ,чтобы получилось верное равенство или неравенство
А) 5-(-10)*15
Б) -5-(-5)*-15
В) -10-(-5)*-15.
Обучающая самостоятельная работа по теме «Сложение чисел с разными знаками»
Задача. Температура воздуха в полдень была -10 градусов, к вечеру изменилась на 2 градуса. Какая температура стала вечером?
Решение. Задачу будем решать сложением. Температура изменилась на 2 градуса, т. е. повысилась на 2 градуса и стала -8 градусов, следовательно, -10+2=-8.
Сумма двух чисел с разными знаками есть число, которое имеет тот же знак, что и слагаемое с большим модулем. Чтобы найти модуль суммы, надо из большего модуля вычесть меньший.
Пример. Найдем сумму -9+6.
1-й шаг. Найдем знак суммы. Для этого сравним модули слагаемых. Модуль числа -9 больше модуля числа 6, поэтому сумма отрицательна.
2-й шаг. Найдем модуль суммы. Он равен разности модулей слагаемых, т. е. 9-6=3.
3-й шаг. Найдем сумму -9+6=-3.
У П Р А Ж Н Е Н И Я.
Не производя сложения, укажите примеры, в которых сумма отрицательна
А) -4,25+679 в) -792,8+793
Б) 2,5+(-600) г) 279+(-280,9).
2. Выполните сложение
А)-7+50 г) -48+8 ж) 0,1+(-4,9)
Б) 7+(-50) д) 1+(-29) з) 0,06+(-0,6)
В) 48+(-8) е) -3,8+6,1
3. На математических состязаниях капитанам команд были предложены два вопроса. Если ответ на первый вопрос был верный, то капитан получил 2 очка, если неверный-2 очка. Если ответ на второй вопрос был верный, капитан получал 4 очка, если ответ неверный-4 очка.
Капитан ответил верно на оба вопроса. Сколько очков он получил за этот вид соревнования?
Найдем сумму чисел 2 и 4 2+4=6.
Капитан получил 6 очков. Будем считать, что ответ на вопрос « Сколько очков капитан получил за этот вид соревнования?»- находится сложение независимо от того, будут ли данные числа положительны или отрицательны.
Ответьте на следующие вопросы
Сколько очков получил капитан за этот вид соревнований а) если он ответил неверно на оба вопроса
Б) если он ответил верно на первый вопрос и неверно на второй
В) если он ответил неверно на первый вопрос и верно на второй?
4. Найдите значение переменной Х, при котором верно равенство
А) 3,5+7=Х в) 0,2+(-7,2)=Х
Б) -4,8+(-5,2)=Х г)-8,1+(-4,1)=Х.
5. Найдите значение выражения
А) а + в, если а=-11,в=-29
Б)с + д , если с=-1,8, д=7
В) х + в, если х=0, в=-1
Г) м + н, если м=-800, н=0.
6. Заполните таблицу
| А | -5 | 3000 | -71 | -900 |
| Б | 15 | -100 | -79 | 10 |
| А+Б |
|
|
|
|
| Б+А |
|
|
|
|
7. Найдите значение выражения
А) 41,9+(-26,8)+(-15,1) б) -76,8+(-46,8)+(-26,8).
8. Вместо звездочки поставьте знак =, , чтобы получилось верное равенство или неравенство
а) -3,8+1,7 *-2,1 в) 3,8 +(-1,7) * -2,1
б) -3,8-1,7 *-5,6г) -3,8+1,7 *+5,6.
Приложение 3.
Тема: логарифмические уравнения.
Решите уравнение
|
3) lg (x–1) + lg (x+1)=0
|
|
Вычислите:
| 1) 2)
|
|
Тема: тригонометрические уравнения
| Карточка 1
| Карточка 3
|
| Карточка 2
| Карточка 4
|

 Получите свидетельство
Получите свидетельство Вход
Вход



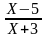
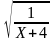
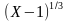
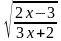
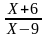
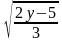
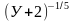
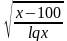
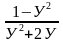
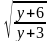
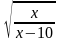
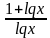
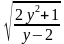
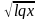
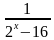
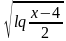









 Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе (159 KB)
Формирование навыков самостоятельной учебно-познавательной деятельности учащихся при изучении математики в школе (159 KB)
 0
0 568
568 40
40 Нравится
0
Нравится
0


