Fdafdasf adf sadfdsfsd

Исследовательский проект

Решение задач с помощью графов

Подготовил:

Ученик 7 «б» класса

Болотов Максим

г. Коряжма

2019 г.

Оглавление

Аннотация 3

Введение 4

Теория графов 5

Виды графов 6

Примеры решения задач 8

Заключение 16

Цель данной работы – изучение теории графов, применение графов для решения задач, в том числе задач олимпиадного уровня.

Задачи:

1. Изучить теорию графов;

2. Рассмотреть способы решения задач;

Методы, используемые в данном исследовании:

1. Изучение и обобщение

2. Анализ и синтез

Меня удивило, как легко и просто решаются с помощью графов задачи, которые не сразу понятны после прочтения. Поэтому мне более подробно захотелось разобраться в этой теме.

Математика - это очень непростая наука, можно сказать, что очень сложная. И сейчас мы рассмотрим несложную тему в математике, которая называется - ТЕОРИЯ ГРАФОВ В РЕШЕНИИ ЗАДАЧ.

Теория графов один из наиболее интересных разделов математики. Родоначальником теории графов считается швейцарский математик Леонард Эйлер, который в 1736 году сформулировал решение задачи о семи кёнигсбергских мостах, ставшей впоследствии классической задачей теории графов. Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.

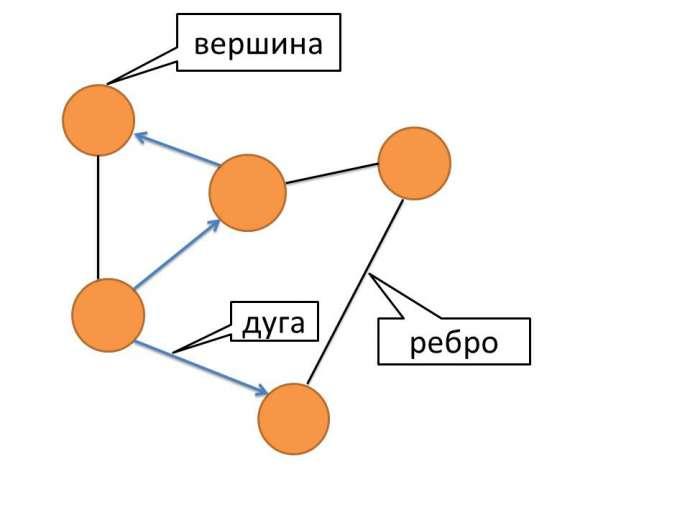
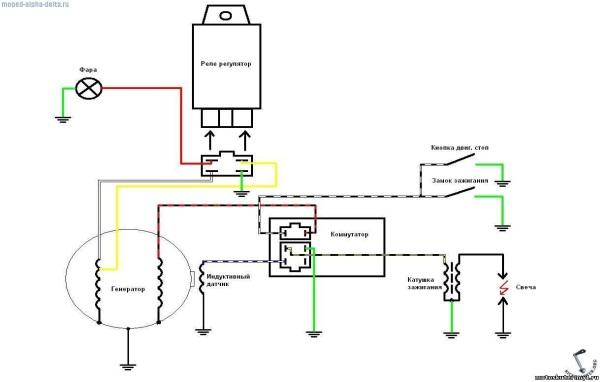
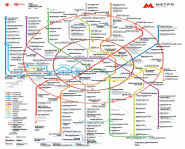
Примеры графов: схемы авиалиний, метро, дороги, электросхемы, чертежи многоугольников.

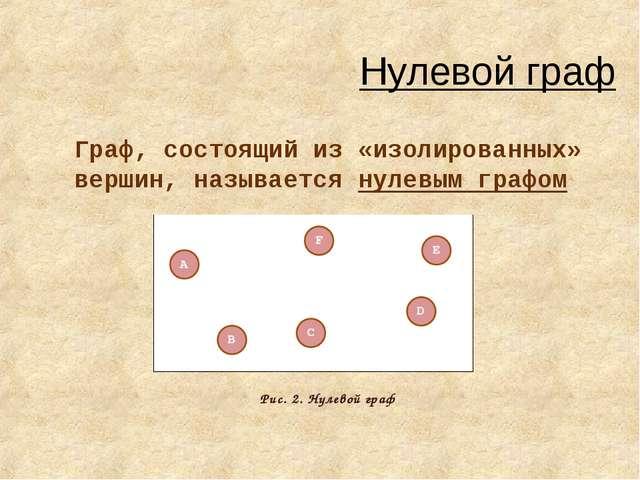
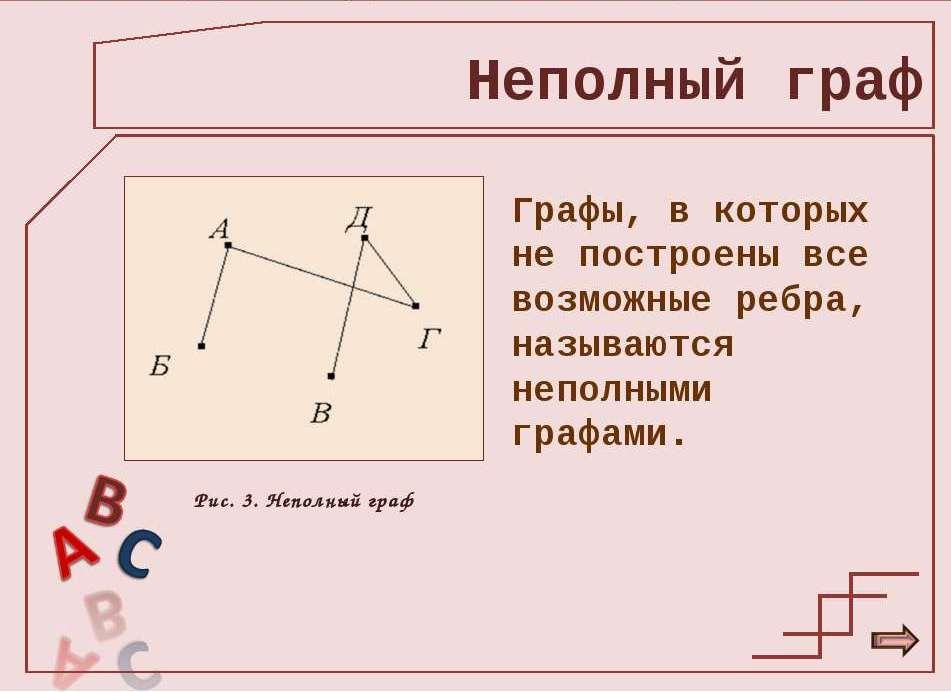
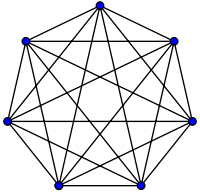
Графы, в которых построены все возможные ребра, называются полными графами.

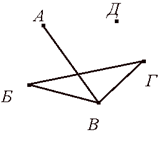
Количество рёбер, выходящих из вершины графа, называется степенью вершины.

Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.

Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.

На рисунке изображен граф с пятью вершинами. Степень вершины А обозначим Ст. А. На рисунке: Ст. А = 1, Ст. Б = 2, Ст. В = 3, Ст. Г= 2, Ст. Д= 0.

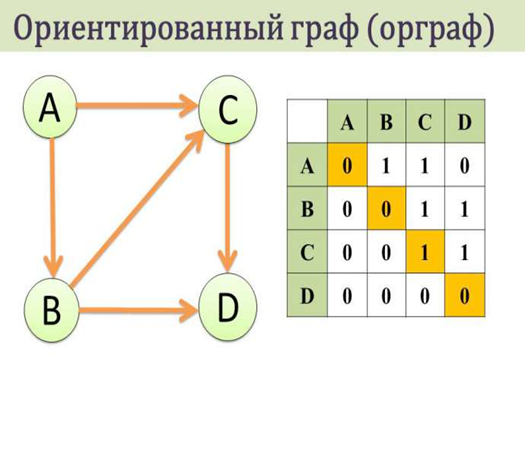
1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.

2. Неориентированный граф - это граф, в котором нет направления линий.

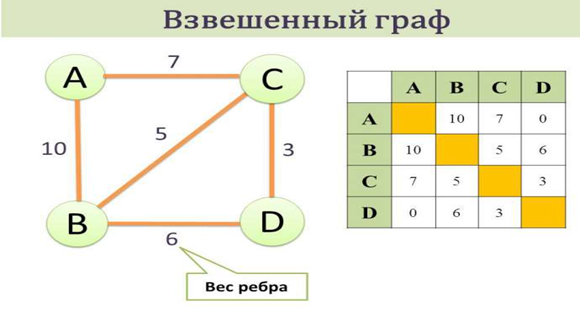
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация).

Задача 1.

Из лагеря вышли четыре туриста: Вася, Галя, Толя и Лена. Вася идет впереди Лены, Толя впереди Гали, а Лена впереди Толи. В каком порядке идут дети?

Попробуем вначале эту задачу решить без использования графа. При этом условие, что Толя идет впереди Гали придется вначале пропустить, т.к. неясно, они идут перед Васей и Леной или позади их. И только после прочтения последнего условия и установления, что Толя идет за Леной, можно определить месторасположение Гали.

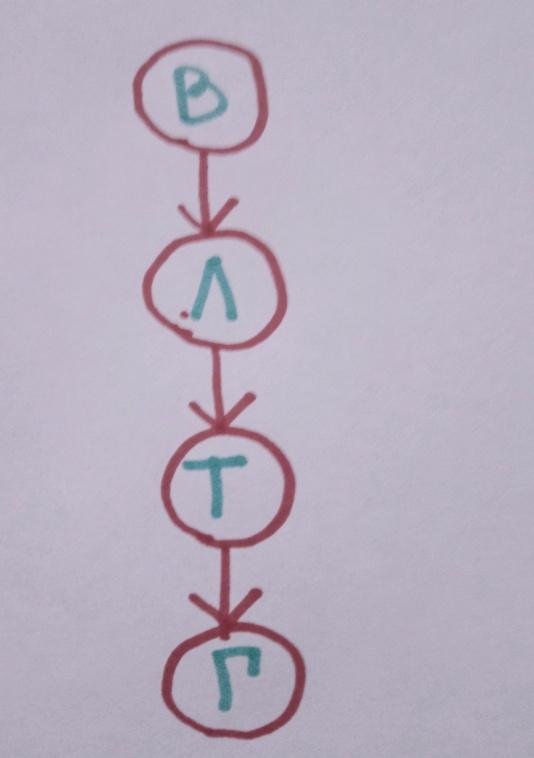
Когда же мы решаем эту задачу при помощи графов, нам лишь необходимо представить условие задачи на графе. Изобразим всех туристов точками, которые обозначим первыми буквами имен детей. В задаче рассматривается отношение “идти впереди”, поэтому стрелку будем ставить от впереди идущего к идущему вслед за ним. Вася идет впереди Лены, значит стрелку ставим от Васи к Лене. Толя впереди Гали – стрелку ставим от Толи к Гале. Также ставим стрелку от Лены к Толе, т.к. она идет впереди него. На графе видно, что первый идет Вася, за ним Лена, Толя и Галя идет последней.

Задача 2.

У Маши были родные сёстры и братья. Сестра Вероника родилась раньше сестры Кати, а сестра Катя родилась после Вероники. Никита родился после Вовы, т.е. Вова родился после Кати, а самый младший ребёнок семьи - Маша. Вопрос такой: кто самый старший ребёнок в семье? Кто родился третьим в семье Маши?

Составлять этот граф мы будем так:

1. Будем рисовать точки или кружочки друг за другом.

2. Затем соединим все точки (кружочки) линиями (т.е. линия будет идти от одной точки, кружочка горизонтально вниз к другой точке).

3. После того как мы нарисовали граф мы будем писать первые буквы имени тех, кто за кем родился начиная с Вероники по порядку их рождения.

Делается вывод, что таким способом (т.е. путём составления графа мы легко можем ответить на эти вопросы). Итак - самый старший ребёнок семьи - Вероника, а третьим родился Вова.

Задача 3.

У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?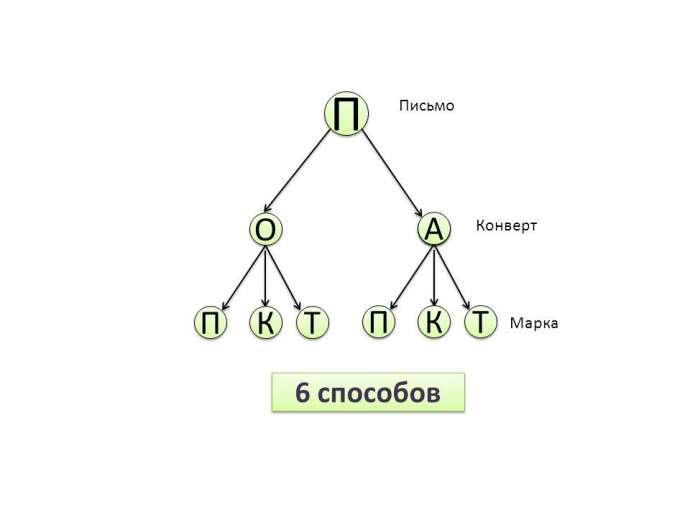

Задача 4.

В детском лагере отдыха в одной комнате живут четыре девочки: Маша, Валя, Таня и Галя. Две из них ровесницы. Известно, что Таня старше Маши, которая моложе Гали. Таня моложе Вали, которая старше Гали. Кто ровесницы?

Рассмотрим решение этой задачи при помощи графа. В задаче рассматриваются два отношения “быть младше” и “быть старше”. Выберем одно из них и построим граф отношения “быть старше”. При этом стрелку будем ставить от старшей девочки к младшей. По графу видно, что старше всех Валя, а Маша – младшая из девочек. Следовательно, ровесницы – это Галя и Таня.

В

Г

М

Задача 5. На урок в танцкласс пришли слон, волк и лев. Партнершами для них были выбраны мышка, белочка и лисичка. Помогите учителю расставить их в пары, если белочка боится, что ее съест волк, а слон - что он раздавит мышку. Сколько вариантов составления пар есть у учителя танцев? Перечислите их.

Составим граф:

Если такие простые задачи, в которых рассматривается множество, состоящее из небольшого числа элементов, еще можно решить без помощи графов, хотя такой способ решения является более сложным, то при решении задач на упорядочивание множества, состоящего из большого числа элементов, это становится практически невозможным.

Вот так легко и просто мы можем решать задачи с помощью графов. Подробно изучая эту тему, я узнал много интересного для меня. Графы – это замечательные математические объекты, с помощью, которых можно решать математические, логические и экономические задачи. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы упрощают решение задач в математике (но жалко, что использовать их можно не во всех задачах).