Получите свидетельство
Вход
Факультативное занятие по математике в 5 классе
ПРИЗНАКИ ДЕЛИМОСТИ
Цели и задачи
- Сформировать знание признаков делимости чисел.
- Отработать умения и навыки находить делители многозначных чисел.
- Расширить знания учащихся рассмотрением дополнительного материала по теме .
Деление чисел издавна считалось задачей, куда более трудной, чем умножение. Поэтому делить люди научились гораздо позже, чем умножать. Учёные – математики долго занимались поиском наиболее простого способа деления чисел. Один из них – деление «уголком», которым мы пользуемся сейчас, впервые появился в Европе в 10 веке и получил название «золотого деления». На деление уголком часто затрачивается много времени, а ведь возникают ситуации, когда нужно быстро определить, делится одно число на другое или нет. В этом помогают простые, легко запоминающиеся признаки.
Признак делимости — это правило, позволяющее быстро определить, является ли число кратным заранее заданному числу, без необходимости выполнять деление.
Выдающиеся математики, занимающиеся признаками делимости.
Леонардо Фибоначчи Блез Паскаль
(1170 – 1228 г.г.) (1623 – 1162 г.г.)
Признак делимости на 2.
- 67537 0 , 590 2 , 658 4 , 579 6 , 904956 8 –
чётные цифры.
Эти числа делятся на 2.
- 657 1 , 784 3 , 6789 5 , 90455 7 , 987658 9 .
1,3,5,7,9 – нечётные цифры.
Эти числа не делятся на 2.
0,2,4,6,8
Число делится на 2, если последняя цифра в записи этого числа
ЧЁТНАЯ.
2
0
3
4
5
6
7
8
9
Найди числа, которые делятся на 2 и щёлкни по ним мышкой.
ПОДСКАЗКА
350
30
429
243
1506
24
237
48
385
392
Найди числа, которые не делятся на 2 и щелкни по ним мышкой.
ПОДСКАЗКА
353
33
242
326
27
3305
270
669
372
777
Нечетные числа
Четные числа
1
Признак делимости на 3.
Если сумма цифр числа делится на 3 , то и число делится на 3 .
=
+
+
+
12
3
4
2
5
2
4
3
1
1
5
Признак делимости на 3.
3
+
+
=15
6
2
2
6
7
7
3
Какие цифры следует поставить вместо звездочек в
записи чисел, чтобы получившиеся числа делились
на 3 ?
2 * 5
2 5
5
3
0
1
2 5
8
6
4
2 5
7
2
9
4 6 *
46
9
5
0
1
46
6
8
4
46
7
2
3
8
Признак делимости на 4.
Если последние две цифры составляют число,
кратное 4 (или два нуля), то число делится на 4.
4
Примеры.
4
23 312
12
4
4
7 308
08
4
4
275 600
00
Признак делимости на 5 :
Если запись натурального числа оканчивается цифрой 0 или 5 , то это число делится без остатка на 5 .
СХЕМА ПРИЗНАКА: ХХХ 0 :5
ХХХ 5 :5
ПРИМЕР: 87 0 и 87 5 делятся без остатка на 5,
а числа 87 2 и 87 3 на 5 не делятся.
Какие числа, кратные 5, удовлетворяют неравенству
1 x
30
20
22
21
10
26
40
50
5
23
15
16
16
4
35
25
12
Признак делимости на 6 Если число кратно 3 и чётное, то оно делится на 6. 6=2*3
- 6 так как
7
4
4
1
-чётная цифра
3
=12
+
+
Признак делимости на 8.
Если последние три цифры составляют число,
кратное 8 (или три нуля), то число делится на 8.
Примеры.
8
8
8
8
3 008
008
8
75 000
000
8
7 848
848
8
8
8
8
92 024
3 640
024
640
Признак делимости на 9.
Если сумма цифр числа делится на 9 , то и число делится на 9
+
9
+
+
=18
4
5
5
4
8
9
1
1
8
Признак делимости на 9.
+
+
+
+
+
9
5
4
5
4
8
9
6
6
8
1
3
3
1
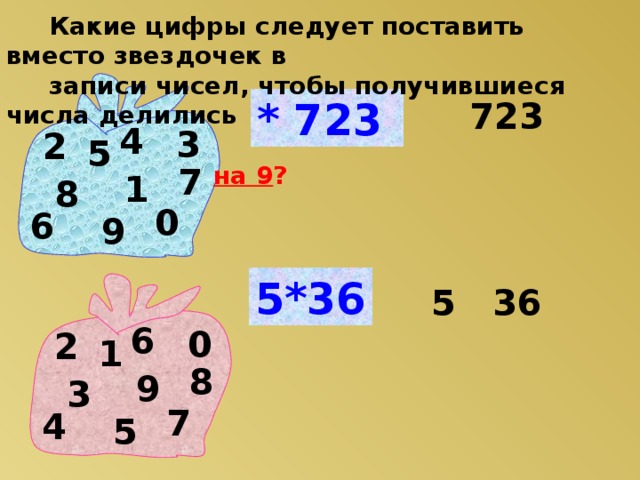
Какие цифры следует поставить вместо звездочек в
записи чисел, чтобы получившиеся числа делились
на 9 ?
* 723
723
4
3
2
5
7
1
8
0
6
9
5*36
5 36
.
6
0
2
1
8
9
3
7
4
5
16
Признак делимости на 10 :
Если запись натурального числа оканчивается цифрой 0 , то это число делится без остатка на 10.
СХЕМА ПРИЗНАКА: ХХХ 0 : 10
ПРИМЕР: 210 6 : 10=210(остаток 6 );
701 0 : 10=701
Признак делимости на 11.
Если сумма цифр числа, занимаемых нечетные места
и сумма цифр, занимаемых четные места, равны
или отличаются на число, кратное 11,
то число делится на 11.
Примеры.
+ + =15;
+ + =15
5
6
4
2
7
6
746 526
11
+ + =18;
+ + =7;
18–7=11
11
281 446
4
1
6
2
8
4
11
+ + + =28;
+ + + =6;
28–6=22
11
2
8
28 193 209
0
9
3
1
9
2
11
Признак делимости на 25.
Если последние две цифры составляют число,
кратное 25 (или два нуля), то число делится на 25.
Примеры.
25
25
25
325
25
25
8 375
75
25
25
25
7 350
50
25
275 600
00
Решите задачу: Фермер купил 25 коров. Можно ли утверждать, что его покупка стоит 874900 руб. 156375 руб. 100005 руб. 125330 руб. 948225 руб. (стоимость каждой коровы выражается натуральным числом).
ДА
ДА
НЕТ
НЕТ
ДА
Факультативное занятие "Признаки делимости" (540.1 KB)
0
1497
100
Нравится
0
