Ещё раз о решении уравнения вида аsinx + bcosx = c,
где а, в и с – некоторые числа, причем ав не равно 0 и с не равно 0.
Существует достаточно много способов его решения, но я предложил ввести замену x = 2t. В этом случае мы получим уравнение аsin 2t + bcos 2t = c. Применяя формулы двойного угла для синуса и косинуса, а также основное тригонометрическое тождество, получим следующее равенство: 2asin t cos t + b (cos2x – sin2x) = с(cos2x + sin2x). Раскроим скобки и приведем подобные члены: 2asin t cos t + (b – c) cos2t – (b + c) sin2t. Получили однородное тригонометрическое уравнение второй степени, уравнение (1). Так как корни уравнения вида cos2t = 0 не являются решением уравнения (1), то поделим на выражение cos2 t :

Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход


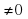 и с
и с 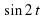 + b
+ b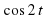 = c. Применяя формулы двойного угла для синуса и косинуса, а также основное тригонометрическое тождество, получим следующее равенство: 2a
= c. Применяя формулы двойного угла для синуса и косинуса, а также основное тригонометрическое тождество, получим следующее равенство: 2a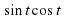 + b(
+ b(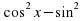 x) = с
x) = с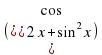 . Раскроим скобки и приведем подобные члены: 2a
. Раскроим скобки и приведем подобные члены: 2a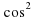 t – (b + c)
t – (b + c)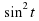 = 0. Получили однородное тригонометрическое уравнение второй степени, уравнение (1). Так как корни уравнения вида
= 0. Получили однородное тригонометрическое уравнение второй степени, уравнение (1). Так как корни уравнения вида 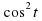 = 0 не являются решением уравнения (1), то поделим на выражение
= 0 не являются решением уравнения (1), то поделим на выражение 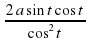 +
+ 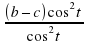 -
- 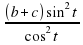 = 0 или (b + c)
= 0 или (b + c)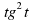 - 2a
- 2a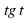 - (b – c) = 0.
- (b – c) = 0. 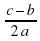 . Откуда получаем:
. Откуда получаем: 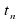 = arctg
= arctg 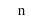 , n
, n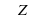 , значит серию решений можно записать так:
, значит серию решений можно записать так: 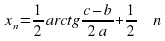 , n
, n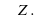









 Ещё раз о решении уравнения вида asinx + bcosx = c (18.81 КB)
Ещё раз о решении уравнения вида asinx + bcosx = c (18.81 КB)
 0
0 5709
5709 325
325 Нравится
0
Нравится
0






