ГАПОУ «Оренбургский областной медицинский колледж»
Методическая разработка
теоретического занятия для преподавателя
по дисциплине ОДБ.04 Математика
| для специальностей: | 31.02.02 Акушерское дело 34.02.01 Сестринское дело 33.02.01 Фармация |
на базе основного общего образования (база 9 классов)
Тема: «Элементы комбинаторики. Формула бинома Ньютона»
Оренбург 2018
РассмотренА и одобренА
на заседании
общеобразовательной ПЦК
Протокол №_________________
« __ » _________________ 2018г.
Председатель ПЦК
_________________ Лапина Н.В.
Автор: преподаватель математики ГАПОУ «ООМК» Данилова Е.В.
Учебно-методическая карта
Тема: «Статистическая обработка данных»
Тип занятия: комбинированный (усвоение новых знаний и первичное закрепление)
Форма проведения: теоретическое занятие
Продолжительность: 90 минут
Цели:
Образовательная:
добиться прочного усвоения знаний по теме;
познакомить с начальными представлениями о комбинаторике, соединениях (перестановках, сочетаниях, размещениях), формуле бинома Ньютона.
Студент должен иметь представление:
о табличном и графическом представлении данных.
Студент должен знать/понимать:
понятия: комбинаторика, факториал, перестановки, сочетания, размещения, конечное множество, бином Ньютона, биномиальные коэффициенты, треугольник Паскаля;
формулы: числа перестановок, сочетаний, размещений, бинома Ньютона;
свойства биномиальных коэффициентов;
метод перебора;
поочередный и одновременный выбор нескольких элементов из конечного множества.
Студент должен уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
понимания взаимосвязи учебного предмета с особенностями профессии и профессиональной деятельности, в основе которых лежат знания по данному учебному предмету.
Развивающая:
развивать исследовательскую культуру;
развивать навыки построения логической цепи рассуждений;
способствовать развитию кругозора, логического мышления, грамотной речи, внимания и памяти;
способствовать развитию умений оформлять результаты эксперимента в устной и письменной форме.
Воспитательная:
содействовать формированию коммуникативной компетенции (культуры общения, умения аргументировать свою точку зрения);
содействовать воспитанию интереса к математике.
Методическая:
структурировать теоретические знания по теме для более легкого восприятия информации студентами;
наглядно продемонстрировать перенос теоретических знаний на практику на примерах решения задач;
стимулировать познавательную и творческую активность студентов.
Основное содержание материала: Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Решение простейших комбинаторных задач методом перебора, а также с использованием известных формул.
Педагогические технологии:
личностно-ориентированное обучение;
технология проблемного обучения;
технология развивающего обучения.
Методы обучения:
словесный;
наглядный;
частично-поисковый;
объяснительно-иллюстративный;
проблемный;
аналитический;
исследовательский.
Формы организации контроля:
самоконтроль;
взаимоконтроль;
тестовый контроль.
Формы организации учебной деятельности:
коллективная;
индивидуальная.
Межпредметные связи с дисциплинами:
история;
генетика;
биология;
информатика.
Внутрипредметные связи:
числовые последовательности;
корни и степени;
теория вероятности;
теория множеств.
Оборудование:
классная доска, мел.
Оснащение:
дидактическое:
обучающее видео «Математические секреты треугольника Паскаля»;
тестовые задания.
методическое:
рабочая программа учебной дисциплины ОДБ.04 Математика;
тематический план;
учебно-методическая карта;
методическая разработка для преподавателя по теме «Элементы комбинаторики. Формула бинома Ньютона».
Виды самостоятельной работы:
аудиторная:
решение задач на перебор вариантов, на подсчет числа перестановок, сочетаний, размещений;
решение тестовых заданий.
внеаудиторная:
работа с дополнительными источниками информации;
составление бинома Ньютона при n3.
Предварительная подготовка студентов: подготовка сообщений.
Список литературы
Основная:
Математика: алгебра и начала математического анализа, геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / [Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачёва и др.]. – 5-е изд. – М. : Просвещение, 2018.
Дополнительная:
Бутузов В.Ф., Прасолов В.В. / Под ред. Садовничего В.А. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровень). Просвещение, 2014г.
Колягин Ю.М., Ткачёва M.B., Фёдорова Н.Н. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровень). Просвещение, 2015г.
Шарыгин И.Ф. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый уровень). Дрофа, 2014г.
Литература для студентов:
Математика: алгебра и начала математического анализа, геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / [Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачёва и др.]. – 5-е изд. – М. : Просвещение, 2018.
План занятия
Вводная часть – 10-12 мин.
Организационный момент – 1-2 мин.
Сообщение темы занятия, вовлечение обучающихся в процесс целеполагания, мотивация – 3-4 мин.
Активизация опорных знаний – 5-7 мин.
Основная часть (изучение нового теоретического материала) – 50-55 мин.
Историческая справка – 8-10 мин.
Возникновение комбинаторики как науки.
Элементы комбинаторики – 28-30 мин.
общие правила комбинаторики;
перестановки;
размещения;
сочетания.
Бином Ньютона – 13-15 мин.
формула бинома Ньютона;
свойства биномиальных коэффициентов;
треугольник Паскаля.
Закрепление материала – 23-25 мин.
Решение задач – 15-17 мин.
Тестовый контроль – 10-12 мин.
Рефлексия и подведение итогов – 2-3 мин.
Домашнее задание – 1-2 мин.
СВР: Составление бинома Ньютона при n3.
План-конспект занятия
Вводная часть – 10-12 мин.
Организационный момент – 1-2 мин.
Проверка присутствующих студентов и их готовности к занятию.
Сообщение темы занятия, вовлечение обучающихся в процесс целеполагания, мотивация – 3-4 мин.
Вопросы студентам:
Можно ли подсчитать число всех возможных комбинаций, которые можно составить из небольшого количества элементов?
А если элементов будет значительно больше и сколько времени на это потребуется?
Можно ли возвести двучлен в достаточно большую степень, например десятую, не перемножая при этом последовательно скобки?
Активизация опорных знаний – 5-7 мин.
Вспомнить факториалы.
n! = 1∙2∙3∙…∙n
0! = 1
Решение задачи на перебор вариантов.
Задача:
На должности медсестры процедурного кабинета, участковой медсестры и медсестры физиотерапевтического кабинета претендуют Иванова, Громова и Орлова. Назовите возможные варианты распределения должностных мест.
Ответ:
Вариант1: 1) Иванова, 2) Громова, 3) Орлова.
Вариант2: 1) Иванова, 2) Орлова, 3) Громова.
Вариант3: 1) Орлова, 2) Иванова, 3) Громова.
Вариант4: 1) Орлова, 2) Громова, 3) Иванова.
Вариант5: 1) Громова, 2) Орлова, 3) Иванова.
Вариант6: 1) Громова, 2) Иванова, 3) Орлова.
Решение задачи методом перебора вариантов занимает достаточно большое количество времени. Как можно было решить ее быстрее мы узнаем чуть позже на сегодняшнем занятии.
Основная часть (изучение нового теоретического материала) – 50-55 мин.
Историческая справка – 8-10 мин.
При решении многих практических задач часто приходится имеющиеся предметы (элементы) соединять в разные наборы (комбинации). Задачи, которые рассматривают такие соединения, и находится число различных соединений, называют комбинаторными.
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос «сколькими способами».
Сообщение студентов «Возникновение комбинаторики как науки».
Элементы комбинаторики – 28-30 мин.
Общие правила комбинаторики
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами умножения и сложения.
Правило суммы
Если некоторый объект А можно выбрать m способами, а объект В - k способами (не такими, как А), то объект либо А, либо В можно выбрать m + k способами.
Пример:
В ящике имеется n разноцветных шариков. Произвольным образом вынимаем один шарик. Сколькими способами это можно сделать? Конечно, n способами.
Теперь эти n шариков распределены по двум ящикам: В первом m шариков, во втором k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами это можно сделать? Из первого ящика шарик можно вытянуть m различными способами, из второго k: различными способами, всего n = m + k способами.
Правило произведения
Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора А) k способами, то пары объектов А и В можно выбрать m·k способами.
Задача:
В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
По правилу умножения двух девушек можно выбрать 14 ·13 = 182 способами, а двух юношей 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студентов или студенток. Согласно правилу сложения таких способов выбора будет 182 + 30 = 212.
Задача:
Сколько можно записать двузначных чисел в десятичной системе счисления?
Поскольку число двузначное, то число десятков (m) может принимать одно из девяти значений: 1,2,3,4,5,6,7,8,9. Число единиц (k) может принимать те же значения и может, кроме того быть равным нулю. Отсюда следует, чтоm = 9, а k= 10. Всего получим двузначных чисел n = m ·k = 9·10 =90.
Следствие
Правило произведения справедливо и для любого конечного числа объектов.
Если некоторый объект Аi (i = 1, 2, … , n) можно выбрать Кi (i = 1, 2, … , n) способами (причем, каждый следующий объект выбирается независимо от выбора предыдущего объекта), то объекты А1, А2, … , Аn можно выбрать k = k1 · k2 ·…· kn способами.
Например, сколькими способами можно составить трехзначное число, делящееся на 5? Число имеет три позиции, каждую из которых мы назовем событием:
событие А1 –число сотен, их можно выбрать k1 =9 (все цифры, кроме 0) способами;
событие А2 – число десятков, их можно выбрать k2 = 10 (все цифры, включая 0) способами;
событие А3 – число единиц, которым удовлетворяет только две цифры: 0 и 5, следовательно, k3 = 2. Таким образом, всего получаем n = k1 · k2 · k3 = 9 · 10 · 2 = 180 чисел.
Перестановки
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
Рn = n · (n - 1) · (n – 2) · … · 2 · 1 = n!
Пример:
Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Решение: ![]() .
.
Пример:
Порядок выступления семи участников на студенческой конференции определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение:
Каждый вариант жеребьевки отличается только порядком участников, то есть является перестановкой из 7 элементов. Их число находится
![]() .
.
Пример:
К кассе за получением денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?
Решение:
Очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырех человек, их число равно
![]()
Размещения
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо их порядком, либо составом элементов.
Число всех возможных размещений рассчитывается
![]()
Пример:
Сколько можно составить сигналов из 6 флажков различного цвета, взятых по два?
Решение: ![]()
Пример:
Расписание одного дня состоит из пяти уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
Решение:
Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания находят по формуле
![]()
Сочетания
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
![]()
Пример:
Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
Решение: ![]()
Пример:
В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение:
Каждая партия играется двумя участниками из 16 и отличается только составом пар участников, то есть представляет собой сочетание из 16 элементов по два
![]()
Пример:
Имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать три штамма. Сколькими способами можно это сделать?
Решение:
Способы отбора считаются различными, если каждый отобранный штамм различается хотя бы одним элементом. Это число
![]()
То есть имеется 20 способов.
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
![]()
Бином Ньютона – 13-15 мин.
Формула бинома Ньютона
Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:
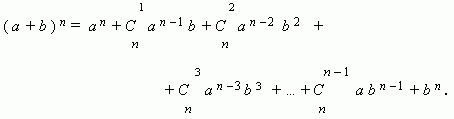
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
Пример 1: 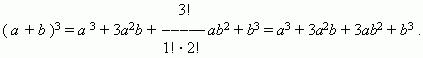
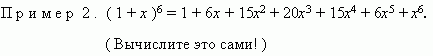
Числа ![]() называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Свойства биномиальных коэффициентов
Сумма коэффициентов разложения ( a + b ) n равна 2 n .
Коэффициенты членов, равноудалённых от концов разложения, равны.
Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна ![]()
Треугольник Паскаля
Просмотр обучающего видео «Математические секреты треугольника Паскаля».
Биномиальные коэффициенты можно вычислить, применяя только сложение, если пользоваться треугольником Паскаля:
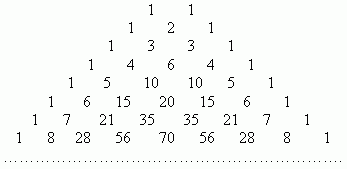
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение ( a + b )7 , мы можем получить результат моментально, используя таблицу:
![]()
Закрепление материала – 23-25 мин.
Решение задач – 15-17 мин.
Замечание: При решении задач по комбинаторике следует обращать внимание, учитывается ли порядок в сочетаниях. Если порядок учитывается, то есть составляются упорядоченные множества, то это – размещения. Если порядок не учитывается, то есть составляются множества, то это – сочетания.
Типичные задачи, в которых обычно путаются студенты
| Сочетания | Размещения |
| 1. Сколько рукопожатий получится, если здороваются 5 человек? | 1. Сколькими способами пять человек могут обменяться фотографиями? |
| Перестановки | |
| 1. Сколькими способами n человек могут сесть на одной скамейке? | 2. Сколькими способами n человек могут сесть за круглым столом? |
Задачи:
Сколько различных экзаменационных комиссий по 3 человека можно составить, если на кафедре 20 преподавателей?
Сколькими способами можно окрасить трехкомнатную квартиру (каждая комната окрашивается одной краской, все комнаты окрашиваются в разные цвет), если имеется 10 различных красок?
Сколькими способами можно расставить 5 книг на полке?
Тестовый контроль – 10-12 мин.
ТЕСТ №1
1. Сколькими способами можно выбрать 3 плитки шоколада из имеющихся 5 плиток?
А) 15; В) 60; С) 45; D) 120.
2. На пяти карточках написаны числа 1, 2, 3, 4, 5. Сколько различных трехзначных чисел можно из них составить?
А) 25; В) 60; С) 20; D) 6.
3. Составить из трех букв А, В и С все сочетания по две буквы.
А) 12; В) 9; С) 6; D) 68.
4. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно
сделать?
А) 190; С) 120; С) 95; D) 150.
5. Из 10 роз и 8 георгинов нужно составить букет так, чтобы в нем было 2 розы и 3 георгина. Сколькими способами это можно сделать?
А) 3220; В) 1250; С) 2520; D) 1260.
ТЕСТ №2
1. Сколько различных комбинаций может выпасть в спортлото "6 из 45" ?
А) 75 230; В) 8 145 060; С) 10 230 000; D)50 250 018 .
2. Составить все размещения из трех букв А, В, С.
А) 6; В) 8; С) 12; D) 15.
3. Сколькими способами можно группу из 15 учащихся разделить на две группы так, чтобы в одной группе было 4, а в другой - 11 человек?
А) 968; В) 1200; С) 1456; D) 1365.
4. Сколькими способами можно расставить 8 томов энциклопедии на книжной полке так, чтобы первый и второй тома не стояли рядом?
А) 26 854; В) 32 278; С) 30240; D) 25 234.
5. В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?
А) 1956; В) 1236; С) 2160; D) 2112.
ОТВЕТЫ
| № | 1 | 2 | 3 | 4 | 5 |
| Тест№1 | В | В | С | А | А |
| Тест№2 | В | А | D | А | С |
Рефлексия и подведение итогов – 2-3 мин.
Что нового узнали на занятии?
Что осталось недопонятым?
Домашнее задание – 1-2 мин.
СВР: Составление бинома Ньютона при n3.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Элементы комбинаторики. Бином Ньютона (73.51 KB)
Элементы комбинаторики. Бином Ньютона (73.51 KB)
 0
0 945
945 11
11 Нравится
0
Нравится
0




