Элективны курс матемтического профиля «Функциональная зависимость»
Цель курса
1. Создать условия для повышения уровня математической подготовки учащихся.
2. Научить разнообразным методам решения математических задач.
3. Установить взаимосвязи между различными темами курса математики.
Задачи курса
Развитие интереса к математике, творческих способностей учащихся на наглядном материале
2. Формирование функциональных представлений учащихся на наглядном материале
3. Овладение системой знаний и умений по использованию свойств функции для решения различных задач в объеме необходимом для успешной сдачи ЕГЭ и дальнейшего обучения в вузе
Ожидаемые результаты
Знать основные свойства функций;
Уметь читать графики функций;
Уметь применять свойства функций при решении нестандартных уравнений и неравенств;
Уметь использовать геометрический и физический смысл производной в решениях задач.
Формы занятий
Лекции, практикумы, семинары, зачеты.
Учебно-тематический план
| Тема | Кол-во часов |
| 1.Понятие функции | 1 |
| 2.Оснеовыне свойства функции | 1 |
| 3.Графики основных элементарных функций | 1 |
| 4.Свяь между свойствами функции и ее графиком | 2 |
| 5.Использование графиков функции при решении неравенств | 2 |
| 6.Функциональный метод решения уравнений | 10 |
| 7. Предел функции | 2 |
| 8. Бесконечно малые и бесконечно большие | 1 |
| 9.Осонвные теоремы о пределах | 3 |
| 10.Непрерывность функции | 3 |
| 11. Производная функции | 3 |
| 12.Геометрпический и физический смысл производной | 3 |
| 13.Зачет | 2 |
| Итого | 34 |
Содержание курса
1.Понятие функции.
Определение функции , простейшие функциональные зависимости.
2. Основные свойства функций.
Область определения, множества значений, нули, промежутки знакопостоянства, четность, периодичность, монотонность, экстремумы, наибольшее и наименьшее значения.
3.Графики основных элементарных функций
y=kx+=b; y=
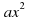 +bx+c;y=
+bx+c;y=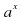 ;y=
;y= x;y=sin x;
x;y=sin x;y=cos x; y=tg x; y=ctg x; y=arcsin x др.
4. Связь между свойствами функций и их графиками.
Чтение графика функции
5. Использование графиков функции при решении неравенств.
Метод областей.
6.Функциаональный метод решения уравнений
Использование понятий области определения, области значения(метод оценки), свойств монотонности, четности и нечетности, периодичности функций.
7.Предел функции
Определение предела, односторонние пределы функции.
8.Бесконечно малые и бесконечно большие.
Определения и основные теоремы.
9. Основные теоремы о пределах .
Теоремы о пределе суммы, о пределе произведения, следствия о постоянном множителе, о пределе степени, замечательные пределы
10. Непрерывность функции.
Определение непрерывной функции, точки разрыва, непрерывность основных элементарных функции, основные теоремы, раскрытие неопределенностей
11. Производная функции.
Зависимость между непрерывностью и дифференцируемостью функции.
12. Геометрический и физический смысл производной.
Использование понятий при решении задач физики и алгебры.
Примерные задания зачета
1. На каком множестве совпадают функции: y=
 и y=
и y= -3?
-3?1) (
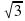 ;+∞) 2)[
;+∞) 2)[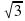 ;+∞) 3) (-∞;-
;+∞) 3) (-∞;-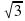 ) 4) (-∞;-
) 4) (-∞;-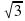 ) Ų (
) Ų (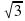 ;+∞)
;+∞) 2. Функция у=f(x) задана на промежутке [-6;5]. Решите неравенство f ( x-1) ≤0 на промежутке [-6;5].
1) [-4;-2] Ų [1;3] 2)[-3;-1]Ų[2;4] 3)[-5;-3]Ų[0;2] π
4) [-6;-4]Ų[-2;1]Ų[3;5]
3.Укажите число целых значений функции у=3-
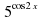
1) 3 2)5 3)4 4)1
4.Дана функция у=2
 -54 х+4. Найдите расстояние между абсциссами точек графика этой функции, касательные в которых параллельны прямой у=12
-54 х+4. Найдите расстояние между абсциссами точек графика этой функции, касательные в которых параллельны прямой у=12
1)4 2)3 3)8 4)6
5. Функция у=f(x) определена на всей числовой прямой и является четной периодической с периодом, равным6. На отрезке [0;3] функция у=f(x) задана равенством f(x)= -
 +4x-1. Сколько нулей имеет функция у=f(x) на отрезке [-3;5]?
+4x-1. Сколько нулей имеет функция у=f(x) на отрезке [-3;5]?6.Решите уравнение 5
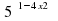 =sin πx.
=sin πx.7.Решите неравенство In(x-2)≥x-3
Определить число корней уравнения
 –a=
–a=
Литература
Лысенко Ф.Ф., Калашников В.Ю. и др. Подготовка к ЕГЭ, подготовка к вступительным экзаменам. Ростов-на-Дону: Сфинкс,2007.
Ткачук В.В. Математика- абитуриенту.
-М. :МЦНМО,1997
Томашевич Я.И. О нестандартных приемах решения неравенств. М/ш №2, 1969
Ковалева Г.И., Конкина Е.В. Функциональный метод решения уравнений и неравенств . М.,2008
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. Наука 1999
Локоть .В.В. Применение свойств функций, преобразование неравенств. М.,2007.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Элективный курс "Функциональная зависимость" (24.17 KB)
Элективный курс "Функциональная зависимость" (24.17 KB)
 0
0 310
310 4
4 Нравится
0
Нравится
0


