Эффективные алгоритмы численного решения алгебраических уравнений, расчета производных, решение систем линейных алгебраических и дифференциальных уравнений в Scilab

ФБГОУВПО «Мордовский Государственный педагогический институт им. М.Е.Евсевьева»

Физико-математический факультет

Кафедра информатики и вычислительной техники

РЕФЕРАТ

Эффективные алгоритмы численного решения

алгебраических уравнений, расчета производных, решение

систем линейных алгебраических и дифференциальных

уравнений в Scilab

Выполнил: студент группы МДФ-113

физико-математического факультета

Атряхин Андрей Андреевич

Проверила: Кормилицына Т.В.

Саранск 2017

Введение

С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).

Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.

Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.В системе доступно множество инструментов:

• 2D и 3D графики, анимация

• Линейная алгебра, разреженные матрицы (sparse matrices)

• Полиномиальные и рациональные функции

• Интерполяция, аппроксимация

• Симуляция: решение ОДУ и ДУ

• Scicos: гибрид системы моделирования динамических систем и симуляции

• Дифференциальные и не дифференциальные оптимизации

• Обработка сигналов

• Параллельная работа

• Статистика

• Работа с компьютерной алгеброй

• Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW

Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.

Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.

Для численных расчётов используются библиотеки Lapack, LINPACK, ODEPACK , Atlas и другие.

В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.

Программа доступна для различных операционных систем, включая Linux, Microsoft Windows и Mac OS X. Возможности Scilab могут быть расширены внешними программами и модулями, написанными на разных языках программирования. Программа имеет открытый исходный код, что позволяет как свободное коммерческое использование и распространение неизменённых версий, так и некоммерческое распространение измененных версий, которые должны включать в себя исходный код. Для коммерческого распространения измёненных версий необходимо согласование с INRIA.

Начиная с версии 5.0 программа распространяется под совместимой с GNU GPL 2 лицензией CeCILL.Отличия от некоторых коммерческих программ:

• Бесплатность.

• Свободность (с версии 5.0).

• Маленький размер — дистрибутив 4 версии занимал менее 20 МБ против более чем двухгигабайтного пакета MATLAB. Инсталлятор 5 версии (5.4.1) увеличился в объёме до 117 МБ.

• Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Windows (в UNIX и Windows версиях MatLab-а эта возможность присутствует тоже). Это позволяет производить автоматизированные вычисления, есть пакетный режим.

1. Алгебраические уравнения

Любое уравнение P(x)=0, где P(x) это многочлен, отличный от нулевого, называется алгебраическим уравнением (полиномом относительно переменных x. Всякое алгебраическое уравнение относительно x можно записать в виде

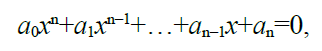
где a0≠0, n1 и ai – коэффициенты алгебраического уравнения n–й степени. Например,

линейное уравнение это алгебраическое уравнение первой степени, квадратное – второй,

кубическое – третьей и так далее.

Для определения алгебраического уравнения в Scilab существует функция

poly(a,"x", ["fl"]), где a это число или матрица чисел, x – символьная переменная, fl – строковая переменная, определяющая способ задания полинома. Строковая переменная fl может принимать только два значения – “roots” или “coeff” (соответственно “r” или “c”). Если fl= c, то будет сформирован полином с коэффициентами, хранящимися в параметре a. Если же fl= r, то значения параметра a воспринимаются функцией как корни, для которых необходимо рассчитать коэффициенты соответствующего полинома. По умолчанию fl= r.

Рассмотрим несколько примеров формирования полиномов.

Листинг 1.1 отражает создание полинома p, имеющего в качестве корня тройку, и

полинома f с коэффициентом 3.

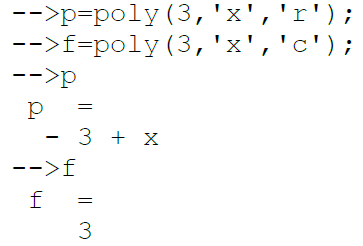
Листинг 1.1.

На листинге 1.2 приведены примеры создания более сложных полиномов.

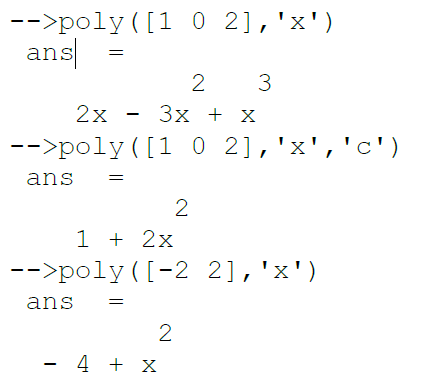
Листинг 1.2

Листинг 1.3 содержит примеры операций с полиномами.

Листинг 1.3

Решим несколько алгебраических уравнений.

ЗАДАЧА 1.1. Найти корни полинома 2x4–8x3+8x2–1=0.

Для решения этой задачи необходимо задать полином р. Сделаем это при помощи функции

poly, предварительно определив вектор коэффициентов V. Обратите внимание, что в уравнении отсутствует переменная x в первой степени, это означает, что соответствующий коэффициент равен нулю. Отыскание корней полинома при помощи функции roots(p) приведено в листинге 1.4. Графическое решение, показанное на рис. 1.1 позволяет убедится, что корни найдены верно.

Листинг 1.4

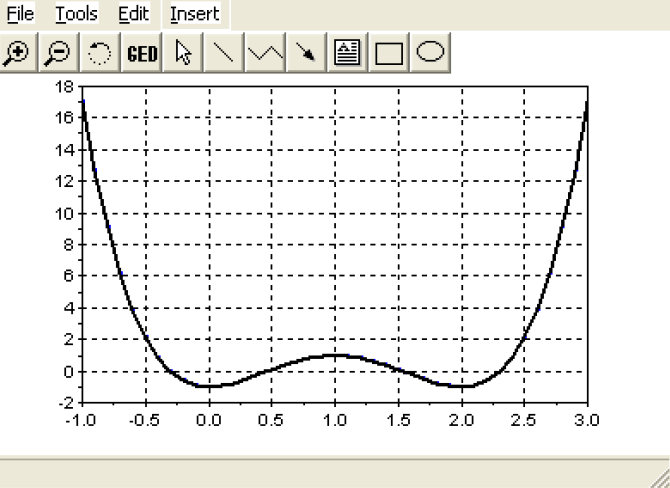
Рис. 1.1. График функции y=2x4–8x3+8x2–1

ЗАДАЧА 1.2. Найти корни полинома x3+0.4x2+0.6x –1=0.

Решение этой задачи аналогично решению предыдущей. Разница заключается в способе вызова необходимых для этого функций. Не трудно заметить (листинг 1.5), что полином имеет один действительный и два комплексных корня, в отличии от полинома из задачи 1.1, в котором все корни действительные. Рис. 1.2 подтверждает это.

Листинг 1.5

ЗАДАЧА 1.3. Найти решение уравнения y(x)=0, если y(x)=x4–18x2+6.

Листинг 1.6 демонстрирует решение этой задачи. Обратите внимание на способ определения полинома.

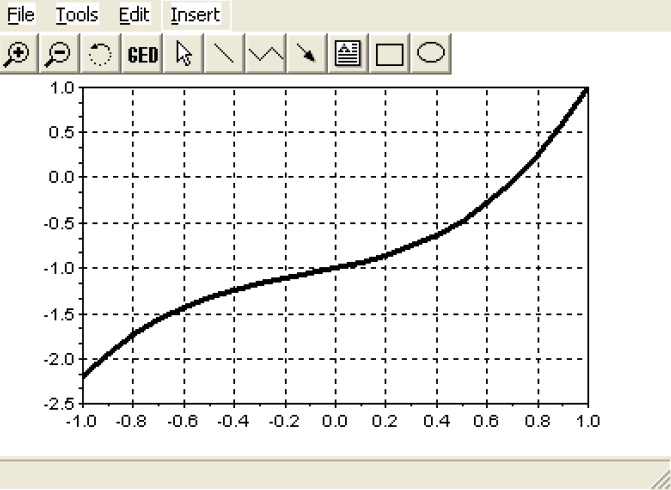
Рис. 1.2.График функции y= x3+0.4x2+0.6x –1

Листинг 1.6

В Scilab существует функция fsolve(x0,f), которую так же можно применить для решения алгебраических уравнений. Подробно эта функция будет описана далее, так как ее можно использовать для решения нелинейных уравнений, отличных от алгебраических, и для решения систем линейных и нелинейных уравнений.

ЗАДАЧА 1.4. Найти решение уравнения y(x)=0, если y(x)=x5–x3+1.

Решим эту задачу при помощи функции fsolve(x0,f), где x0 – начальное приближение, f – функция, описывающая левую часть уравнения y(x)=0. Листинг 1.7 содержит ход решения задачи. В первой строке происходит определение функции y(x) в виде исходного полинома.

Во второй, вызывается команда fsolve(-2,y), для отыскания корней функции y. В качестве начального приближения задано число –2, так как не трудно определить (рис. 1.3), что полином имеет единственный действительный корень, в интервале от –2 до –1.

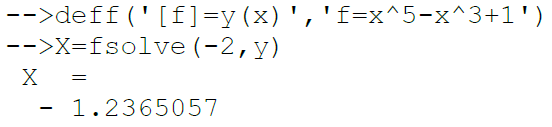
Листинг 1.7

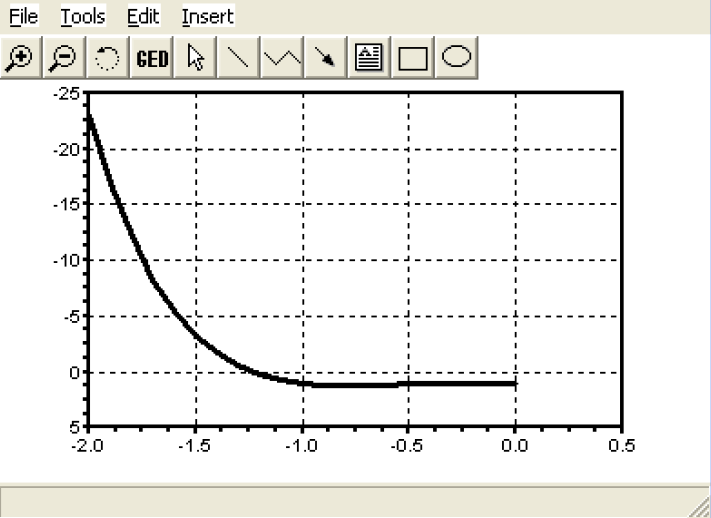
Рис. 1.3.График функции y(x)=x5–x3+1= x3+0.4x2+0.6x –1

Заметим, что заданное уравнение, кроме действительно корня, имеет и мнимые. Для отыскания всех корней полинома используйте функцию roots (листинг 1.8).

Листинг 1.8

1. Вычисление производной функции в точке. Приближенное вычисление частных производных.

Более универсальной командой дифференцирования является команда

g=numdiff(fun,x)

Здесь fun - имя функции, задающей выражение для дифференцирования. Функция должна быть задана в виде y=fun(x [,p1,p2,..pn]), где x - переменная по которой будет проводится дифференцирование. Если параметры p1,p2,..pn присутствуют в описании функции, то должны быть обязательно определены при вызове, например так:

g=numdiff(list(fun,p1,p2,..pn),x).

Результат работы функции - матрица

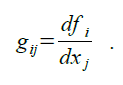
Рассмотрим несколько примеров.

ЗАДАЧА 2.1. Вычислить f'(1), если f(x)=(x+2)3+5x. Решение показано в листинге 2.1.

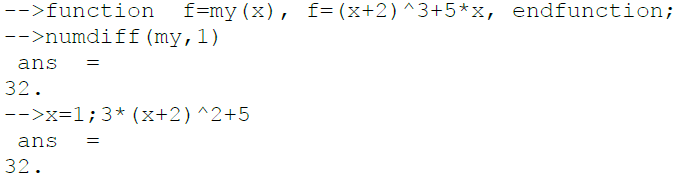
Листинг 2.1

ЗАДАЧА 2.1. Вычислить f'(x) в точках 0, 1, 2, 3 для f(x)=(x+2)3+5x (листинг 2.2).

Листинг 2.2

ЗАДАЧА 2.2. Задана функция многих переменных

Вычислить

в точке (1, 2, 3). Листинг 2.3 содержит решение задачи.

Листинг 2.3

1. Решение систем линейных алгебраических уравнений

Система m уравнений с n неизвестными вида

a11x1+a12x2+...+a1nxn=b1,

a21x1+a22x2+...+a2nxn=b2,

. . . . . . . . . . . . . . . . . . . . .

am1x1+am2x2+...+amnxn=bm,

называется системой линейных уравнений, причем xj – неизвестные, aij – коэффициенты при неизвестных, bi – свободные коэффициенты (i=1..m, j=1..n). Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A∙x=b, где x={xj} – вектор неизвестных, A={aij} – матрица коэффициентов при неизвестных или матрица системы, b={bi} – вектор свободных членов системы или вектор правых частей (i=1..m,

j=1..n). Совокупность всех решений системы (x1, x2,..., xn), называется множеством решений или просто решением системы.

ЗАДАЧА 3.1. Решить СЛАУ при помощи правила Крамера:

2x1+ x2–5x3+ x4=8,

x1–3x2 –6x4=9,

2x2– x3+2x4=-5,

x1+4x2–7x3+6x4=0.

Правило Крамера заключается в следующем. Если определитель Δ=detA матрицы системы из n уравнений с n неизвестными A∙x=b отличен от нуля, то система имеет единственное решение x1, x2,..., xn, Определяемое по формулам Крамера xi=Δi/Δ, где Δi – определитель матрицы, полученной из матрицы системы А заменой i–го столбца столбцом свободных членов b. Текст файла–сценария с решением задачи по формулам Крамера приведен в листинге 3.1.

Листинг 3.1

Результаты работы S–файла показаны в листинге 3.1.

Листинг 3.2

ЗАДАЧА 3.2. Решить СЛАУ из задачи 1 методом обратной матрицы.

Метод обратной матрицы: для системы из n линейных уравнений с n неизвестными A∙x=b, при условии, что определитель матрицы А не равен нулю, единственное решение можно представить в виде x=A-1∙b5.

Текст файла–сценария в листинге 3.3, результаты его работы в листинге 3.4.

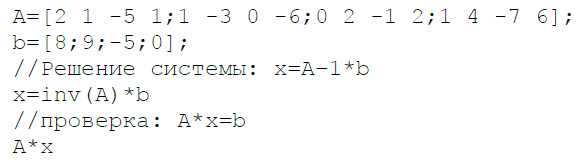
Листинг 3.3

Результаты работы S–файла

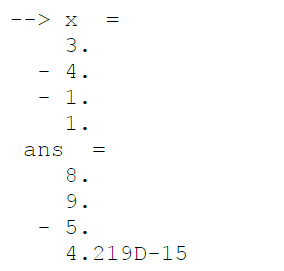
Листинг 3.4

ЗАДАЧА 4. Решить систему линейных уравнений методом Гаусса:

2x1– x2+5x3=0,

3x1+2x2–5x3=1,

x1+ x2–2x3=4.

Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к эквивалентной системе, которая решается проще, чем исходная система.

Метод Гаусса состоит из двух этапов. Первый этап это прямой ход, в результате которого расширенная матрица6 системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число отличное от нуля и сложение уравнений) приводится к ступенчатому виду. На втором этапе (обратный ход) ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица.

Последний, n+1 столбец этой матрицы содержит решение системы линейных уравнений.

Листинг 3.5 представляет текст файла–сценария, а листинг 3.36 результат работы S–файла.

Листинг 3.5

Листинг 3. 6

1. Решение обыкновенных дифференциальных уравнений

Дифференциальным уравнением n-го порядка называется соотношение вида (1.1)

Решением дифференциального уравнения является функция x(t), которая обращает уравнение в тождество.

Системой дифференциальных уравнений n-го порядка называется система вида:

(1.2)

Решение системы - вектор который обращает уравнения системы (1.2) в тождества:

(1.3).

Дифференциальные уравнения и системы имеют бесконечное множество решений, которые отличаются друг от друга константами. Для однозначного определения решения требуется задать дополнительные начальные или граничные условия. Количество таких условий должно совпадать с порядком дифференциального уравнения или системы. В зависимости от вида дополнительных условий в дифференциальных уравнениях различают: задачу Коши – все дополнительные условия заданы в одной (чаще начальной) точке интервала; краевую задачу – дополнительные условия указаны на границах интервала.

Большое количество уравнений может быть решено точно. Однако есть уравнения, а особенно системы уравнений, для которых точное решение записать нельзя. Такие уравнения и системы решают при помощи численных методов. Так же численные методы применяют, если для уравнений с известным аналитическим решением требуется найти числовое значение при определенных исходных данных.

Для решения дифференциальных уравнений и систем в Sciab предусмотрена функция:

для которой, обязательными входными параметрами являются:

y0 – вектор начальных условий;

t0 – начальная точка интервала интегрирования;

t – координаты узлов сетки, в которых происходит поиск решения;

f – внешняя функция, определяющая правую часть уравнения или системы уравнений (1.2);

y – вектор решений (8.3).

Таким образом, для того чтобы решить обыкновенное дифференциальное уравнение вида

необходимо вызвать функцию y=ode(y0,t0,t,f).

Рассмотрим необязательные параметры функции ode:

type – параметр с помощью которого можно выбрать метод решения или тип решаемой задачи, указав одну из строк:

adams- применяют при решении дифференциальных уравнений или систем методом прогноза-коррекции Адамса;

stiff- указывают при решении жестких задач;

rk- используют при решении дифференциальных уравнений или систем методом Рунге_Кутта четвертого порядка;

rkf- указывают при выборе пятиэтапного метода Рунге_Кутта четвертого порядка;

fix- тот же метод Рунге_Кутта, но с фиксированным шагом;

rtol,atol - относительная и абсолютная погрешности вычислений, вектор, размерность которого совпадает с размерностью вектора y, по умолчанию rtol=0.00001,

atol=0.0000001 , при использовании параметров rkfиfixrtol=0.001,

atol=0.0001 ;

jac – матрица, представляющая собой якобиан правой части жесткой системы дифференциальных уравнений, задают матрицу в виде внешней функции вида J=jak(t,y);

w,iw – векторы, предназначенные для сохранения информации о параметрах интегрирования, которые применяют для того, чтобы последующие вычисления выполнялись с теми же параметрами.

Рассмотрим использование функции на примере следующих задач.

ЗАДАЧА 4.1. Решить задачу Коши

Перепишем уравнение следующим образом:

Далее представим его в виде внешней функции, так как показано в листинге 4.1 и применим функцию y=ode(x0,t0,t,f), в качестве параметров которой будем использовать

f – ссылка на предварительно созданную функцию f(t,x);

t – координаты сетки;

x0,t0 – начальное условие x(0)=1.5;

y – результат работы функции.

График, моделирующий процесс, описанный заданным уравнением, представлен на

рис.8.1.

Листинг 4.1

Рис. 4.1. Решение дифференциального уравнения из задачи 8.1

ЗАДАЧА 4.2. Решить задачу Коши

на интервале [0; 10].

Листинг 4.2 содержит функцию, описывающую заданную систему обыкновенных дифференциальных уравнений и команды Sciab необходимые для ее численного и графического решения (рис.4.2).

Листинг 8.2

Рис. 4.2. Решение задачи 4.2

Рис. 4.3. Графическое решение жесткой системы

ЗАДАЧА 4.3. Найти решение задачи Коши для следующей жесткой системы:

Решение системы показано в листинге 8.3. Графическое решение показано на рис. 8.3.

Листинг 4.3

ЗАДАЧА 4.4. Решить нелинейную жесткую систему дифференциальных уравнений:

На рис. 4.4 показано решение системы на интервале [0; 2]. Команды Sciab необходимые

для достижения этого решения приведены в листинге 4.4.

Рис. 4.4. Решение жесткой нелинейной системы

Листинг 4.4

ЗАДАЧА 4.5. Решить следующую краевую задачу

на интервале [0.25; 2].

Преобразуем уравнение в систему, сделав замену

Составим функцию вычисления системы и решим ее так, как показано в листинге 4.5. График решения приведен на рис. 4.5.

Листинг 4.5

Рис.4.5. Решение задачи 4.5

Заключение

На основе анализа теории и примеров можно сделать вывод, что Scilab становится не просто «вычислялкой» отдельных небольших примеров, а настоящей «средой программирования с математическим уклоном», позволяющей создавать свои собственные математические «типы данных» — числовые системы, функционалы — и полноценные программные модули, которые могут использовать весь встроенный (или также собственноручно достроенный) функционал Scilab.

Scilab — мощный открытый пакет прикладных математических программ (система компьютерной математики) для инженерных и научных расчётов.

Система позволяет:

• решать задачи линейной алгебры;

• решать нелинейные уравнения и системы;

• решать задачи оптимизации;

• дифференцировать и интегрировать;

• решать обыкновенные дифференциальные уравнения и системы.

• обрабатывать экспериментальные данные (интерполяция и аппроксимация, метод наименьших квадратов);

• создавать различные виды графиков и поверхностей.