"Двоичная система счисления"

Двоичная система счисления

Никитина В.Г. учитель информатики высшей категории

Якутской городской национальной гимназии

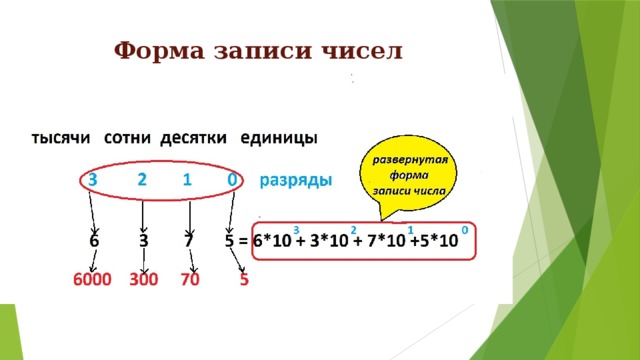
Форма записи чисел

• Чтобы определить число записанное в позиционной системе счисления, нужно значение каждой цифры умножить на основание системы счисления в степени, равной разряду этой цифры, и сложить полученные величины.

• Развернутую запись числа можно использовать для обратного перехода, от десятичной системы к системе с основанием p.

Схема Горнера

• 6375 = ((6 * 10 +3) * 10 +7) * 10 + 5

• • Для вычислений не нужно использовать
• возведение в степень
• • Удобна при вводе чисел с клавиатуры,
• начиная с первой

• Схема Горнера очень удобна для обработки данных при вводе чисел с клавиатуры, когда цифры числа вводятся последовательно, начиная с первой, и их количество заранее неизвестно.

3,2,1,0 а 3 , а 2 , а 1 , а 0 = a 3 * p 3 + a 2 * p 2 * a 1 * p 1 *a 0 * p 0 или с помощью схемы Горнера: а 3 , а 2 , а 1 , а 0 = ((a 3 * p + a 2 ) * p + a 1 ) * p + a 0 Оба способа можно использовать для перевода числа из любой позиционной системы в десятичную систему. Развернутая запись числа можно использовать для обратного перехода, от десятичной системы к системе с основанием p. " width="640"

• Число может быть записано в развернутой форме:
• разряды - 3,2,1,0
• а 3 , а 2 , а 1 , а 0 = a 3 * p 3 + a 2 * p 2 * a 1 * p 1 *a 0 * p 0
• или с помощью схемы Горнера:
• а 3 , а 2 , а 1 , а 0 = ((a 3 * p + a 2 ) * p + a 1 ) * p + a 0
• Оба способа можно использовать для перевода числа из любой
• позиционной системы в десятичную систему.
• Развернутая запись числа можно использовать для обратного перехода, от десятичной системы к системе с основанием p.

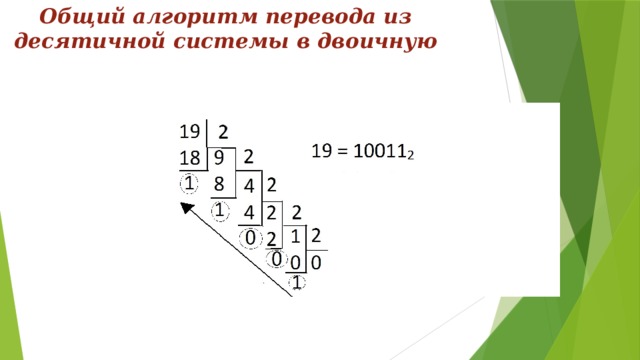
Общий алгоритм перевода из десятичной системы в двоичную

• Для перевода числа из десятичной системы в систему счисления с основанием p, отбрасывая остаток на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке

Определение

• Система счисления – это правила записи чисел с помощью
• специальных знаков – цифр, а также соответствуюшие
• правила выполнения операций с этими числами

Определения ______________________________________

• Позиционная система: значение цифры определяется
• её позицией в записи числа.
• Алфавит системы счисления – зто используемый в
• ней набор цифр.
• Основание системы счисления – это количество цифр
• в алфавите (мощность алфавита).
• Разряд – это позиция цифры в записи числа. Разряды в
• Записи целых чисел нумеруются с нуля справа налево.

Метод подбора

• для перехода чисел из двоичной системы в десятичную, и обратно,
• полезно выучить наизусть таблицу первых десяти степеней двойки:

1

2

2

4

3

4

8

5

16

32

6

7

64

128

8

256

9

512

0

1024

• Переведем число 10101010 из двоичной системы счисления в десятичную.
• Пронумеруем его цифры справа налево, подпишем под ненулевыми разрядами
• соответствующие степени двойки и пронумеруем их:
• 1 0 1 0 1 0 1 0
• 7 6 5 4 3 2 1 0
• 126 32 8 2
• 101010102 = 2 + 8 +32 + 128 = 170

• Для перевода из десятичной в двоичную систему надо разложить данное число
• на степени двойки методом вычитания старшей степени. Например,
• 170 = 128 +42 = 1 * 128 + 0 * 64 + 1 * 32 + 0 * 16 + 1 * 8 +2 =
• 1 * 128 + 0 * 64 +1 * 32 + 0 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 0 * 1
• Выписав двоичные цифры, получаем равенство: 170 10 = 10101010 2

• Обратите внимание, что очень важно довести выписывание степеней до самого конца,
• не потеряв ни одной цифры, так как количество нулей в конце числа имеет большое
• значение!

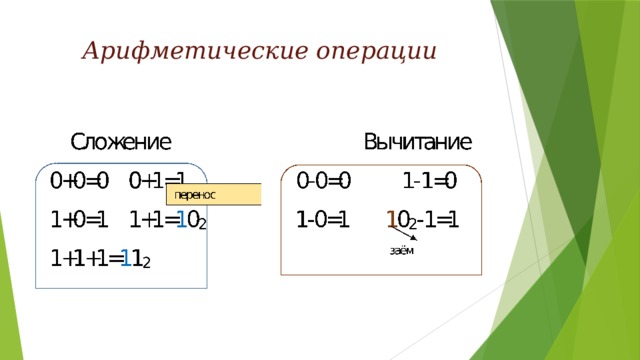
Арифметические операции

Сложение

Вычитание

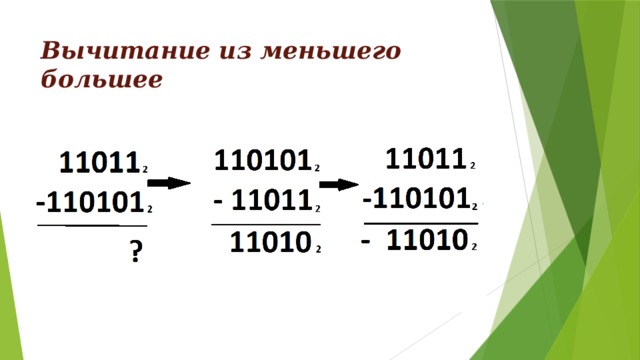
Вычитание из меньшего большее

• Если требуется вычесть большое число из меньшего, вычитают из большего и ставят у результата знак «минус».

Умножение и деление

• Умножение и деление столбиком в двоичной системе выполняются практически так же,
• (но с использованием правил двоичного сложения и вычитания).

Для перехода дробного числа в двоичную систему используется общий подход.

• Для перехода дробного числа в двоичную систему нужно умножить число на 2,
• запомнить целую часть и отбрасывать её перед следующим умножением.

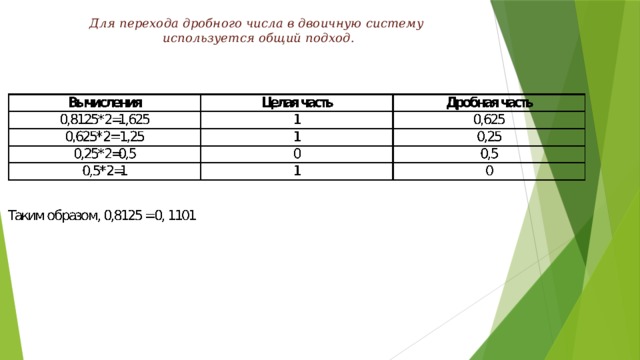
Для перехода дробного числа в двоичную систему используется общий подход.

• Давайте посмотрим, как храниться в памяти число 0,6.
• Выполняя умножение на 2 и выделение целой части,
• мы получим периодическую бесконечную дробь:
• 0,6 = 0, 1001100110012…=0, (1001)2

• Это значит, что для записи десятичного числа 0,6 в двоичной системе счисления требуется бесконечное число разрядов.
• Поскольку реальный компьютер не может иметь бесконечную память, число 0,6 в двоичном представлении храниться с ошибкой (погрешностью).

Определение:

• Большинство дробных чисел храниться в памяти с некоторой погрешностью. При выполнении вычислений с дробными числами погрешности накапливаются и могут существенно влиять на результат.

• Отметим, что эта проблема связана не с двоичной системой, а с ограниченным размером ячейки памяти компьютера, отведенной на хранение числа.

• Если же все-таки нужно обязательно использовать дробные числа и нельзя жертвовать точностью, приходится хранить их в нестандартном виде, например, в виде отношения целых чисел (например, 0,6 = 6/10) и вычислять отдельно числители и
• знаменатели простых дробей, переходя к вещественным числам только при выводе конечного результата.

• Этот подход применяется в системах символьных вычислений, например, программных системах Maple (www.maplesoft.com) и Mathematica (www.wolfram.com).
• Однако выполнение таких расчетов занимает очень много времени.

0,6375 = 6•0,1 + 3•0,01 + 7•0,001 + 5•0,0001 Развёрнутая форма записи:

• разряды: -1 -2 -3 -4
• 0, 6 3 7 5 = 6·10 -1 + 3·10 -2 + 7·10 -3 + 5·10 -4
• 0, 6 3 7 5 = 6·10 -1 + 3·10 -2 + 7·10 -3 + 5·10 -4
• Перевод в десятичную систему
• Схема Горнера:
• 0, 6375 = 10 -1 ·(6 + 10 -1 ·(3 + 10 -1 ·(7 + 10 -1 ·5)))
• 0,1234 5 = 5 -1 ·(1 + 5 -1 ·(2 + 5 -1 ·(3 + 5 -1 ·4)))
•  

Дробные числа: из десятичной в любую

• 0,1234 5 = 5 -1 ·(1 + 5 -1 ·(2 + 5 -1 ·(3 + 5 -1 ·4)))
• 5 ·(0,1234 5 )= 1 + 5 -1 ·(2 + 5 -1 ·(3 + 5 -1 ·4))

Задачи

• Задача : Сколько единиц в двоичной записи числа 64?
• 64 = 1*64 + 0*32 + 0*16 + 0*8 + 0*4 +0*2 + 0*1;
• 64 = 1000000 2 ; Ответ: 1;

• Задача : В системе счисления с некоторым основанием число 12 n
• записывается 110. Укажите это основание.
• Обозначим искомое основание n.
• I вариант: 110 n = n 2 + n 1 + 0; n 2 + n = 12;
• Решая квадратное уравнение, находим два корня:
• n 1 = 3 и n 2 = - 4 ( не подходит)
• Получаем: 9 + 3 + 0 = 12;

• II вариант: 110 n = n 2 + n 1 + 0;
• При n = 2; 4 + 2 = 6; 110 2 = 6 10 ;
• При n = 3; 110 3 = 3 2 + 3 + 0 = 12 10 ;
• Ответ: 3

5 переводим правую часть в десятичную систему в записи есть цифра 5, поэтому X 5 переводим правую часть в десятичную систему 210 155 х =1* Х 2 + 5*Х 1 + 5* Х 0 = Х + 5* Х + 5 решаем уравнение: 71 = X 2 + 5·X + 5 Х = 6; Х = - 11( не подходит ) " width="640"

• Задача: в некоторой системе счисления число 71 записывается как «155 x »? Определите основание системы счисления X .
• 71 = 155 X
•  

• в записи есть цифра 5, поэтому X 5 переводим правую часть в десятичную систему
• в записи есть цифра 5, поэтому X 5
• переводим правую часть в десятичную систему
• 210
• 155 х =1* Х 2 + 5*Х 1 + 5* Х 0
• = Х + 5* Х + 5

• решаем уравнение:
• 71 = X 2 + 5·X + 5
• Х = 6;
• Х = - 11( не подходит )

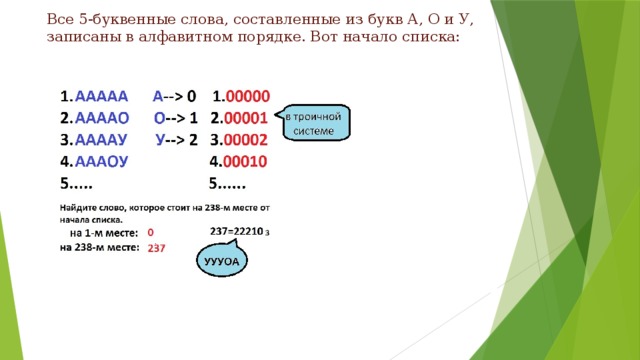
Все 5-буквенные слова, составленные из букв А, О и У, записаны в алфавитном порядке. Вот начало списка:

Решение:

• 238 -?
• А =0, О =1, У =2;
• 3 5 =243;
• 238 (3 4 =81; 3 3 =27; 3 2 =9; 3 1 =3; 3 0 =1;)
• 237=2*81+2*27+2*9+1*3+0*1=22210 3
• Ответ: УУУОА

Выводы

• Двоичная система счисления служит основой всех расчетов в современных компьютерах.

Она обладает следующими преимуществами:

• • Для того, чтобы построить компьютер, работающий с двоичными данными, достаточно иметь устройства с двумя состояниями
• (включено/выключено); первыми такими устройствами были электромагнитные реле, сейчас применяются микроэлектронные элементы;
• • Надежность и защита от помех при передаче информации
• (для приёма двоичного кода не нужно точно измерять сигнал, достаточно знать, какое из двух значений он принимает в каждый заданный момент времени);
• • Компьютеру проще выполнить вычисления с двоичными числами, нежели с десятичными; например, умножение фактически сводится к многократному сложению,
• а деление – к вычитанию.

Тем не менее, с точки зрения человека у двоичной системы есть недостатки;

• двоичная запись чисел получается длинная: например, число 1024 записывается
• в виде 10000000000 2 – здесь легко перепутать количество идущих подряд нулей;
• запись однородна, т.к. содержит только нули и единицы; поэтому при работе с двоичными числами легко ошибиться или запутаться.

• Спасибо за внимание!