Муниципальное общеобразовательное автономное учреждение
«Основная общеобразовательная школа №55» г. Оренбург
Направление статьи: Математика
Тема: Числа Фибоначчи в исторических периодах древнейшей
и современной истории
Автор работы:
Верейкина Т.В.
учитель математики
Кайда Е.Е., учитель математики
2023
Оглавление
Введение……………………………………………………………………………………… 3 Глава 1. Числа Фибоначчи и золотое сечение...……………………………………………………………………………………… 4 Глава 2. Исследования ученых...…………………………………………………………. 5 Глава 3. Связь между историческими периодами и числами Фибоначчи…………. 6 Заключение………………………………………………………………………………….. 8 Библиографический список……………………………………………………………….. 9
2
Введение
Развитие человечества разграничивается определенными периодами в древнейшей и современной истории. Могут ли элементы ряда чисел Фибоначчи соответствовать хронологическим рубежам периодов в древнейшей и современной истории человечества, т. е. подчиняются ли рубежи периодов математической закономерности? Существует ли такая закономерность в других периодах: периодах мировой истории, периодах правления известных Российских государственных деятелей, и в датах современных событий, имеющих историческое значение? Цель нашей работы заключается в проведении аналогии между математикой и историей, то есть установлении некоторой связи. Для достижения данной цели необходимо было решить следующие задачи:
-
Познакомиться с числами Фибоначчи и золотым сечением, которое является самым гармоничным отношением;
-
Проверить, соответствуют ли рубежи периодов древнейшей, современной и мировой истории числам ряда Фибоначчи;
-
Рассчитать годы правления известных Российских государственных деятелей и найти их отношение;
-
Рассмотреть даты, имеющие историческое значение, во временных промежутках современной истории;
-
Проверить, являются ли полученные отношения между данными объектами известными математическими отношениями.
Объектами исследования будут являться археологические эпохи, периоды мировой истории, периоды правления известных Российских государственных деятелей, даты событий, имеющие историческое значение. Весьма полезными для нас оказались результаты исследований социолога – аналитика В. В. Дудихина, и метод поэта и переводчика А. Чернова, которые подтверждают математические закономерности чисел Фибоначчи, соответствующие хронологическим рубежам древнейшей истории человечества. Работа относится к прикладным исследованиям, ее результаты, выраженные с помощью математики, покажут связь между математикой и историей, которая подчиняется математическим законам.
3
Глава 1. Числа Фибоначчи и золотое сечение
Числовая последовательность, в которой, сумма двух соседних чисел дает значение следующего за ними является последовательностью Фибоначчи (например, 1+1=2; 2+3=5 (1,1,2,3,5,8,13,21,34,55 и т.д.)). Свойства различных членов последовательности, так называемые коэффициенты Фибоначчи, (т.е. постоянные отношения) определяются следующим образом:
-
Отношение каждого числа к последующему более и более стремится к 0,618 по увеличению порядкового номера. Отношение же каждого числа к предыдущему стремится к 1,618 (обратному к 0,618);
-
При делении каждого числа на следующее за ним через одно получаем число 0,382, наоборот – соответственно 2,618;
-
Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4,235; 2,618; 1,618; 0,618; 0,382; 0,236; упомянем также 0,5. Все они играют особую роль в природе, и в частности – техническом анализе.
Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи.
Обратимся к числу 0,618, мы уже его встречали (коэффициент Фибоначчи). Это числовое значение золотого сечения.
Одна из пропорций чаще других встречающаяся в искусстве получила название «золотое сечение» - деление отрезка, при котором одна его часть во столько же раз больше другой, во сколько сама она меньше целой. Пропорциональные отношения, близкие к золотому сечению дают впечатление развитие форм, их динамики, пропорционального дополнения друг друга.
4
Глава 2. Исследования ученых
Обратимся к современным исследованиям: социолога – аналитика В.В. Дудихина, поэта и переводчика А. Чернова.
Социолог и аналитик В.В. Дудихин рассмотрел хронологию эпох, в качестве инструмента хронологии он избрал гармоническую систему числовых отношений, так называемый ряд Фибоначчи. В.В. Дудихин сопоставил числа ряда Фибоначчи и археологические эпохи. Его исследования показали, что некоторые элементы этой последовательности, действительно, соответствуют хронологическим рубежам в древнейшей истории человечества, особенно если к числам добавить наименование "тыс. лет до н. э.", или "тыс. лет тому назад", или просто "тыс. лет". Хронология и периодизация исторического развития с помощью ряда Фибоначчи разделена на 18 временных ступеней: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1 597, 2 584, что подтверждается 60% проверенных совпадений.[5]
Так же, полезным нам окажется метод А.Чернова, в основу которого положено нахождение отношений частей одного целого, т.е. пропорциональные отношения.
Внимание Чернова привлекли рассуждения о золотом сечении и числе π, которые восходят к Пифагору. Исследования Андрей Чернова позволили сделать заключение о том, что построение стихов древнего автора «Слова о полку Игореве», состоящего из девяти песен, подчиняется математическим законам. А именно, если число стихов во всех трех частях (их 804) разделить на число стихов в первой и последней части (256), получается 3,14, т.е. число π с точностью до третьего знака.[7]
Вышеназванные исследования, представляют интерес, не только, в плане используемых методов, но и в плане полученных результатов. Опираясь на данные современных исследований можно предположить, что не только эти археологические эпохи, но и другие исторические периоды подчиняются математическим законам.
5
Глава 3. Связь между историческими периодами и законами математики
Проведем аналогию между рубежами исторических периодов, числами Фибоначчи и золотым сечением, основываясь на данные ученых и собственные исследования. Для этого рассмотрим некоторые рубежи исторических периодов, в хронологии с древнейшей и современной историей.
-
Проверим исследование социолога В.В. Дудихина рубежей исторических периодов в хронологии c древнейшей историей. Сопоставим рубежи исторических периодов с числами Фибоначчи, т.е. проведем их соответствие. Для этого рассмотрим рубежи периодов древнейшей истории:
Железный век датируется II тыс. н.э.. На Ближнем Востоке, Египте, Греции – с начала I тыс. н.э., в Африке – с I тыс. н.э.;
Бронзовый век датируется в Южной Америке с середины I тыс. н.э., в Тропической Африке с I тыс. н.э., в Европе с середины III тыс. до н.э., в Индии с конца III тыс. до н.э., в Египте с начала II тыс. до н.э., в Передней Азии с конца IV тыс. до н.э.;
Медный век (энеолит) датируется VIII – IV тыс. до н.э.;
Каменный век (палеолит) ранний датируется до 35 тыс. лет назад, поздний 35 – 13 тыс. лет назад;
Каменный век (мезолит) датируется с начала XX – VIII тыс.до н.э. поV – IV тыс. н.э.;
Каменный век (неолит) датируется VIII – III тыс. н.э.;
Если рассмотреть происхождение человека, то выделяют следующие рубежи периодов: Australopithecus anfmensis, 4 - 3,7 млн. лет назад, Australopithecus africanus, 3-2 млн. лет, Australopithecus boisei, 2,4 - 1,1 млн. лет, Homo rudolfensis, 2,5 – 1,8 млн. лет, Homo erectus, 1,8 – 400 тыс. лет, Homo neandertalensis, 220 – 27 тыс. лет Полученные результаты соответствуют числам Фибоначчи (1, 3, 8, 13, 21, 33, 233, 1597, 2584, 4181) или близки к ним (приложение № 1).
-
Проведем исследование рубежей периодов мировой истории и предистории: Эпоха первобытно общинных отношений 2,5 мил. лет назад - III тыс. до н.э.; Древний мир III тыс. до н.э.- V тыс. н.э.; История средних веков V века - конец XV века; История нового времени XVI – XX в.; Современная эпоха XX – XXI в. Полученные результаты соответствуют числам Фибоначчи (3, 5, 13, 21) или близки к ним.
-
Проведем исследование периодов правления известных Российских государственных деятелей с 862 г. н.э.
6
Пересчитаем годы их правления:
Рюрик (862 – 879) – 17 лет; Василий III (1505 – 1533) – 28 лет; Иван Грозный (1533 - 1584) – 51 год; Романов М.Ф. (1613 – 1676) – 63 года; Пётр I (1682 – 1725) – 43 года; Екатерина II (1762 – 1796) – 34 года; Александр II (1855 – 1981) – 26 лет; Николай II (1894 – 1917); падение монархии Романовых 1917 до 1931 – 14 лет; Сталин И.В. (1931 -1953) – 22 года; Хрущев Н.С. (1953 – 1964) – 11 лет; Брежнев Л.И. (1964 – 1982) – 18 лет; Горбачев М.С. (1985 – 1991) – 6 лет; Ельцин Б.Н. (1991 – 1999) – 8 лет; Путин В.В. (2000 – 2008) – 8 лет.
Найдем отношения годов правления.
Если разделить годы правления Рюрика (17 лет) на годы правления Василия III (28 лет), то их отношение равно 0,607. Если разделить годы правления Василия III (28 лет) на годы правления Ивана Грозного (51 год), то их отношение равно 0,549. Если разделить годы правления Ивана Грозного (51 год) на сумму годов правления Василия III и Ивана Грозного (79 лет), то их отношение равно 0,646. Отношение годов правления Романова М.Ф. (63 года) к годам правления Петра I (43 года) равно 0,682. Отношение годов правления Екатерины II (34 года) к годам правления Романова М.Ф. (63 года) равно 0,54. Если разделить годы правления Петра I (43 года) на сумму годов правления Петра I и Екатерины II (77 лет), то их отношение равно 0,55. Отношение годов правления Сталина И.В. (22 года) к сумме годов от 1917 до 1953 (36 лет) равно 0,611 т.е. числовое значение золотого сечения с точностью до третьего знака;
Отношение годов правления Хрущева Н.С. (11 лет) к сумме годов от 1917 до 1964 (47 лет) равно 0,234. Отношения годов правления Хрущева Н.С. (11 лет) к годам правления Брежнева Л.И. (18 лет) и наоборот, равны соответственно 0,611 и 1,636. Данные отношения близки к фибоначчиевским коэффициентам (0,236; 0,618; 1,618) с точностью до третьего и второго знаков соответственно. Отношение годов правления Сталина И.В. (22 года) к сумме годов правления Сталина И.В. и Хрущева Н.С. (33 года) равно 0,666. Отношение годов правления Горбачёва М.С. (6 лет) к годам правления Хрущева Н.С. (11 лет) равно 0,545. Отношения годов правления Хрущева Н.С. (11 лет) к сумме годов правления Хрущева Н.С. и Брежнева Л.И. (29 лет) и наоборот, равно соответственно 0,379 и 0,620 т.е. фибоначчиевским коэффициентам (0,382; 0,618) с точностью до второго знака.
7
-
Рассмотрим временные промежутки, периоды правления известных Российских государственных деятелей, и даты некоторых событий в эти периоды, имеющие историческое значение.
-
Временной промежуток с 1984 по 1917 год, годы правления Николая II. Историческим событием является 1904 год – начало Русско-японской войны. Найдем отношение годов после данного события (13 лет), во временном промежутке, к годам всего временного промежутка (23 года). Отношение годов равно 0,565.
-
Временной промежуток с 1894 по 1931 год, с начала правления Николая II по начало правления Сталина И.В. Историческим событием является 1917 год – начало революции в России. Найдем отношение годов до данного события (23 года) к годам после данного события (14 лет). Отношение годов равно 1,64.
-
Временной промежуток с 1917 по 1931 год, падение монархии Романовых. Историческим событием является 1922 год - образование Союза Советских Социалистических республик. Найдем отношение годов до данного события (5 лет) к годам после данного события (9 лет). Отношение годов равно 0,556.
-
Временной промежуток с 1931 по 1953 год, годы правления Сталина И. В. Историческим событием является 1941 год – нападение Германии на СССР, Найдем отношение годов до данного события (10 лет) к годам данного временного промежутка (22 года). Отношение годов равно 0,454.
-
Временной промежуток с 1985 по 2000 год, с начала правления Горбачева М.С. по начало правления Путина В.В. Историческим событием является 1991 год – распад Союза Советских Социалистических республик. Найдем отношение годов до данного события (6 лет) к годам после данного события (9 лет). Отношение годов равно 0,666.
Полученные результаты соответствуют фибоначчиевским коэффициентам
(0,618; 1,618) с точностью до второго знака или близки к ним (приложение № 2).
8
Заключение
В результате изучения различных источников и проведенного нами самостоятельного исследования, можно сделать выводы:
-
Подтвердилось исследование социолога Дудихина В.В. о том, что рубежи периодов древнейшей истории соответствуют числам Фибоначчи или близки к ним (1, 3, 8, 13, 21, 34, 144, 233, 1 597, 2 584, 4181);
-
Рубежи периодов мировой истории и предистории так же соответствуют числам Фибоначчи (3, 5, 13, 21) или близки к ним;
-
Отношения годов правления известных Российских государственных деятелей соответствуют как числовому значению золотого сечения с точностью до второго и третьего знаков соответственно (0,6; 0,611), так и фибоначчиевским коэффициентам (0,234; 1,636; 0,379 и 0,620) с точностью до третьего и второго знаков соответственно;
-
Рассмотренные даты, во временных промежутках, являются «точками золотого сечения», т. е. делят временные промежутки на пропорциональные отрезки соответствующие фибоначчиевским коэффициентам (0,666; 1,64) с точностью до второго знака.
Таким образом, подтверждается связь между математикой и историей. И это не случайно, ведь каждой области присуще стремление к соразмерности и гармонии, независимо от того, история это или математика.
9
Библиографический список
-
Брей У., Трамп Д. Археологический словарь. - М., 1990.
-
Всемирная история Энциклопедия этнографии и археологии. – М.: Дрофа, 2003.
-
Данилов А.А., Косулина Л.Г. История России XIX – начало XXI века. – М: Просвещение, 2003.
-
Данилов Д.Д., Кузнецов А.В. История России 5-9 класс. – М.: Баласс, 2008.
-
Дудихин В.В. Новейшая история России XX–XXI в. и последовательность Фибоначчи.- www.vaal.ru/show.php?id=156
-
Зубов А. Происхождение человека. – Журнал «Вокруг света» №5, 2003.
-
Словарь иностранных слов. – М.: «Русский язык», 1990.
-
Чепракова Е.И., Липкина Т.А. Присутствие красоты. – Журнал «Математика в школе» №3, 2001.
-
Ятайкина А.А. О золотом сечении и не только о нем. - Журнал «Математика в школе» №3, 2001.
10
Приложение № 1
Составим таблицу рубежей исторических периодов, приняв за единицу счета времени 1 000 лет, и сравним их с числами последовательности Фибоначчи:
| Числа последовательности Фибоначчи | Временные даты | Исторические периоды |
| 4181 | 4000 | Australopithecus anamensis |
| 2584 | 2500 | Homo rudolfensis |
| 1597 | 1800 | Homo erectus |
| 233 | 220 | Homo neandertalensis |
| 34 | 35 | Каменный век (палеолит) ранний |
| 21 | 20 | Каменный век (палеолит) средний |
| 13 | 13 | Каменный век (палеолит) поздний |
| 3, 8 | 3 | Каменный век (неолит) |
| 8 | 8 | Медный век (энеолит) |
| 1, 3 | 1, 3 | Бронзовый век |
| 1 | 1 | Железный век |
11
Приложение № 2
Временные промежутки:
-
с 1894 по 1931 год. Отношение годов 23 : 14 равно 1,64

-
с 1917 по 1931 год. Отношение годов 5 : 9 равно 0,556.

-
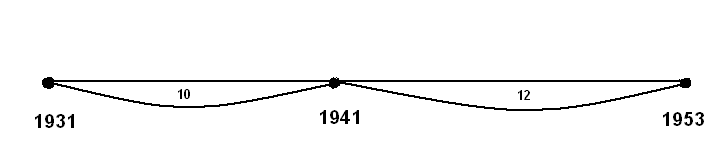
с 1931 по 1953 год. Отношение годов 10 : (10 + 12) равно 0,454.
-
с 1985 по 2000 год. Отношение годов 6 : 9 равно 0,666.

12

 Получите свидетельство
Получите свидетельство Вход
Вход












 Числа Фибоначчи в исторических периодах древнейшей и современной истории (57.76 KB)
Числа Фибоначчи в исторических периодах древнейшей и современной истории (57.76 KB)
 0
0 310
310 1
1 Нравится
0
Нравится
0


