Анимированная презентация «Обратные тригонометрические функции»

Определение арксинуса,

арккосинуса, арктангенса и арккотангенса

числа а

Арксинус числа а , |а | ≤ 1 есть такое число α из промежутка [– π / 2; π / 2 ], синус которого равен числу а

Sin

π /2

arc sin ( – a ) = – arc sin a

1

arc sin a

а

α

– α

x

– a

-1

arc sin ( – a )

- π /2

Sin

π /2

Вычислите :

- π /2

Ищу число из отрезка

[ - π /2; π /2] , синус которого равен …

Арккосинус числа а , |а | ≤ 1 есть такое число α из промежутка [ 0; π ], косинус которого равен а

Sin

arc cos ( – a ) = π – arc cos a

arc cos a

arc со s ( – a )

α

0

π

Cos

-1

1

– a

а

Вычислите :

Cos

π

0

Ищу число из отрезка [0; π ] , косинус которого равен…..

Имеет ли смысл выражение?

а rcsin (-1/2) arccos arcsin

да нет нет

а rcsin 1,5 arccos arccos

нет да да

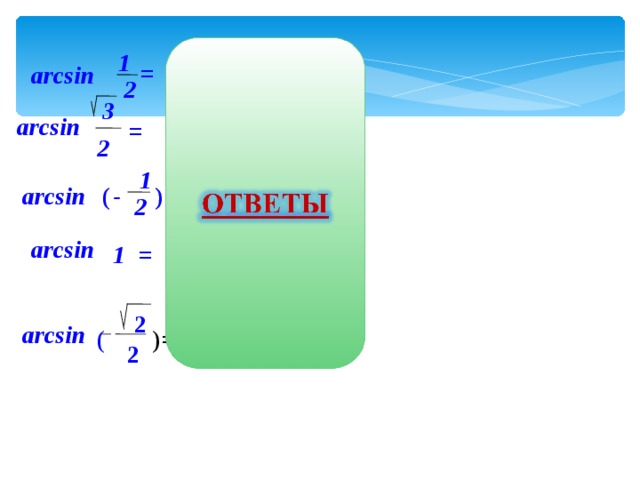
π

1

=

arcsin

6

2

3

π

3

arcsin

=

2

π

1

-

)

(

arcsin

-

6

=

2

π

arcsin

1 =

2

π

2

arcsin

-

=

(

)

4

2

7

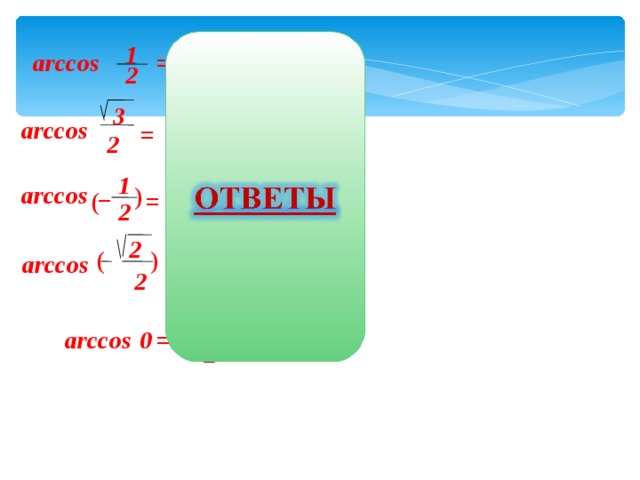
π

1

3

arccos

=

2

π

3

arccos

=

2

6

2 π

1

1

arccos

)

arccos

π ̶

=

−

=

(

2

2

3

2

3 π

)

(

arccos

=

2

4

π

0

=

arccos

2

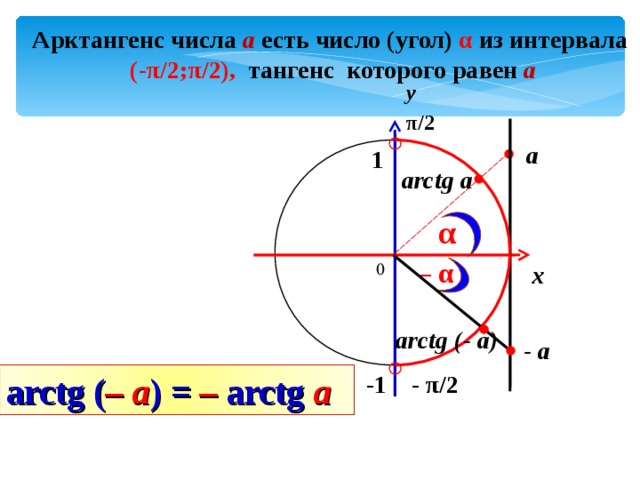
Арктангенс числа а есть число (угол) α из интервала

(- π /2; π /2), тангенс которого равен а

у

π /2

○

а

1

arctg a

α

– α

х

0

arctg (- a )

- а

○

- π /2

arctg ( – a ) = – arctg a

-1

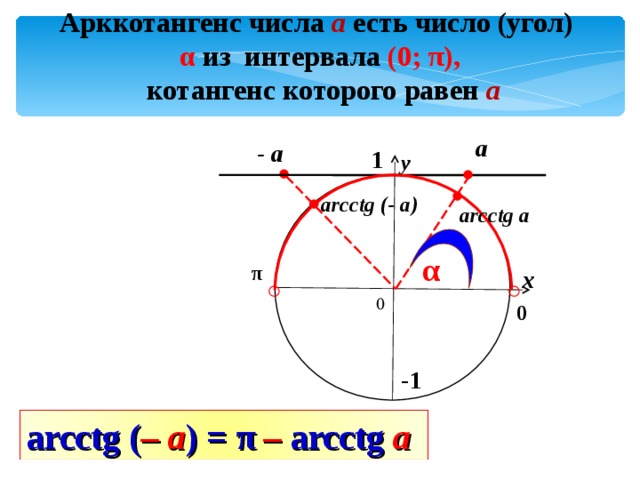
Арккотангенс числа а есть число (угол)

α из интервала (0; π ),

котангенс которого равен а

а

- а

1

у

arcctg (- a)

arcctg a

α

π

х

○

○

0

0

-1

arcctg ( – a ) = π – arcctg a

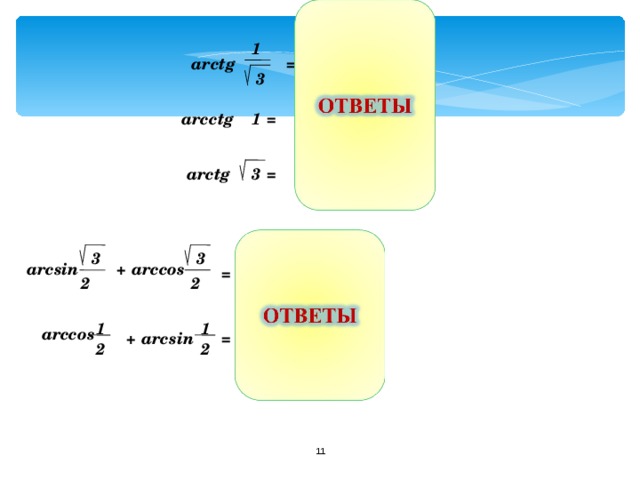
П

1

=

ar с tg

6

3

П

ar с ctg

1

=

4

П

3

3

ar с tg

=

3

3

П

П

П

3

arccos

arcsin

+

+

=

=

6

2

2

2

1

1

П

arccos

П

П

+

=

3

+

=

arcsin

2

6

2

2

11