Аксиомы параллельных прямых

Предмет: геометрия (7 класс) Тема: Аксиома параллельных прямых

Подготовила материал: Учитель по математике, МБОУ СШ № 30 города Дзержинск: Кобякова Анна Викторовна

Введение: Аксиома параллельных прямых

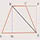
• Рассмотрим произвольную прямую и точку М, не лежащую на ней (Рис.1).
• Докажем, что через точку М можно провести прямую, параллельную прямой . Для этого проведем через точку М две прямые: сначала прямую перпендикулярно к прямой , а затем прямую перпендикулярно к прямой (Рис.2). А из того, что две прямые и перпендикулярны к третьей прямой следует, что они параллельны (а||b).

Введение: Аксиома параллельных прямых

• Возникает вопрос: можно ли через точку М провести еще одну прямую, параллельную прямой ?

• Если прямую "повернуть" на какой-то угол вокруг точки М, то она пересечет прямую (прямая ' на рис.3).

• То есть нам кажется, что через точку М нельзя провести прямую отличную от прямой , параллельную прямой . Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой.

Введение: Аксиома параллельных прямых

• Таким образом мы можем сделать следующий вывод:
• Через точку не лежащую на прямой проходит одна прямая, параллельная данной .

Аксиома параллельных прямых (следствия )

• 1). Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую . Данное свойство можно доказать на следующем примере:
• Дано: a||b, c ∩ a = М(Рис.4).
• Доказать: c ∩ b

Аксиома параллельных прямых (следствия )

Доказательство :

Если мы предположим, что прямая не пересекает прямую , то прямая будет параллельна прямой , а по условию через точку М проходит прямая параллельная прямой , значит получим, что через точку М будут проходить две прямые и параллельные прямой (Рис.5).Но это противоречит аксиоме параллельных прямых, значит, наше предположение неверно, и прямая пересекает прямую , т.е. . Что и требовалось доказать.

Аксиома параллельных прямых (следствия )

• 2). Если две прямые параллельны третьей прямой, то они параллельны. Данное свойство мы докажем следующим образом.
• Дано: a || c, b||c (Рис.6)
• Доказать : а||b

Аксиома параллельных прямых (следствия )

• Доказательство:
• Предположим, что прямые и не параллельны, т.е. пересекаются в некоторой точке М (Рис.7).Тогда получим, что через точку М проходят две прямые и параллельные прямой , т.к. по условию и . Но это противоречит аксиоме параллельных прямых, следовательно, наше предположение неверно, значит, прямые и параллельны, т.е. . Что и требовалось доказать.

• Следствие - утверждение, которое выводится непосредственно из аксиом или теорем.

Аксиома параллельных прямых (задачи)

Ссылки:

• Учебник А.Атанасян « Геометрия 7-8-9 класс» стр. 57-60, стр.65
• https:// budu5.com/manual/chapter/3400
• http://ru.solverbook.com/spravochnik/aksiomy/aksioma-parallelnyx-pryamyx /