Приложение
к основной образовательной программе
приказ № _____ от _______ 2016года
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №18
имени Виталия Яковлевича Алексеева г. Сургута
Адаптированная рабочая программа
для глухих детей
по алгебре и началам анализа
на 2016- 2017 учебный год
класс 10(11)Г
учитель: Гусева Светлана Геннадьевна
| Количество часов по учебному плану | 4 | ||
| Всего за учебный год | 140 | ||
|
В т.ч. | 1 –я четверть | 34 | |
| 2 –я четверть | 30 | ||
| 3 – я четверть | 38 | ||
| 4 – я четверть | 38 | ||
Планирование составлено на основе программы (указать автора, год издания, кем рекомендована)
Т.А. Бурмистрова. Программы общеобразовательных учреждений. Алгебра 10-11 классы. М., “Просвещение” 2009г
Учебник (указать автора, год издания, кем рекомендован)
Ш.А. Алимов. Алгебра. Учебник для 10-11 класса общеобразовательных учреждений. М.,”Просвещение”, 2016 г., рекомендовано Министерством образования РФ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по алгебре для 10 класса составлена в соответствии с требованиями федерального компонента государственного образовательного стандарта основного общего образования по математике, с учётом примерной программы «Программы общеобразовательных учреждений»; составитель Т.А.Бурмистрова; Издательство «Просвещение» 2009г., федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2016-17 учебный год,.
Рабочая программа составлена для обучения глухих учащихся 10(11)Г класса и строится на основе программы общеобразовательных учреждений для 10 класса (ниже на один год).
В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося и выпускника, виды контроля, а также компьютерное обеспечение урока.
Основным способом восприятия учебного материала на уроках математики является слухо-зрительный, но, как и на других уроках, производится работа по развитию остаточного слуха школьников. В материал каждого урока включаются задания, воспринимаемые только на слух. К таким заданиям относятся поручения, организующие урок типа: «Открой (-те) учебники на странице…», «Запиши (-те) домашнее задание» и др.; знакомые формулировки инструкций; вопросы по пройденному материалу. Работа по развитию способов восприятия речи детьми на уроках математики ведется в соответствии с основными сурдопедагогическими требованиями к этому процессу на фронтальных занятиях.
Процесс обучения нужно строить так, чтобы привить детям умения и навыки, необходимые для самостоятельного решения новых вопросов, новых учебных задач. Поэтому в каждой теме необходимо предусмотреть выполнение самостоятельных работ, имеющих различные дидактические цели. Для составления текстов самостоятельных и контрольных работ учитель может использовать задачи и упражнения, предложенные в программе по каждой теме.
Учитывая объем и характер учебного материала, которым должны овладеть школьники, необходимо следить за тем, чтобы дети не были перегружены учебным материалом как на уроках, так и во время выполнения домашних заданий. На уроках нужно заботиться о рациональной смене видов деятельности, способствующих разрядке и снижающих утомление.
При изучении курса алгебры и геометрии в 11 В классе большой упор необходимо делать на активизацию речевого словаря. Содержание математического обучения учащихся с проблемами слуха должно строиться с учетом развития и формирования психических процессов неслышащих школьников, их познавательной активности.
На всем протяжении обучения сохраняется коррекционная направленность обучения, которая позволяет усвоить глухому ученику требуемый объем знаний, подняться до уровня развития, необходимого для интеграции в обществе. Комплексное воздействие на нарушение функции в специально организованном процессе обучения помогает сгладить основной дефект глухого и приблизить его к естественному пути развития. Необходимо использовать различную наглядность на уроках, которая способствует развитию воображения и более длительному сохранению в памяти учебного материала, стимулирует познавательный интерес к изучаемому предмету. Особое значение в обучении неслышащих придается соотношению между словом учителя и наглядностью. Накопление речевого словаря и развитие произношения должно прослеживаться на всех уроках в единой системе.
В программах школы для глухих определяются объем и характер речевого материала, подлежащего усвоению глухими учащимися в процессе изучения любого общеобразовательного курса
Изучение математики в старшей школе на базовом уровне направлено на достижение следующей цели:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
систематизировать сведения о числах; изучить новые виды числовых выражений и формул; совершенствовать практические навыки, расширить и совершенствовать алгебраический аппарат, сформированный в основной школе, и его применение к решению математических и нематематических задач;
расширить и систематизировать общие сведения о функциях, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
- развить представление о вероятностно-статистических закономерностях в окружающем мире, совершенствовать интеллектуальные и речевые умения путем обогащения математического языка, развивать логическое мышление;
знакомить с основными идеями и методами математического анализа.
Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются разные виды самостоятельных работ: двухуровневая – уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5»; большой список заданий разного уровня, из которого учащийся решает их по своему выбору. Рядом с учеником на таких уроках – включенный компьютер, который он использует по своему усмотрению.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Применение анимации при создании такого компьютерного продукта позволяет рассматривать вопросы математической теории в движении, обеспечивает другой подход к изучению нового материала, вызывает повышенное внимание и интерес у учащихся.
Изучение многих тем в математике связано со знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Тренировочные упражнения.
Включают в себя задания с вопросами и наглядными ответами, составленными с помощью анимации. Они позволяют ученику самостоятельно отрабатывать различные вопросы математической теории и практики.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану на изучение алгебры и начала анализа в 10 классах отводится не менее 105 часов из расчета 3 ч в неделю, из школьного компонента выделяется еще 1 час в неделю, итого 4 недельных часа или 140 часов за год.
В соответствии с учебным планом школы изменено календарно-тематическое планирование. Добавленные часы школьного компонента используются для более полной реализации поставленных целей изучения математики в 10 классе: при проведении повторения в начале учебного года, без которого невозможно успешное усвоение нового материала; для организации тематического контроля; для изучения важных тем: «Тригонометрические уравнения», «Тригонометрические формулы», «Степенная функция» и др.
| ТЕМЫ | Часы из школьного компонента |
| Повторение курса 9 класса | 5 |
| Действительные числа | 3 |
| Степенная функция | 4 |
| Показательная функция | 2 |
| Логарифмическая функция | 3 |
| Алгебраические уравнения. Системы нелинейных уравнений | 3 |
| Тригонометрические формулы | 4 |
| Тригонометрические уравнения | 4 |
| Повторение | 7 |
| Итого: | 35 |
ОСНОВНОЕ СОДЕРЖАНИЕ
| АЛГЕБРА |
| Корни и степени. Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования. Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений. Простейшие тригонометрические уравнения и неравенства. Арксинус, арккосинус, арктангенс числа. |
| ФУНКЦИИ |
| Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция. Область определения и область значений обратной функции. График обратной функции. Степенная функция с натуральным показателем, её свойства и график. Тригонометрические функции, их свойства и графики; периодичность, основной период. Показательная функция (экспонента), её свойства и график. Логарифмическая функция, её свойства и график. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой , растяжение и сжатие вдоль осей координат. |
| НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА |
| Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Понятие о непрерывности функции. Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной. Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл. |
| УРАВНЕНИЯ И НЕРАВЕНСТВА |
| Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных и тригонометрических уравнений. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений. |
| ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ |
| Табличное и графическое представление данных. Числовые характеристики рядов данных. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов. |
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
| В результате изучения математики на базовом уровне ученик должен: знать/понимать
| |
| АЛГЕБРА | уметь:
|
| ФУНКЦИИ И ГРАФИКИ | уметь:
|
| НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА | уметь:
|
| УРАВНЕНИЯ И НЕРАВЕНСТВА | уметь:
|
| ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ | уметь:
|
ОСНОВНАЯ ЧАСТЬ
Тема 1. «Повторение курса алгебры основной школы»(5 часов)
Раздел математики. Сквозная линия
· Числа и вычисления
· Вычисления и преобразования
· Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
· Действия с обыкновенными и десятичными дробями.
· Положительные и отрицательные числа.
· Модуль числа.
· Квадратный корень.
· Разложение многочленов на множители.
· Алгебраические дроби.
· Свойства степени с целым показателем.
· Уравнение с одной переменной.
· Квадратное уравнение.
· Рациональное уравнение.
· Системы уравнений.
· Неравенства.
Требования к математической подготовке
Уровень возможной подготовки обучающегося
· Уметь выполнять арифметические действия с рациональными числами, сравнивать их.
· Уметь выполнять действия со степенями с натуральным и целым показателями, многочленами, алгебраическими дробями.
· Уметь решать линейные, квадратные, простейшие рациональные уравнения, системы уравнений, линейные неравенства, неравенства второй степени.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника
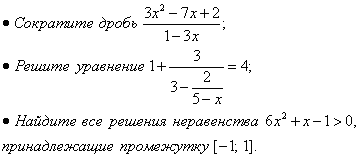
Тема 2. Тема «Действительные числа» (14 часов)
Раздел математики. Сквозная линия
· Числа и вычисления
· Вычисления и преобразования
Обязательный минимум содержания образовательной области математика
· Действительные числа.
· Свойства арифметических действий с действительными числами.
· Сравнение действительных чисел.
· Бесконечно-убывающая геометрическая прогрессия.
· Обращение периодической десятичной дроби в обыкновенную.
· Арифметический корень натуральной степени.
· Свойства арифметического корня натуральной степени.
· Преобразование выражений, содержащих арифметический корень.
· Степень с рациональным и действительным показателем.
· Свойства степени.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Иметь представление о расширении множества чисел, свойствах чисел.
· Уметь выполнять арифметические действия с действительными числами.
· Иметь представление об обращении периодической десятичной дроби в обыкновенную с помощью бесконечно-убывающей геометрической прогрессии.
· Знать свойства арифметического корня натуральной степени.
· Уметь выполнять простые преобразования выражений, содержащих арифметический корень .
· Знать определение степени с рациональным и действительным показателем.
· Уметь вычислять степень с рациональным и действительным показателем
Уровень возможной подготовки обучающегося
· Иметь представление о расширении множества чисел.
· Знать свойства чисел и уметь применять их при выполнении арифметических действий с действительными числами.
· Уметь выполнять обращение периодической десятичной дроби в обыкновенную с помощью бесконечно-убывающей геометрической прогрессии.
· Иметь представление о пределе последовательности.
· Знать свойства арифметического корня натуральной степени.
· Уметь выполнять преобразования выражений, содержащих арифметический корень .
· Знать определение степени с рациональным и действительным показателем.
· Уметь вычислять степень с рациональным и действительным показателем..
· Уметь выполнять преобразования выражений, применяя свойства степеней
Уровень обязательной подготовки выпускника
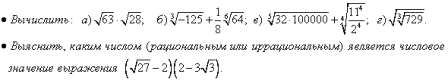
Уровень возможной подготовки выпускника
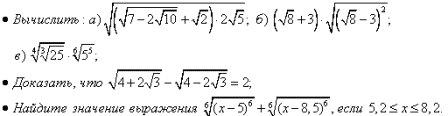
Тема 3. «Степенная функция» (14 часов)
Раздел математики. Сквозная линия
· Функции
· Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
· Степенная функция.
· Свойства степенной функции.
· График степенной функции.
· Равносильные уравнения и неравенства.
· Иррациональные уравнения.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Иметь наглядное представления об основных свойствах функций.
· Изображать графики степенной функции.
· Описывать свойства этих функций, опираясь на график.
· Уметь решать иррациональные уравнения и неравенства, используя стандартный алгоритм их решения.
Уровень возможной подготовки обучающегося
· Иметь наглядное представления об основных свойствах функций, иллюстрировать их с помощью графических изображений.
· Изображать графики степенной функции. Описывать свойства этих функций, опираясь на график.
· Уметь использовать свойства функции для сравнения и оценки ее значений.
· Уметь решать иррациональные уравнения и неравенства, применяя различные методы их решения.
Уровень обязательной подготовки выпускника
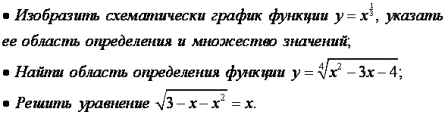
Уровень возможной подготовки выпускника
Тема 4. «Показательная функция» (12 часов)
Раздел математики. Сквозная линия
· Функции
· Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
· Показательная функция.
· Свойства показательной функции.
· График показательной функции.
· Показательные уравнения.
· Показательные неравенства.
· Системы показательных уравнений и неравенств.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Иметь наглядное представления об основных свойствах функций.
· Изображать графики показательной функции.
· Описывать свойства показательных функций, опираясь на график.
· Уметь решать показательные уравнения и неравенства.
Уровень возможной подготовки обучающегося
· Иметь наглядное представления об основных свойствах функций, иллюстрировать их с помощью графических изображений.
· Изображать графики показательной функции. Описывать свойства этих функций, опираясь на график.
· Уметь использовать свойства функции для сравнения и оценки ее значений.
· Уметь решать показательные уравнения и неравенства, применяя различные методы их решения.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 5. «Логарифмическая функция» (17 часов)
Раздел математики. Сквозная линия
· Вычисления и преобразования
· Функции
· Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
· Логарифмы.
· Свойства логарифмов.
· Десятичные и натуральные логарифмы.
· Логарифмическая функция.
· Свойства логарифмической функции.
· График логарифмической функции
· Логарифмические уравнения.
· Логарифмические неравенства.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Иметь наглядное представления об основных свойствах функций.
· Изображать графики логарифмической функции.
· Описывать свойства логарифмических функций, опираясь на график.
· Уметь решать логарифмические уравнения и неравенства, используя стандартный алгоритм их решения.
Уровень возможной подготовки обучающегося
· Иметь наглядное представления об основных свойствах логарифмических функций, иллюстрировать их с помощью графических изображений.
· Изображать графики логарифмических функций. Описывать свойства этих функций, опираясь на график.
· Уметь использовать свойства логарифмической функции для сравнения и оценки ее значений.
· Уметь решать логарифмические уравнения и неравенства, применяя различные методы их решения.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 6 «Алгебраические уравнения. Системы нелинейных уравнений» (16 часов)
Раздел математики. Сквозная линия
· Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
· Решение рациональных уравнений.
· Примеры решения уравнений высших степеней; методы замены переменной, разложение на множители.
· Система уравнений; решение системы; примеры решения нелинейных систем.
· Решение текстовых задач алгебраическим способом.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Уметь решать квадратные, рациональные уравнения, сводящиеся к ним.
· Уметь решать системы двух линейных уравнений и несложные нелинейные системы.
· Уметь решать текстовые задачи алгебраическим методом.
Знать как используются уравнения и системы уравнений на практике.
Знать понятие функции, свойства функций.
Уровень возможной подготовки обучающегося
· Уметь решать алгебраические уравнения высших степеней и уравнения, сводящиеся к ним.
· Уметь решать системы линейных и нелинейных уравнений.
· Уметь решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 7. «Тригонометрические формулы» (25 часов)
Раздел математики. Сквозная линия
· Вычисления и преобразования
Обязательный минимум содержания образовательной области математика
· Радианная мера угла. Поворот точки вокруг начала координат.
· Определение синуса, косинуса и тангенса угла.
· Знаки синуса, косинуса и тангенса углов.
· Зависимость между синусом, косинусом и тангенсом одного итого же угла.
· Тригонометрические тождества.
· Формулы сложения
· Синус, косинус и тангенс двойного и половинного угла.
· Формулы приведения.
· Сумма и разность синусов.
· Сумма и разность косинусов.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц.
· Выполнять тождественные преобразования тригонометрических выражений с помощью справочного материала
Уровень возможной подготовки обучающегося
· Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц. Выполнять тождественные преобразования тригонометрических выражений.
· Уметь применять тригонометрические формулы в при решении практических задач
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника
Тема 8. «Тригонометрические уравнения» (19 часа)
Раздел математики. Сквозная лини
· Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
· Тригонометрические уравнения sinx=a, cosx=a, tgx=a.
· Решение тригонометрических уравнений.
· Простейшие тригонометрические неравенства.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
· Уметь решать простейшие тригонометрические уравнения.
Уровень возможной подготовки обучающегося
· Уметь решать тригонометрические уравнения.
· Овладеть некоторыми приемами решения тригонометрических уравнений.
Уровень обязательной подготовки выпускника 
Уровень возможной подготовки выпускника
Тема 9. «Повторение» (18 часов)
Раздел математики. Сквозная линия
· Числа и вычисления
· Вычисления и преобразования
· Уравнения и неравенства
· Функции
Обязательный минимум содержания образовательной области математика
Действительные числа.
Корень степени n.
Логарифм.
Степень с действительным показателем.
Тригонометрические выражения.
Решение алгебраических, иррациональных, показательных логарифмических, тригонометрических уравнений, неравенств и их систем.
Числовые функции и их свойства.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Знать определения натурального, целого, рационального, действительного числа. Уметь производить вычисления с этими числами.
Знать определения и свойства арифметического корня n-й степени, логарифма, степени с действительным показателем, тригонометрические формулы. Уметь выполнять преобразования несложных иррациональных, степенных, логарифмических, тригонометрических выражений.
Уметь решать несложные алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы.
Знать свойства степенной, показательной, логарифмической функций и уметь строить их графики.
Уровень возможной подготовки обучающегося
Знать определения натурального, целого, рационального, действительного числа. Уметь производить вычисления с этими числами. Уметь обращать бесконечную периодическую дробь в обыкновенную.
Знать определения и свойства арифметического корня n-й степени, логарифма, степени с действительным показателем, тригонометрические формулы. Уметь выполнять преобразования иррациональных, степенных, логарифмических, тригонометрических выражений.
Уметь решать алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы, применяя различные методы их решений.
Знать свойства степенной, показательной, логарифмической функций и уметь строить их графики. Уметь применять свойства функций при решении различных задач.
Уровень обязательной подготовки выпускника
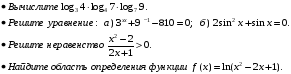

Уровень возможной подготовки выпускника
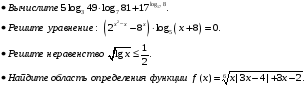
Учебно – тематический план
| № п/п | Раздел | Общее количество часов | Формы подведения итогов |
| 1 | Повторение | 5 |
|
| 2 | Действительные числа | 14 | Контрольная работа №1 |
| 3 | Степенная функция | 14 | Контрольная работа №2 |
| 4 | Показательная функция | 12 | Контрольная работа №3 |
| 5 | Логарифмическая функция | 17 | Контрольная работа №4 |
|
| Алгебраические уравнения. Системы нелинейных уравнений. | 16 | Контрольная работа №5 |
| 6 | Тригонометрические формулы | 25 | Контрольная работа №6 |
| 7 | Тригонометрические уравнения | 19 | Контрольная работа №7 |
| 8 | Повторение | 18 | Итоговая контрольная работа |
|
| Итого: | 140 |
|
Календарно – тематическое планирование
по алгебре и началам анализа в 10 специальном (коррекционном) классе 1 вида
| № | Тема раздела, тема урока | Кол-во часов
| Дата | Основные вопросы, рассматриваемые на уроке | Активизация речевого словаря | ||
| План | Факт | ||||||
|
| Повторение курса 9 класса | 5 |
|
|
|
| |
| 1 | Алгебраические выражения | 1 |
|
| Преобразование алгебраических выражений | Алгебраические выражения | |
| 2-3 | Алгебраические уравнения и системы уравнений | 2 |
|
| Решение уравнений, систем уравнений | Уравнение, система, неизвестное, корни уравнения | |
| 4 | Неравенства | 1 |
|
| Решение неравенств и систем | Неравенство, система, неизвестное | |
| 5 | Функции и графики | 1 |
|
| Построение и исследование графиков функций | Функция, график, абсцисса, ордината | |
|
| Действительные числа | 11+3 |
|
|
|
| |
| 6 | Целые и рациональные числа | 1 |
|
| Преобразование числовых выражений, | Целые и рациональные числа | |
| 7 | Действительные числа | 1 |
|
| Действительные числа | Целые и рациональные числа | |
| 8-9 | Бесконечно убывающая геометрическая прогрессия | 2 |
|
| Геометрическая прогрессия, понятие предела бесконечно убывающих числовых рядов | Прогрессия, десятичные дроби, геометрическая прогрессия | |
| 10-12 | Арифметический корень натуральной степени | 3 |
|
| Определение корня, преобразование выражений, содержащих корни | Корень, степень, арифметический корень n-ой степени | |
| 13-16 | Степень с рациональным и действительным показателями | 4 |
|
| Преобразование выражений, содержащих степень с действительным показателем | Корень, степень, показатель степени | |
| 17-18 | Обобщающий урок по теме: «Действительные числа» | 2 |
|
| Подготовка к контрольной работе | Целые, рациональные, действительные числа, геометрическая прогрессия, степень | |
| 19 | Контрольная работа № 1 по теме: «Действительные числа» | 1 |
|
| Контроль знаний и умений |
| |
|
| Степенная функция | 10+4 |
|
|
|
| |
| 20-21 | Степенная функция, ее свойства и график | 2 |
|
| Определение степенной функции, свойства, график | Степень, корень п-ой степени | |
| 22 | Взаимно обратные функции | 1 |
|
| Определение обратной функции, взаимно обратные функции | Функции, свойства | |
| 23-24 | Равносильные уравнения и неравенства | 2 |
|
| Определение равносильных уравнений и неравенств, их решение | Уравнения, неравенства | |
| 25-27 | Иррациональные уравнения | 3 |
|
| Определение иррационального уравнения, его решение | Уравнения, способы решения | |
| 28-30 | Иррациональные неравенства | 3 |
|
| Решение иррациональных неравенств | Неравенства, свойства неравенств | |
| 31-32 | Обобщающий урок по теме: «Степенная функция» | 2 |
|
| Повторение степенной функции |
| |
| 33 | Контрольная работа № 2 по теме: «Степенная функция» | 1 |
|
| Контроль знаний и умений |
| |
|
| Показательная функция | 10+2 |
|
|
|
| |
| 34-35 | Показательная функция, ее свойства и график | 2 |
|
| Определение показательной функции, ее свойства и график | Степень, степенная функция | |
| 36-37 | Показательные уравнения | 2 |
|
| Определение показательного уравнения, его решение | Уравнение, степень | |
| 38-39 | Показательные неравенства | 2 |
|
| Решение показательных неравенств | Неравенства и его свойства | |
| 40-42 | Системы показательных уравнений и неравенств | 3 |
|
| Решение систем показательных уравнений и неравенств | Системы уравнений и неравенств, их способы решения | |
| 43-44 | Обобщающий урок по теме: «Показательная функция» | 2 |
|
| Подготовка к контрольной работе | Определение показательного уравнения, его решение, решение показательных неравенств, решение систем показательных уравнений и неравенств | |
| 45 | Контрольная работа № 3 по теме: «Показательная функция» | 1 |
|
| Контроль знаний и умений |
| |
|
| Логарифмическая функция | 14+3 |
|
|
|
| |
| 46-47 | Логарифмы | 2 |
|
| Определение логарифма | Степень, основание степени | |
| 48-49 | Свойства логарифмов | 2 |
|
| Свойства логарифмов | Степень, основание степени | |
| 50-51 | Десятичные и натуральные логарифмы | 2 |
|
| Определение десятичных натуральных логарифмов, преобразование выражений | Логарифмы, степень | |
| 52-53 | Логарифмическая функция, ее свойства и график | 2 |
|
| Определение логарифмической функции, ее свойства и график | Показательная функция, графики, свойства | |
| 54-56 | Логарифмические уравнения | 3 |
|
| Логарифмическое уравнение и его решение | Способы решения уравнений | |
| 57-59 | Логарифмические неравенства | 3 |
|
| Решение логарифмических неравенств | Способы решения неравенства | |
| 60-61 | Обобщающий урок по теме: «Логарифмическая функция» | 2 |
|
| Подготовка к контрольной работе | Свойства логарифмов, логарифмическое уравнение и его решение, решение логарифмических неравенств | |
| 62 | Контрольная работа № 4 по теме: «Логарифмическая функция» | 1 |
|
| Контроль знаний и умений |
| |
|
| Алгебраические уравнения. Системы нелинейных уравнений. | 13+3 |
|
|
|
| |
| 63 | Деление многочленов | 1 |
|
| Алгоритм деления многочлена на многочлен |
| |
| 64-65 | Решение алгебраических уравнений | 2 |
|
| Способы решения алгебраических уравнений | Определение целого уравнения и его корни; степень уравнения; определение дробного рационального уравнении и его корни;
| |
| 66-68 | Уравнения, сводящиеся к алгебраическим | 3 |
|
| Решение целых уравнений с одной переменной с помощью разложения на множители; с помощью введения вспомогательной переменной; дробно рациональные уравнения;
| Определение целого уравнения и его корни; степень уравнения; определение дробного рационального уравнении и его корни;
| |
| 69-71 | Системы нелинейных уравнений с двумя неизвестными | 3 |
|
| Определение уравнения с двумя переменными и его график | Уравнение второй степени с двумя переменными
| |
| 72-73 | Различные способы решения систем уравнений | 2 |
|
| Определение системы уравнений второй степени | Простейшие системы, содержащие уравнение второй степени с двумя переменными способом подстановки; | |
| 74-75 | Решение задач с помощью систем уравнений | 2 |
|
| Решение задач с помощью систем уравнений второй степени; | Текстовые задачи с помощью составления систем уравнений второй степени | |
| 76-77 | Обобщающий урок по теме: «Алгебраические уравнения. Системы нелинейных уравнений» | 2 |
|
| Решение целых уравнений с одной переменной с помощью разложения на множители; с помощью введения вспомогательной переменной; дробно рациональные уравнения; решение задач с помощью систем уравнений второй степени; | Определение целого уравнения и его корни; степень уравнения; определение дробного рационального уравнении и его корни;
| |
| 78 | Контрольная работа № 5 по теме: «Алгебраические уравнения. Системы нелинейных уравнений» | 1 |
|
| Контроль знаний и умений |
| |
|
| Тригонометрические формулы | 21+4 |
|
|
|
| |
| 79 | Радианная мера угла | 1 |
|
| Радианная мера угла, соотношение градусной меры и радианной | Измерение углов, радианная мера | |
| 80-81 | Поворот точки вокруг начала координат | 2 |
|
| Поворот, угол | Система координат, измерение углов | |
| 82-83 | Определение синуса, косинуса и тангенса угла | 2 |
|
| Определение синуса, косинуса и тангенса угла | Прямоугольный треугольник, синус, косинус, тангенс | |
| 84 | Знаки синуса, косинуса и тангенса | 1 |
|
| Определение знаков синуса, косинуса и тангенса по четвертям | Система координат, положительное и отрицательное направления | |
| 85-86 | Зависимость между синусом, косинусом и тангенсом одного и того же угла | 2 |
|
| Соотношения между синусом, косинусом и тангенсом одного и того же угла | Тождества, формулы, синус, косинус, тангенс | |
| 87-89 | Тригонометрические тождества | 3 |
|
| Применение тригонометрических тождеств для решения задач | Тождества и формулы | |
| 90 | Синус, косинус и тангенс углов | 1 |
|
| Определение значений синуса, косинуса и тангенсам углов | Четные, нечетные функции, синус, косинус, тангенс | |
| 91-93 | Формулы сложения | 3 |
|
| Формулы сложения, применение к преобразованию выражений | Формулы | |
| 94-95 | Синус, косинус и тангенс двойного угла | 2 |
|
| Формулы двойного угла, решение заданий с использованием данных формул | Формулы, синус, косинус, тангенс | |
| 96 | Синус, косинус и тангенс половинного угла | 1 |
|
| Формулы и их применение при решении задач | Формулы, синус, косинус, тангенс | |
| 97-98 | Формулы приведения | 2 |
|
| Применение формул приведения | Формулы приведения | |
| 99-100 | Сумма и разность синусов. Сумма и разность косинусов | 2 |
|
| Формулы суммы и разности синусов и косинусов | Формулы, синус, косинус, сумма, разность | |
| 101-102 | Обобщающий урок по теме: «Тригонометрические формулы» | 2 |
|
| Подготовка к контрольной работе, применение тригонометрических формул | Формулы и тождества | |
| 103 | Контрольная работа № 6 по теме: « Тригонометрические формулы» | 1 |
|
| Контроль знаний и умений |
| |
|
| Тригонометрические уравнения | 13+6 |
|
|
|
| |
| 104-106 | Уравнение cos x = a | 3 |
|
| Решение уравнения вида cos x = a, определение arccos | Обратная функция, значение углов, косинус, уравнение | |
| 107-109 | Уравнение sin x = a | 3 |
|
| Решение уравнения вида sin x = a определение arcsin | Тригонометрические формулы, решение уравнений, синус | |
| 110-112 | Уравнение tq x = a | 3 |
|
| Решение уравнения вида tq x = a, определение arc tq | Тригонометрические формулы, решение уравнений, тангенс | |
| 113-117 | Решение тригонометрических уравнений | 5 |
|
| Различные способы решения тригонометрических уравнений | Уравнение, корень | |
| 118-119 | Примеры решения простейших тригонометрических неравенств | 2 |
|
| Решение тригонометрических неравенств | Неравенства | |
| 120-121 | Обобщающий урок по теме: « Тригонометрические уравнения» | 2 |
|
| Подготовка к контрольной работе, применение тригонометрических формул | Различные способы решения тригонометрических уравнений | |
| 122 | Контрольная работа № 7 по теме: « Тригонометрические уравнения» | 1 |
|
| Контроль знаний и умений |
| |
|
| Повторение. | 13+5 |
|
| Обобщить и систематизировать знания и умения за курс алгебры и начала анализа 10 класса |
| |
| 123-125 | Действительные числа | 3 |
|
| Геометрическая прогрессия, понятие предела бесконечно убывающих числовых рядов. Определение корня, преобразование выражений, содержащих корни. Преобразование выражений, содержащих степень с действительным показателем |
| |
| 126-128 | Степенная функция | 3 |
|
| Определение степенной функции, свойства, график. Определение иррационального уравнения, его решение. Решение иррациональных неравенств |
| |
| 129-131 | Показательная функция | 3 |
|
| Определение показательного уравнения, его решение. Решение показательных неравенств. Решение систем показательных уравнений и неравенств. |
| |
| 132-134 | Логарифмическая функция | 3 |
|
| Свойства логарифмов. Определение логарифмической функции, ее свойства и график. Логарифмическое уравнение и его решение. Решение логарифмических неравенств. |
| |
| 135-136 | Тригонометрические формулы | 2 |
|
| Соотношения между синусом, косинусом и тангенсом одного и того же угла. Формулы и их применение при решении задач. |
| |
| 137 | Итоговая контрольная работа | 1 |
|
| Контроль знаний и умений |
| |
| 138 | Консультация | 1 |
|
| Решение ЕГЭ |
| |
| 139 | Консультация | 1 |
|
| Решение ЕГЭ |
| |
| 140 | Консультация | 1 |
|
| Решение ЕГЭ |
| |

 Получите свидетельство
Получите свидетельство Вход
Вход



 и -
и - 









 Адаптированная рабочая программа для глухих детей по алгебре и началам анализа 10 класс (148.99 KB)
Адаптированная рабочая программа для глухих детей по алгебре и началам анализа 10 класс (148.99 KB)
 0
0 654
654 16
16 Нравится
0
Нравится
0


