3D построения в Mathcad

РЕФЕРАТ НА ТЕМУ

«3D построения в Mathcad»

Содержание

Введение 3

1. Общие сведения о Mathcad. 3

2. Построение трехмерных поверхностей в системе Mathcad. 6

Заключение 11

Список использованных источников 12

MathCad – это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования.

В системе MathCAD для вывода и интерпретации результатов расчета используется двухмерная (2D) и трехмерная (3D) графика. Двухмерная графика подразумевает графическое представление в декартовой (График Х-У) и полярной (Полярный график) системе координат. 3D графика используется для построения трехмерных поверхностей (Surface Plot), контурных графиков (Contour Plot), 3D гистограмм (3D Bar Chart) и других трехмерных объектов. Соответствующие пиктограммы изображены в палитре «Graph (Графики)».

1. Общие сведения о Mathcad.

Mathcad – система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается лёгкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Некоторые из математических возможностей Mathcad основаны на подмножестве системы компьютерной алгебры Maple (MKM, Maple Kernel Mathsoft). Начиная с 14 версии – использует символьное ядро MuPAD.

Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования.

Несмотря на то, что эта программа, в основном, ориентирована на пользователей, не являющихся программистами, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования путём использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов.

Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Среди возможностей Mathcad можно выделить:

• Решение дифференциальных уравнений, в том числе и численными методами;

• Использование греческого алфавита как в уравнениях, так и в тексте;

• Выполнение вычислений в символьном режиме;

• Выполнение операций с векторами и матрицами;

• Символьное решение систем уравнений;

• Аппроксимация кривых;

• Выполнение подпрограмм;

• Поиск корней многочленов и функций;

• Проведение статистических расчётов и работа с распределением вероятностей;

• Поиск собственных чисел и векторов;

• Вычисления с единицами измерения;

• Интеграция с САПР-системами, использование результатов вычислений в качестве управляющих параметров;

• Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.);

Рассмотрим подробнее построение трёхмерных графиков функций в системе Mathcad.

1. Построение трехмерных поверхностей в системе Mathcad.

3D графика служит для построения трехмерных поверхностей, задаваемых функцией двух переменных F(x,y). Процедура построения поверхности заключается в следующем:

Быстрое построение является наиболее легким способом построения поверхностей. Для этого необходимо:

1. Задаем функцию двух переменных f(x,y) и область изменения параметров x a,b и yc,d . Затем определяем количество точек по осям N, в которых будут определяться значения функции.

2. Выбрать команду главного меню «Вставка», «График», выбрать вид графика «поверхность» на панели инструментов «Графики».

3. В шаблон трехмерного графика ввести имя функции без указания аргументов.

Перечень различных графиков содержит подменю Graph в позиции Insert главного меню. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения того или иного вида достаточно задать тип графика. В подменю Graph содержится список из семи основных типов графиков, основные из которых применялись для решения задач построений и их иллюстраций.

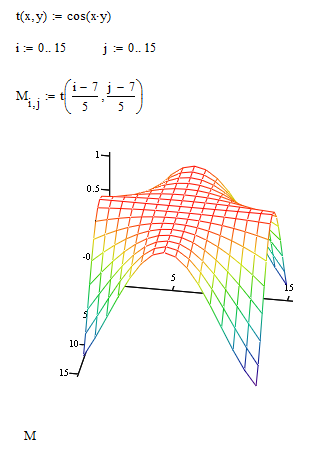
Пример 1. Построить график функции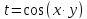

Пример 2. Построить график функции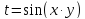

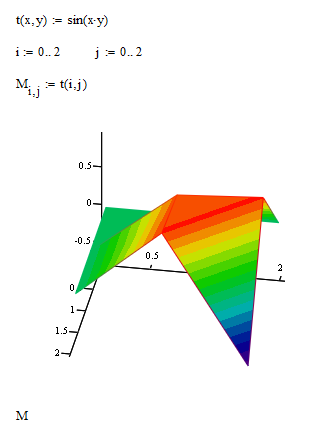
Пример 3.

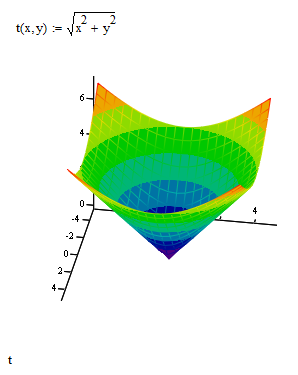
Пример 4. Постройте график параметрически заданной поверхности.

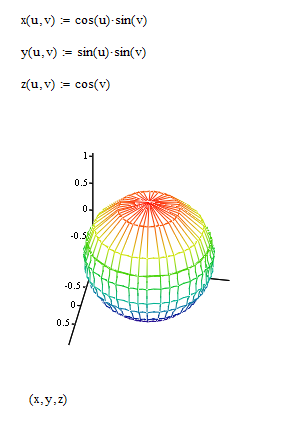
Mathcad – это мощная и в то же время простая универсальная среда для решения задач в различных отраслях науки и техники, финансов и экономики, физики и астрономии, математики и статистики.

Mathcad позволяет выполнять как численные, так и аналитические (символьные) вычисления, при этом точность, с которой отображается результат, задается пользователем, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства научной графики.

В пакете Mathcad представлен обширный набор инструментов для реализации графических методов решения математических задач, которые использовались нами в построениях. Графики в Mathcad являются универсальными и легкими в использовании. Пакет позволяет строить графики разных типов: графики в декартовых координатах, графики в полярных координатах, строить поверхности, строить линии уровня, картины векторных полей, трехмерные гистограммы, точечные графики.

1. Акишин, Б. А. Прикладные математические пакеты. Часть 1. MathCAD / Б. А. Акишин, Н. Х. Эркенов. – СПб. : РадиоСофт, 2009. – 132 с.

2. Алексеев, Е. Р. Mathcad 12 / Е. Р. Алексеев, О. В. Чеснокова. – М.: НТ Пресс, 2005. – 352 с.

3. Бутенков, С.А. Методические указания к использованию системы

MathCad в практических занятиях по курсу высшей математики / C. А Бутенков. – СПб. : Таганрог: ТРТУ, 1995. – 450 с.

1. Графика в системе MathCAD [Электронный ресурс]. – Режим доступа :http://detc.ls.urfu.ru/assets/amath0021/l3.htm#l3.1

2. Крестелев, А. И. MathCAD Ч.1: учеб. пособие / А. И. Крестелев. – Самара: Самар. гос. техн. ун-т, 2010. – 58 с.