Видеоурок по математике «Целые и рациональные числа»

Число — важнейшее математическое понятие, меняющееся на протяжении веков. Вы уже знаете, что числа, которые мы используем в счёте, называют натуральными. Кстати, натуральные числа — это один из первых математических объектов, который стал изучать человек, так как повседневная жизнь требовала использования натуральных чисел на практике, и, в частности, в счёте. Поэтому и изучение математики в школе мы начинали именно со знакомства с натуральными числами.

С понятием натуральных чисел мы с вами разобрались, а теперь давайте перейдём к действиям с ними. И ответим на вопрос: какие числа получают при сложении и умножении натуральных чисел?

Конечно же, вам не составит труда ответить на этот вопрос. И вы сразу скажете, что при сложении натуральных чисел всегда получают натуральные числа. И при умножении натуральных чисел тоже всегда получают натуральные числа.

Тогда возникает новый вопрос: а какие числа мы получим при вычитании и делении натуральных чисел?

Так вот, при нахождении разности и частного натуральных чисел не всегда получаются натуральные числа. В связи с этим математикам пришлось расширять знания, связанные с числами.

Если мы добавим к натуральным числам нуль и отрицательные числа (то есть числа, которые противоположны натуральным), то множество натуральных чисел расширится до множества целых чисел.

Мы с вами разобрались с понятием целых чисел, а теперь давайте перейдём к действиям с ними. Понятно, что при сложении, вычитании и умножении целых чисел всегда получают целые числа. Чего нельзя сказать о делении целых чисел. При нахождении частного двух целых чисел в результате не всегда получают целые числа.

Следовательно, понятия, связанные с числами, пришлось расширять дальше. Так, множество целых чисел расширили, введя множество рациональных чисел.

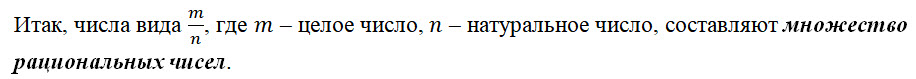
Одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.

Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби. Такие числа можно записать в виде бесконечной десятичной дроби. Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру — её периодом.

Тогда можем сделать такой вывод: любая периодическая дробь — это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр — период дроби.

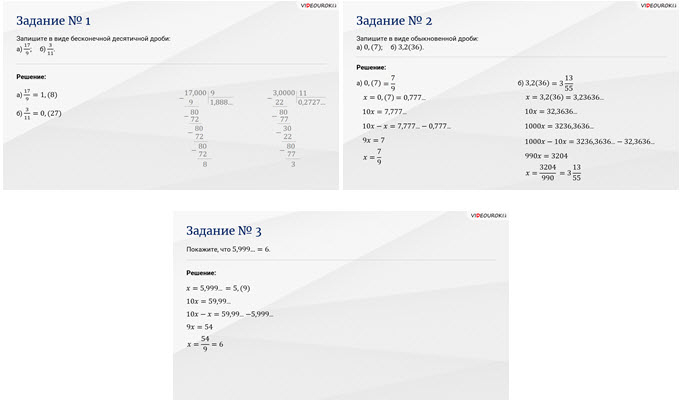
А теперь давайте приступим к практической части нашего урока.