Видеоурок «Параллельные прямые в пространстве»

Ранее в планиметрии мы с вами уже рассматривали взаимное расположение двух прямых на плоскости. Напомним, что возможны три случая.

Первый случай. Прямые параллельны, то есть две прямые не имеют общих точек.

Второй случай. Прямые пересекаются, то есть две прямые имеют одну общую точку.

И третий случай. Прямые совпадают, то есть имеют более чем одну общую точку.

Теперь перейдём к стереометрии. Напомним, что стереометрия изучает свойства фигур в пространстве.

Рассмотрим прямоугольный параллелепипед 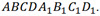Как вы уже знаете, параллелепипед — это пространственное тело.

Прямые, на которых лежат его ребра, например параллельны. Прямые, через которые проходят диагонали его грани, например

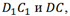пересекаются. А вот прямые, на которых лежат диагональ параллелепипеда 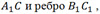называются скрещивающимися.

Сделаем вывод: две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.

Пересекающиеся и параллельные прямые задают некоторую плоскость. Скрещивающиеся прямые — это прямые, через которые нельзя провести плоскость.

Давайте подробно остановимся на случае с параллельными прямыми в пространстве.

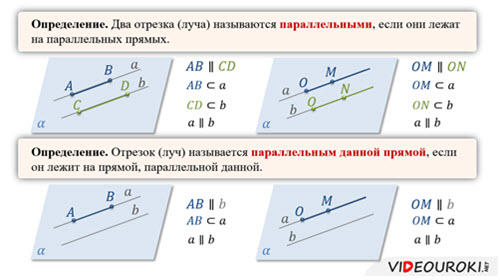
Запишем определение параллельных прямых в пространстве.

Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении очень важна. Так как в стереометрии мы с вами рассматриваем трёхмерное пространство и, если две прямые лежат в разных плоскостях, нельзя говорить про их параллельность. Параллельными прямые могут быть, только если лежат в одной плоскости.

Приведём несколько примеров параллельных прямых в пространстве.

Запишем определения параллельных отрезков и параллельных лучей в пространстве.

Справедлива теорема о параллельности прямых. Сформулируем и докажем её.

Замечание. Если прямые в пространстве параллельны, то на чертеже они обязательно изображаются параллельными прямыми. А вот если прямые на чертеже изображены параллельными прямыми, то в пространстве эти прямые не обязательно параллельны.