Видеоурок по математике «Понятие правильного многогранника»

Цели урока

Образовательные цели: определить понятие «правильный многогранник», рассмотреть пять видов правильных многогранников.

Развивающие цели: содействовать развитию внимания, воображения, логического мышления, геометрического видения.

Воспитательные цели: воспитать уверенность, целеустремленность, трудолюбие и интерес к изучению математики.

Тип урока: урок объяснения нового материала.

Ход урока

1. Организационный момент:

• приветствие;
• проверка готовности учащихся к уроку;
• организация внимания учащихся.

2. Объяснение нового материала

Прежде чем мы перейдем к изучению вопросов о правильных многогранниках, напомним некоторые уже известные вам понятия.

Вообще, многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.

Скачать видеоурок «Понятие правильного многогранника»

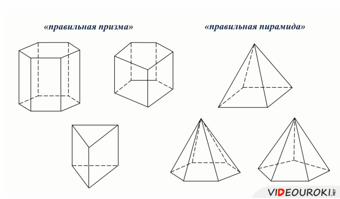
Вам уже знакомы такие словосочетания, как «правильная призма», «правильная пирамида». Оказывается, эти словосочетания знакомых вам понятий образуют совершенно новое, с геометрической точки зрения, понятие.

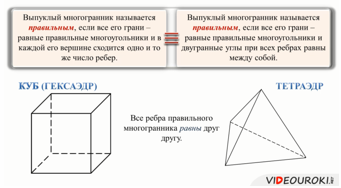
Запишем определение. Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Существует и другое определение правильного многогранника. Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники и двугранные углы при всех ребрах равны между собой.

Оба эти определения используются в математике как равноправные.

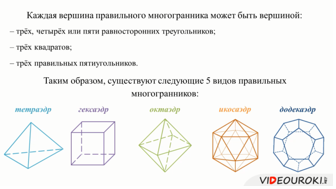
Вообще, существует пять видов правильных многогранников. Два из них мы уже знаем — это куб и тетраэдр.

Существуют следующие пять видов правильных многогранников: тетраэдр, гексаэдр (или куб), октаэдр, икосаэдр, додекаэдр.

Рассмотрим каждый из них.

3. Подведение итогов

На этом уроке мы познакомились с понятием правильного многогранника. Выявили, что существует только пять видов правильных многогранников: тетраэдр, гексаэдр (или куб), октаэдр, икосаэдр и додекаэдр. А также рассмотрели каждый из них.

4. Рефлексия

Хотелось бы узнать: понравился ли вам урок? Что было непонятным на уроке? Что еще вы бы хотели узнать?

5. Домашнее задание