Тригонометрические функции углового аргумента

Цели урока:

обучающая: рассмотреть тригонометрические функции углового аргумента; показать связь между тригонометрическими функциями углового и числового аргумента; повторить связи между элементами прямоугольного треугольника; ввести понятие «угловая мера угла», «радианная мера угла»; показать формулы перехода от радианной меры угла к угловой и обратно.

развивающая: развитие умения применять полученные знания на практике, развитие умения быстро переходить от радианной меры угла к угловой и обратно.

воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению математики.

Методы:

словесный — беседа;

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный (письменный) опрос, решение задач).

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

На предыдущих уроках, мы с вами познакомились с тригонометрическими функциями числового аргумента тэ. Напомним их:

3. Объяснение нового материала.

Сегодня мы будем рассматривать тригонометрические функции углового аргумента. Прежде чем перейти к рассмотрению новой темы, давайте вспомним как и зачем появились понятия синус, косинус, тангенс и котангенс.

Появились эти понятия тогда, когда стало необходимым вычислить высоту дерева, не залезая на него.

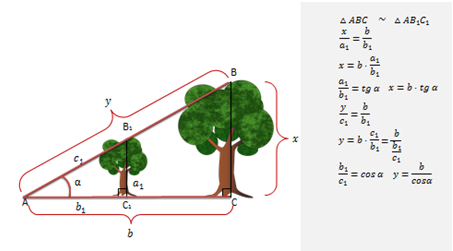
С понятиями синус, косинус, тангенс, котангенс мы знакомились в прямоугольном треугольнике. Давайте вспомним основные правила, связанные с этими величинами.

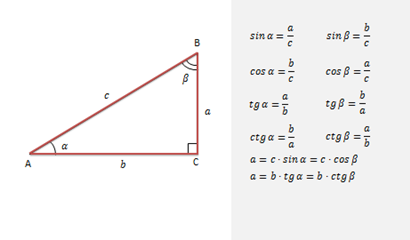
Возьмем угол α и разместим его на числовой окружности так, чтобы вершина угла совпала с началом координат.

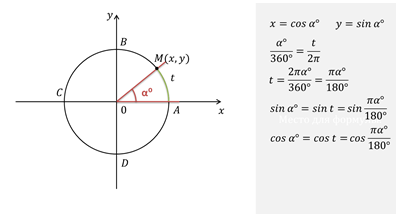
Рассмотрим пример.

Рассмотрим несколько примеров.

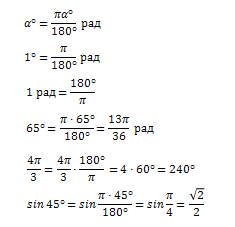
Изобразим числовую окружность и проведем угол величиной в один градус.

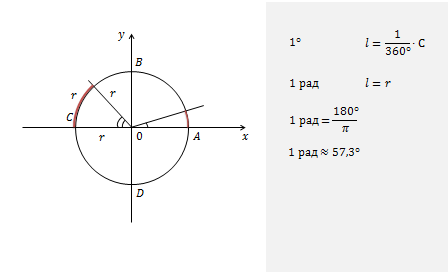
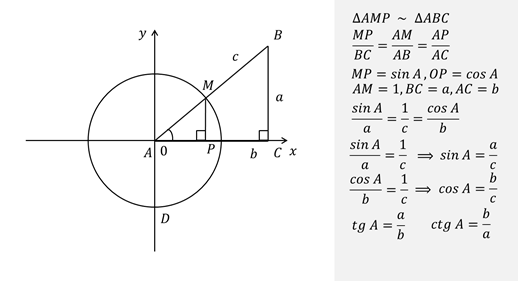
Покажем, что изученные нами ранее тригонометрические функции числового аргумента и тригонометрические функции углового аргумента — это одно и тоже.

Изобразим числовую окружность и разместим в ней треугольник АВС так, чтобы вершина, а совпала с началом координат.

Выполните упражнения:

4. Решение задач.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

6. Домашнее задание.