Прямоугольный параллелепипед

Цели урока:

1) Обучающая: формировать представления о прямоугольном параллелепипеде и кубе, о свойствах граней и ребер прямоугольного параллелепипеда, куба; ввести понятия грань, вершина, ребро, измерения, развертка.

2) Развивающая: создать условия для развития пространственного мышления; развивать умения сравнения и обобщения.

3) Воспитывающая: содействовать воспитанию интереса к математике и развитию культуры речи.

Тип урока: изучение нового материала с первичным закреплением.

План урока:

1. Организационный этап.

2. Актуализация опорных знаний.

3. Этап получения новых знаний.

4. Этап обобщения и закрепления нового материала.

5. Рефлексия.

6. Заключительный этап.

Ход урока:

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы узнать, как вы настроены к работе на уроке.

2. Актуализация опорных знаний:

Учитель показывает и раздает на каждый стол модели прямоугольных параллелепипедов.

­­- Кто знает, как правильно называются эти предметы в математике?

— Нарисуйте прямоугольный параллелепипед на доске.

Откройте тетради и запишите число и тему нашего урока.

3. Этап получения знаний:

Тема нашего урока «Прямоугольный параллелепипед». Сегодня на уроке мы узнаем, какую фигуру называют прямоугольным параллелепипедом. Рассмотрим, какими измерениями обладает данная фигура, а также рассмотрим его некоторые свойства.

Нас окружают тела. Они имеют самую разнообразную форму. В математике, прежде всего, изучают некоторый определенный набор тел стандартной формы. Посмотрите на экран — это такие фигуры как призма, цилиндр, шар, пирамида и конус. Каждую из этих фигур мы рассмотрим в будущем, а сегодня же мы остановимся на рассмотрении призмы, или конкретно — прямоугольного параллелепипеда.

Представление о прямоугольном параллелепипеде дают, например, спичечный коробок, холодильник, шкаф и другие тела. Школьный кабинет, в котором мы сейчас с вами находимся, также имеет форму прямоугольного параллелепипеда. Обратите внимание, на экране на первом рисунке изображен прямоугольный параллелепипед, а на втором рисунке — его математическое представление — изображение.

Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников, каждый из которых называют гранью прямоугольного параллелепипеда. Стороны этих прямоугольников называются ребрами, а вершины прямоугольников — вершинами прямоугольного параллелепипеда. Заметьте, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.

Посмотрите, на экране изображен прямоугольный параллелепипед, его противоположные грани не имеют общих точек, они равны между собой. Запомните, противоположные грани прямоугольного параллелепипеда равны. Нижнюю и верхнюю грани прямоугольного параллелепипеда называют его основаниями, остальные грани — боковыми гранями. Названия «нижняя грань», «верхняя грань», «боковая грань» условны. Например, на экране изображен один и тот же параллелепипед, а его верхние грани на рисунках различны.

В каждой вершине прямоугольного параллелепипеда сходятся три ребра. Такие ребра называют длиной, шириной и высотой прямоугольного параллелепипеда. Вместе их называют измерениями параллелепипеда. Названия «длина», «ширина» и «высота» также условны. На рисунке изображен один и тот же прямоугольный параллелепипед, а его высотой, например, названы разные ребра.

Прямоугольный параллелепипед, у которого все ребра равны, называется кубом. Все грани куба — равные между собой квадраты. Поэтому поверхность куба состоит из 6 равных квадратов.

Тело имеет разные свойства. Одним из них является масса, которую находят с помощью весов. Другим свойством тела является площадь поверхности. Обозначим измерения прямоугольного параллелепипеда таким образом: a — его длина, b — ширина и c — высота. Тогда с помощью этих обозначений запишем формулу площади поверхности прямоугольного параллелепипеда: S=2(a∙b+a∙c+b∙c), что видно также из развертки поверхности прямоугольного параллелепипеда на плоскость.

Если ребро куба равно а, то его поверхность состоит из 6 одинаковых квадратов, каждый из которых имеет сторону длиной а. Поэтому площадь поверхности куба можно записать так: .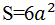

4. Этап обобщения и закрепления нового материала.

Итак, сделаем основные выводы:

Сегодня на уроке мы узнали, какую фигуру называют прямоугольным параллелепипедом. Рассмотрели, какими измерениями обладает данная фигура, а также рассмотрели его свойства. А также познакомились с кубом и его особенностями.

Для закрепления материала ответьте на вопросы:

Приведите примеры предметов, имеющих форму прямоугольного параллелепипеда. Сколько граней имеет прямоугольный параллелепипед? Какую форму имеют грани прямоугольного параллелепипеда? Сколько ребер у прямоугольного параллелепипеда? Какими измерениями обладает прямоугольный параллелепипед? Сколько у него вершин? Какую фигуру называют кубом?

5. Рефлексия.

Хотелось бы узнать, понравился ли вам урок? Что было не понятным на уроке? Что еще бы вы хотели узнать?

6. Домашнее задание: § 4 п. 20 (№ 793, 813, 814)

Дополнительные задания:

Математический диктант (в скобках 2-ой вариант)

№ 1. Сколько граней (измерений) имеет прямоугольный параллелепипед?

№ 2. Закончите предложение: «Каждая грань прямоугольного параллелепипеда имеет форму …» («Куб — прямоугольный параллелепипед, у которого …»).

№ 3. Сколько вершин (ребер) имеет прямоугольный параллелепипед)

№ 4. Запишите формулу площади поверхности прямоугольного параллелепипеда (куба).

Взаимопроверка. Выставление оценок.