Приведение дробей к общему знаменателю

Цель урока: закрепить основное свойство дроби, научить учащихся применять это свойство на практике приведения к общему знаменателю дробей, показать связь между приведением дробей к общему знаменателю и НОКом знаменателей дробей.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний

Учитель фронтально опрашивает учащихся о основном свойстве дроби. Вспоминают понятие НОКа и способы нахождения НОКа двух чисел:

Поможет нам разобраться с этой темой основное свойство дроби, которое, напомню, звучит следующим образом:

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Так, например, по основному свойству дробь 2/3 можно привести к знаменателю 6, умножив и числитель, и знаменатель на 2. Эту дробь можно привести и к знаменателю 9, и 12, и к любому другому числу, кратному 3.

Напомним, что дроби можно приводить только к тем знаменателям, которые кратны исходным.

Ученики по очереди называют числа, к которым можно привести знаменатель дроби ¾.

Дробь ¾ можно привести к знаменателю 4, 8, 12 и к любому другому числу, кратному 4.

Учитель обращает внимание учеников, что можно обе дроби привести к знаменателю 12.

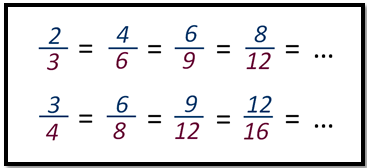
III. Изучение нового материала

Говорят, можно 2/3 и ¾ можно привести к общему знаменателю.

То есть если у нас есть две дроби с разными знаменателями, мы можем сделать так, чтобы знаменатели стали одинаковыми.

Приведение к общему знаменателю понадобится для сложения и вычитания обыкновенных дробей. Кроме того, сравнивать дроби с одинаковыми знаменателями очень просто.

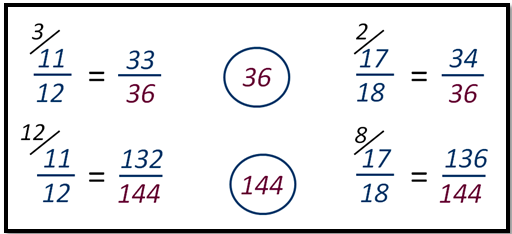
Приведем к общему знаменателю дроби 11/12 и 17/18.

Сначала нам нужно найти такое число, которое делится на каждый из знаменателей.

Учащиеся называют свои варианты чисел.

Таких чисел очень много: 36, 72, 108 и так далее.

Затем приводим к этому числу знаменатели обеих дробей.

То есть дроби можно привести к одинаковому знаменателю 36, 72, 108, 144 и так далее. Удобнее всего выбирать наименьший из возможных общих знаменателей, так как объем вычислений в этом случае будет минимальным.

Например,

11/12=33/36. Чтобы привести 11/12 к знаменателю 36, умножим числитель и знаменатель на 3.

Кстати, число, на которое мы умножаем числитель и знаменатель, называется «дополнительным множителем».

11/12=132/144. Чтобы привести 11/12 к знаменателю 144, умножим числитель и знаменатель на 12. А это немного сложнее, чем умножать на 3.

17/18=34/36. Чтобы привести 17/18 к знаменателю 36, умножим числитель и знаменатель на 2.

17/18=136/144. Чтобы привести 17/18 к знаменателю 144, умножим числитель и знаменатель на 8. Задумались? Поэтому не усложняйте сами себе задачу. Выбирайте наименьший общий знаменатель.

Ученики делают вывод о рациональности приведения дробей к наименьшему общему знаменателю.

Для чисел 12 и 18 число 36 будет наименьшим общим кратным.

IV.Закрепление и практическое применение знаний

В математике существует много способов нахождения общего кратного чисел, а значит общего знаменателя для дробей.

Поэтому, если перед вами стоит задача приведения дробей к общему знаменателю, не торопитесь. Правильно выбранный способ может сократить ваше решение.

Приведем 7/12 и 5/48 к общему знаменателю. Вначале внимательно посмотрите на знаменатели дробей. Возможно, один из них делится на другой.

Ученики делают вывод, то знаменатель 48 делится на 12.

В этом случае дробь с большим знаменателем вообще не надо ни на что умножать. 48 и будет общим знаменателем обеих дробей. А число, полученное в результате деления 48 на 12, будет дополнительным множителем для дроби с меньшим знаменателем.

5/48=5/48

7/12=28/48

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он только в случае, когда один знаменатель делится на другой.

Существует способ, который работает для любых дробей. Суть способа заключается в нахождении наименьшего общего кратного знаменателей. Этот способ используется чаще всего.

Приведем к общему знаменателю дроби 7/410 и 5/861.

Для начала найдём НОК чисел 410 и 861.

Разложим эти числа на простые множители. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь быстро раскладывать на простые множители. Главное — помнить признаки делимости и иметь под рукой таблицу простых чисел.

Теперь записываем все множители одного из чисел, например числа 861. Потом добавляем к ним недостающие множители из разложения другого числа. В этом примере в разложении числа 410 три множителя: 2, 5 и 41. Множитель 41 уже есть в записи, а множителей 2 и 5 нет. Эти недостающие множители мы и добавим к выписанным множителям числа 861.

Наименьшее общее кратное чисел 410 и 861 равно 8610.

Теперь найдем дополнительный множитель для дроби со знаменателем 410. Для этого 8610 делим на 410. Получим 21.

Теперь найдем дополнительный множитель для дроби со знаменателем 861. Для этого 8610 делим на 861. Получим 10.

Последний этап — умножение дробей на дополнительные множители.

Если вам сложно раскладывать числа на множители, находить наименьший общий знаменатель, то следующий способ для вас.

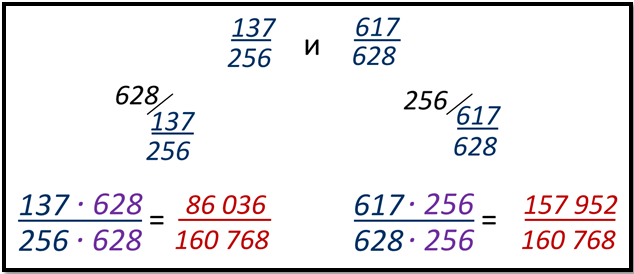
Приведём к общему знаменателю 3/10 и 5/6.

Для этого умножаем первую дробь на знаменатель второй дроби.

3/10=18/60

А вторую — на знаменатель первой.

5/6=50/60

В результате знаменатели обеих дробей стали равными произведению исходных знаменателей.

Этот способ простой для понимания. Но приготовьтесь много считать, если используете этот способ для дробей с большими числами в числителе и знаменателе.

Учитель вместе с учениками проговаривают все возможные способы приведения, все достоинства и недостатки.

№ 275, 278, 283.

V. Подведение итогов урока. Рефлексия

Повторим главное:

Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.

Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.

VI. Домашнее задание

§2, п. 10, № 299, 300.