Дифференцирование функции y=f (kx+m)
Цели урока:
обучающая: рассмотреть правила дифференцирования функции, аргументом которой является функция .
развивающая: развитие умения применять полученные знания на практике, развитие умения быстро вычислять производные функций вида .
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению математики.
Методы:
словесный — беседа;
наглядный — видеоурок, записи на доске;
контролирующий — тестирование или устный (письменный) опрос, решение задач).
Ход урока:
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Проверьте себя:
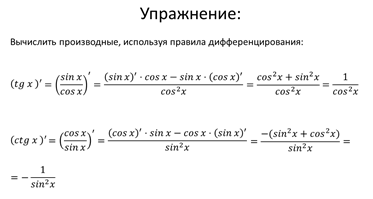
3. Объяснение нового материала.
Ответьте пожалуйста на один вопрос и получите ссылку для скачивания этого урока
Давайте еще раз запишем производные основных функций, которые мы находили на предыдущих уроках и добавим к ним производную тангенса и котангенса.
Обратите внимание, что все функции имеют своим аргументом только одну переменную. А как быть, если аргументом функции является выражение. Например, как найти производную от выражения: Легко заметить, что это сложные функции, то есть аргументом функции является не переменная икс, а функция. В обоих случаях — это линейная функция.
Как мы знаем, производная линейной функции равна коэффициенту перед переменной.
Давайте без доказательства запишем правило:
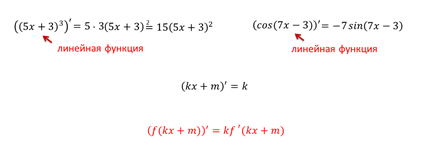
Рассмотрим всю таблицу производных, но аргументом будет линейная функция.
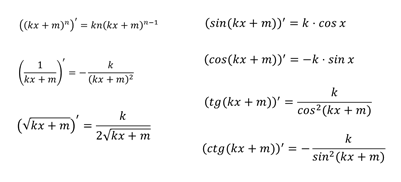
Рассмотрим несколько конкретных примеров.

Рассмотрим еще один пример.

4. Решение задач.
5. Рефлексия
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
6. Домашнее задание.
Получите комплекты видеоуроков + онлайн версии
Похожие записи
 20715
20715 Нравится
0
Нравится
0

 Получите свидетельство
Получите свидетельство Вход
Вход







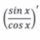


Спасибо
спасибо
Спасибо
Производная сложной функции с опиской
Проверьте запись перед примерами. Две описки, нужно исправить. Спасибо вам за работу!
т