B7. Позиционные системы счисления
В этом уроке мы рассмотрим важные свойства позиционных систем счисления и разберем типовые задачи, которые часто встречаются в заданиях ЕГЭ по информатике.
Начнем с разбора задачи из демоварианта ЕГЭ по информатике 2013 года.
Найти минимальное натуральное десятичное число, которое в троичной и пятеричной системах счисления оканчивается на 0
В этом уроке есть опечатка.
В ответе получили число 50 в троичной сс. Разве есть цифра 5 в этой сс. Ведь алфавит троичной сс-(0 1 2)?
С точки зрения предположения, что сушествует такое целое число все верно. А вот записал я действительно неправильно, нужно было получившееся число, а распределить по разрядам соответствующей системы счисления. Необходимые пометки сделал синим цветом в фрагменте урока Вот посмотрите
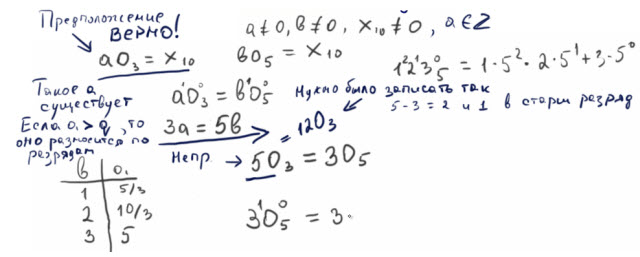
Еще одна задача из группы заданий B7 ЕГЭ по информатике на позиционные системы счисления.
Найти минимальное основание системы счисления q, в которой запись числа 50 трехзначна
Если у вас есть какие то вопросы по теме позиционные системы счисления, или вы не можете решить какие либо задачи В7 ЕГЭ по инфомратике, то можете задать их в комментариях на этой странице
Получите комплекты видеоуроков + онлайн версии
Похожие записи
 10169
10169 Нравится
0
Нравится
0

 Получите свидетельство
Получите свидетельство Вход
Вход







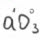


Просто здесь имеется ввиду, что берем ближайший квадрат числа, ведь мы работаем с целыми числами.