На этом уроке мы поговорим о геометрической фигуре, которую называют многоугольником. Уже само слово «многоугольник» указывает на то, что эта фигура имеет много углов.

Давайте посмотрим на следующую фигуру, которая составлена из отрезков AB, BC, CD, DE, EA. Причем смежные отрезки, то есть отрезки AB и BC, BC И CD, CD и DЕ, DE и ЕА, ЕА и АB не лежат на одной прямой, а несмежные отрезки, например, AB и CD, BC и ED, АЕ и CD, не имеют общих точек. Такую фигуру называют многоугольником.
Точки A, B, C, D и Е называются вершинами этого многоугольника, а отрезки AB, BC, CD, DE и ЕА – его сторонами.
Периметром многоугольника называется сумма длин всех его сторон.
Обратите внимание, что рассматриваемый многоугольник имеет 5 вершин и 5 сторон, а поэтому его называют пятиугольником.
Многоугольник с n вершинами называется n-угольником. N-угольник имеет n сторон.
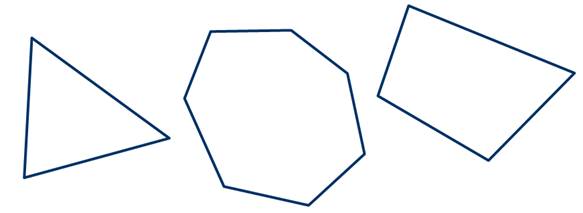
Треугольник является примером многоугольника. Четырёхугольник и семиугольник также являются примерами многоугольников.
А вот следующая фигура не является многоугольником, так как несмежные отрезки и имеют общую точку.

Вернёмся к многоугольнику, рассматриваемому вначале урока.
Две вершины, которые принадлежат одной стороне, например, A и B , B и C, D и Е, называются соседними.
А вот отрезок, соединяющий любые две не соседние вершины, например, AC, BЕ, АD, называется диагональю многоугольника.
Многоугольник разделяет плоскость на две части, а именно, на внутреннюю область многоугольника и на внешнюю.
Следует отметить, что многоугольником также называют фигуру, состоящую из отрезков и внутренней области.
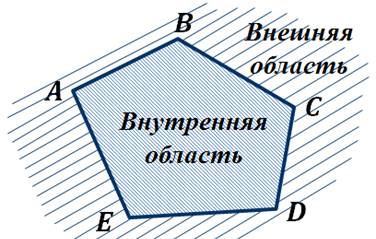
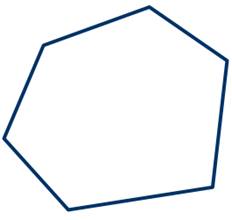
Все многоугольники делят на выпуклые и невыпуклые. Многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через любые две соседние вершины.
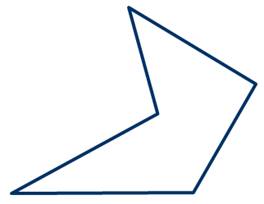
А вот если многоугольник лежит по разные стороны хотя бы от одной прямой, проходящей через две соседние вершины, то его называют невыпуклым.
Теперь давайте выясним, чему же равна сумма углов выпуклого n-угольника.
Давайте возьмём выпуклый четырёхугольник и проведём в нем диагональ, Получили два треугольника.
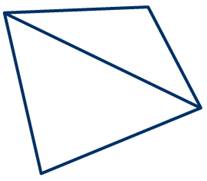
Мы знаем, что сумма углов треугольника равна ста восьмидесяти градусам. А тогда сумма углов выпуклого четырёхугольника равняется сумме углов этих двух треугольников, то есть равняется 180º умножить на 2 и равняется 360º.
Теперь возьмем выпуклый пятиугольник и, проведя в нём две диагонали, разобьём его на три треугольника.

Тогда сумма
углов выпуклого пятиугольника равняется 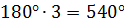 .
.
И возьмем еще, например, выпуклый шестиугольник. Проведём в нем три диагонали.

И получим
четыре треугольника. А тогда сумма углов выпуклого шестиугольника будет равна 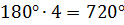 .
.
Таким образом, мы могли бы продолжать находить суммы углов других выпуклых многоугольников. Но обратите внимание, что в четырёхугольнике четыре стороны и мы его разбили на два треугольника. В пятиугольнике: пять сторон – три треугольника. А в шестиугольнике: шесть сторон – четыре треугольника
То есть в каждом случае получается, что треугольников на два меньше, чем сторон у рассматриваемой фигуры.
На
основании этого сделаем вывод: сумма углов выпуклого n-угольника равна 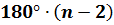 , где n – количество сторон (углов).
, где n – количество сторон (углов).
А теперь давайте решим несколько задач.
Задача. Найти сумму углов выпуклого: а) пятиугольника; б) десятиугольника.
Решение.
Для того чтобы найти сумму углов выпуклого пятиугольника, мы в полученное выше выражение вместо n подставим 5, выполним вычисления и получим 540º.
а) 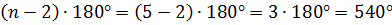 ;
;
А вот чтобы найти сумму углов десятиугольника, подставим в выражение вместо n 10:
б) 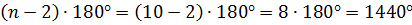 .
.
Ответ: 540 градусов, 1440 градусов.
Задача. Сколько сторон имеет выпуклый многоугольник, каждый угол
которого равен: а) 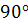 ; б)
; б) 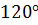 ?
?
Решение.

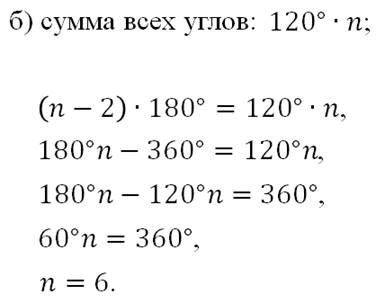
Ответ: 4 и 6.

 Получите свидетельство
Получите свидетельство Вход
Вход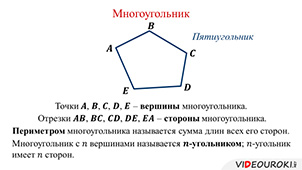



 0
0 15721
15721

