Свойства равнобедренного треугольника

Среди множества треугольников выделяют те, которые имеют особые свойства. К таким треугольникам можно отнести, например, равнобедренные треугольники.

Определение:

Треугольник называется равнобедренным, если две его стороны равны.

Возьмём треугольник АВС, у которого стороны АВ и АС равны.

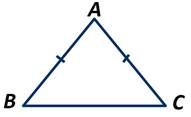
Эти стороны называются боковыми сторонами. Третья сторона ВС называется основанием равнобедренного треугольника. Точка А называется вершиной равнобедренного треугольника, а точки В и С - вершинами при его основании. Угол А называется углом при вершине, а углы В и С - углами при основании.

Определение:

Треугольник, у которого все стороны равны, называется равносторонним.

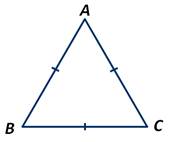
Любой равносторонний треугольник является равнобедренным.

Теорема:

В равнобедренном треугольнике углы при основании равны.

Доказательство:

Пусть АВС равнобедренный треугольник, боковые стороны которого АВ и АС. Докажем, что ∠В=∠С.

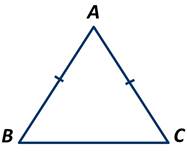
Пусть АF - биссектриса треугольника АВС. Треугольники АВF и АСF равны по первому признаку, так как сторона AF у них общая, стороны АВ и АС равны по условию, ∠ВAF и ∠СAF - равны, так как АF - биссектриса треугольника АВС.

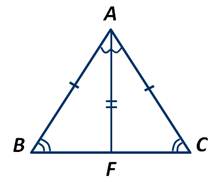
Из равенства треугольников АВF и АСF следует, что ∠В=∠С.

Теорема:

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство:

Пусть треугольник АВС равнобедренный, у которого АВ=АС. Пусть АF - биссектриса этого треугольника.

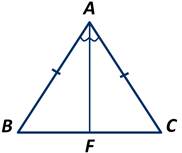
Треугольники АВF и АСF равны по первому признаку, так как сторона AF у них общая, стороны АВ и АС равны по условию, углы ВAF и СAF равны, так как АF - биссектриса треугольника АВС.

Из равенства треугольников следует, что BF равняется CF, то есть F - середина стороны ВС, а следовательно, АF - медиана треугольника АВС.

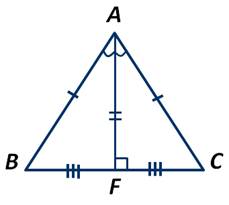
Также из равенства треугольников АВF и АСF следует, что ∠AFB=∠AFC. А так как эти углы смежные и равные, то они прямые. А это означает, что AF является и высотой треугольника АВС. Теорема доказана.

Утверждения:

1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.

2. Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.

Пример.

АВСD - квадрат. Точка Е - середина стороны СD. Доказать, что треугольник ВЕА является равнобедренным.

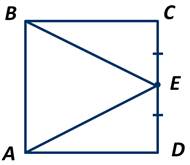
Рассмотрим треугольники ВСЕ и АDE.

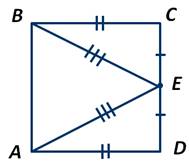
У них ВС=AD, так как все стороны квадрата равны, и СЕ=DE, так как точка Е - середина стороны CD. А ∠ВСЕ=∠ADE, так как все углы квадрата - прямые. Значит, ∆ ВСЕ = ∆ АDE по первому признаку равенства треугольников. То есть у них соответственные стороны равны. Следовательно, ЕВ=ЕА.

Получаем, что треугольник ВЕА имеет две равные стороны ЕВ и ЕА, а значит, он равнобедренный.

Пример.

В равнобедренном треугольнике АВС, где АВ=ВС, Р=20 см., а основание больше боковой стороны на 2 см. Найти стороны треугольника.

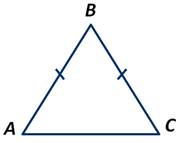
Пусть АВ=ВС=х см., тогда сторона АС=(х+2) см. Получаем:

Тогда АВ=ВС=6 см, а сторона АС=6+2=8 см.