На прошлом уроке мы уже вывели функцию зависимости скорости от времени при равноускоренном движении. Сейчас мы рассмотрим движение с ускорением более подробно.
Как и в случае с положением тела, векторное уравнение можно заменить тремя скалярными уравнениями.
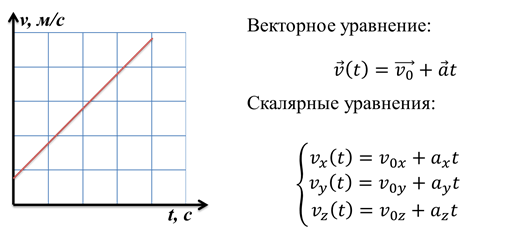
Но в ближайшее время мы будем рассматривать движение тела в одной плоскости, поэтому, нам будет достаточно двух скалярных уравнений.
Мы выяснили, что для описания скорости при движении с постоянным ускорением, достаточно знать начальную скорость и ускорение. Давайте рассмотрим, как будут выглядеть графики функций зависимости ускорения и скорости от времени. При равноускоренном движении ускорение постоянно. Поэтому график зависимости ускорения от времени будет представлять собой прямую горизонтальную линию.

Точно так же, как скорость не зависит от времени при равномерном движении, ускорение не зависит от времени при равноускоренном движении. Заметим, что если мы рассмотрим конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением скорости. Действительно, ведь длина одной из сторон прямоугольника — это ускорение, а длина другой — это время.
Рассмотрим теперь графики зависимости проекции скорости на ось х от времени.
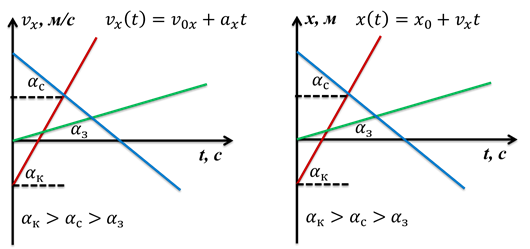
Как вы видите, эти графики аналогичны графикам зависимости координаты от времени при равномерном движении. Как и уравнения, описывающие функции зависимости координаты и скорости от времени очень похожи. Точно также, чем больше угол между графиком скорости и осью времени, тем больше модуль ускорения. Также, из графиков мы можем извлекать информацию о начальной скорости. Начальной скорости будет соответствовать точка пересечения графика с осью скорости.
Теперь давайте попытаемся выяснять, как описать равноускоренное движение. Для этого, используем график зависимости скорости от времени.
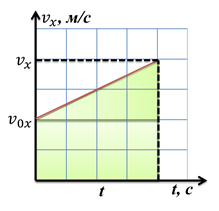
Поскольку ускорение постоянно, график представляет собой прямую. Мы уже говорили о том, что площадь под графиком зависимости проекции скорости от времени равна изменению координаты.
Как мы видим, площадь под графиком представляет собой трапецию. Из геометрии вы знаете, что площадь трапеции равна произведению полусуммы оснований и высоты.
В нашем случае, высота трапеции — это промежуток времени, а основания — это скорости в начальный и конечный моменты времени. Таким образом, получим формулу для изменения координаты х:
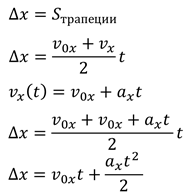
Точно таким же способом мы можем найти уравнение движения для координаты у:
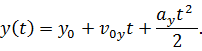
Эти уравнения движения справедливы для любого равноускоренного движения, то есть, для тех случаев, когда ускорение постоянно. Как и всегда, скалярные уравнения можно заменить одним векторным уравнением:
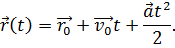
Пример решения задачи:
Птица летит с постоянной
скоростью 8 м/с, а перпендикулярно её движению дует ветер. Ветер сносит птицу с
постоянным ускорением 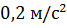 .
Найдите расстояние между начальным положением птицы и её положением через 30 с.
.
Найдите расстояние между начальным положением птицы и её положением через 30 с.
Для начала нам нужно определиться с системой отсчета. Поскольку нас просят найти изменение положения птицы, то логично принять начальное положение птицы за точку отсчёта. Расположим оси координат так, чтобы скорость птицы была направлена вдоль оси х, а дуновение ветра — вдоль оси у.


 Получите свидетельство
Получите свидетельство Вход
Вход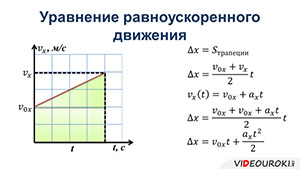



 0
0 13631
13631

