Ещё в младших классах вы сталкивались с тем, что иногда необходимо складывать скорости. Например, если две машины едут навстречу друг другу, то скорость их сближения — это сумма скоростей первой и второй машины.

Если же они двигаются в одном направлении, то скорость их сближения (или удаления) будет определяться разностью скоростей. Как мы уже говорили, решающее значение имеет выбор системы отсчёта.

Закон сложения скоростей:
если тело двигается со скоростью 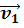 в системе отсчёта
в системе отсчёта 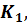 а система отсчёта
а система отсчёта 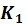 двигается со
скоростью
двигается со
скоростью 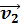 в
системе отсчёта
в
системе отсчёта 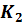 ,
то скорость движения тела, относительно системы
,
то скорость движения тела, относительно системы 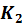 равна:
равна:
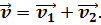
Напомним, что скорость — это векторная величина, поэтому, скорости складываются геометрически.
Пример решения задач.
Лодка двигается по реке с собственной скоростью 8 м/с, так, как показано на рисунке. Скорость течения реки составляет 1 м/с. Определите скорость лодки относительно берега.
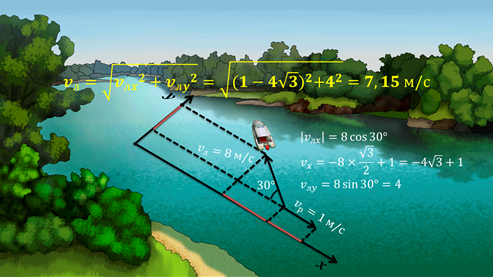
Расположим оси координат
так, чтобы направление оси х совпадало с направлением течения реки.
Тогда проекция скорости на ось х будет равна 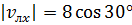 , т.к. на рисунке нам
указан угол между направлением течения и скоростью лодки. Обратите внимание,
что эта проекция будет отрицательной. В этом можно убедиться при построении
проекции, да и чисто логически ясно, что лодка плывет против течения, а значит,
одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения
на ось х, конечно же, будет равна 1 м/с, поскольку направление течение
совпадает с направлением оси х. Тогда скорость движения лодки по оси х
относительно берега равна:
, т.к. на рисунке нам
указан угол между направлением течения и скоростью лодки. Обратите внимание,
что эта проекция будет отрицательной. В этом можно убедиться при построении
проекции, да и чисто логически ясно, что лодка плывет против течения, а значит,
одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения
на ось х, конечно же, будет равна 1 м/с, поскольку направление течение
совпадает с направлением оси х. Тогда скорость движения лодки по оси х
относительно берега равна: 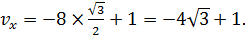
Проекция вектора
скорости лодки на ось у равна 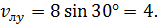
Разумеется, проекция скорости течения на ось у будет равна нулю, потому что вектор скорости течения перпендикулярен этой оси. С помощью геометрической суммы проекций мы можем найти модуль скорости лодки, относительно берега:
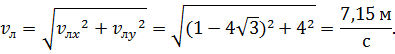
Давайте рассмотрим теперь пример, который научит вас складывать какие угодно скорости.

Найдём скорость машины,
относительно самолёта в заданной системе координат. Сначала найдем проекции
скорости машины на оси х и у. Точно так же, как и в предыдущем
примере, проекция на ось х равна: 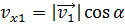 , а проекция на ось у
равна
, а проекция на ось у
равна 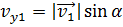 .
Точно так же находим проекции скорости самолёта на координатные оси:
.
Точно так же находим проекции скорости самолёта на координатные оси:
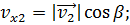
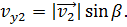
Напомним, что проекции являются скалярными величинами, поэтому их мы складываем алгебраически:
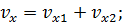
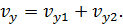
Теперь, когда мы нашли проекции скорости машины относительно самолёта на оси х и у, мы можем найти модуль скорости с помощью геометрической суммы:
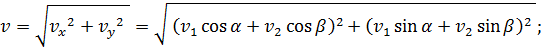
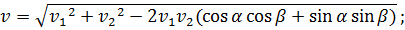
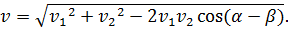
Таким образом, мы получили расчётную формулу для вычисления модуля скорости одного движущегося тела, относительно другого движущегося тела. Эта формула справедлива для тех случаев, когда оба тела двигаются в одной плоскости.
Заметим, что закон сложения скоростей справедлив и для неравномерного движения. В этом случае нужно складывать мгновенные скорости.
Пример решения задачи.
Задача. Мяч катится с постоянной скоростью 10 м/с. Ему наперерез бежит футболист со скоростью 7 м/с, так, как показано на рисунке. Через какое время футболист поймает мяч, если изначально между футболистом и мячом было 40 метров?

Начнём с того, что когда футболист поймает мяч, они будут находиться в одной точке. Расположим систему координат так, чтобы направление движения футболиста совпадало с направлением оси х. Тогда, скорость мяча будет направлена под углом 45о градусов к оси х. Сделаем проекции скорости мяча на оси х и у.



 Получите свидетельство
Получите свидетельство Вход
Вход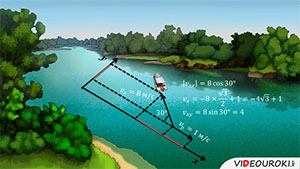



 0
0 22279
22279

