Астрономия — это одна из древнейших и самых увлекательных наук, которая изучает объекты и явления, наблюдаемые во Вселенной. Её истоки относятся к далёкому каменному веку, то есть примерно к шестому — третьему тысячелетию до нашей эры. На протяжении всей своей истории, человечество стремилось понять природу наблюдаемых объектов и явлений, разгадать тайны окружающего мира и определить своё место в нём. Простое созерцание происходящих явлений и их наивное толкование постепенно сменялись попытками научного объяснения причин наблюдаемых явлений. Когда в VI веке до нашей эры в Древней Греции началось бурное развитие философии как науки о природе, астрономические знания стали неотъемлемой частью человеческой культуры.
В настоящее время под астрономией понимается фундаментальная наука, которая изучает строение, движение, происхождение и развитие небесных тел, их систем и всей Вселенной в целом.
На протяжении тысячелетий астрономы изучали положение небесных объектов на звёздном небе и их взаимное перемещение с течением времени. Нам, как и людям в древности, кажется, что все звёзды одинаково удалены от нас и располагаются на некой сферической поверхности неба — небесной сфере, — которая как единое целое вращается вокруг Земли.

Под небесной сферой мы с вами будем понимать воображаемую сферу произвольного радиуса, центр которой в зависимости от решаемой задачи совмещают с той или иной точкой пространства.
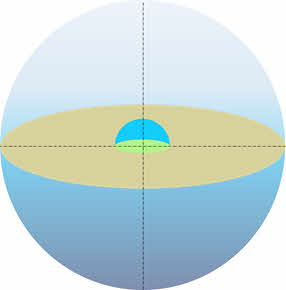
Например, центр небесной сферы может быть выбран в месте наблюдения (глаз наблюдателя), в центре Земли или Солнца и так далее. Важно понимать, что на поверхности небесной сферы располагаются не сами звёзды, а их проекции.
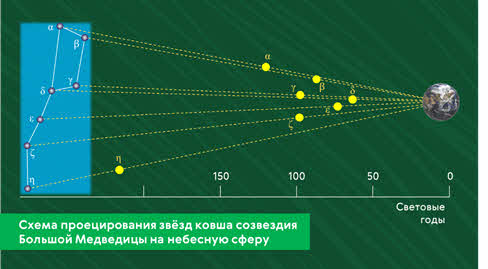
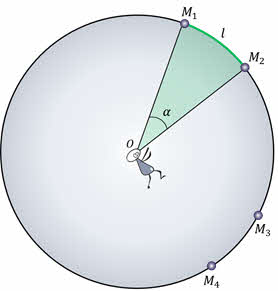
Расстояния между звёздами на небесной сфере можно выражать только в угловой мере. Эти угловые расстояния измеряются величиной центрального угла между лучами, направленными на одну и на вторую звезду, или же эти расстояния можно вычислить по длине соответствующей дуги между звёздами на поверхности небесной сферы.
Прямая, проходящая через центр небесной сферы и совпадающая с направлением нити отвеса в месте наблюдения, называется отвесной или вертикальной линией. Как видим, эта линия пересекает небесную сферу в двух диаметрально противоположных точках. Верхняя точка называется зенитом, нижняя — нади́ром.
Если через центр небесной сферы провести плоскость, перпендикулярную отвесной линии, то мы получим плоскость истинного или математического горизонта.
Большой круг небесной сферы, проходящий через зенит, светило и надир, называется кругом высоты или вертикальным кругом.
А прямая, проходящая через центр небесной сферы параллельно оси вращения Земли, называется осью мира. Она тоже пересекает небесную сферу в двух диаметрально противоположных точках. Точка, вблизи которой находится Полярная звезда, называется Северным полюсом мира, а противоположная ей точка — Южным полюсом мира.
Проведя через центр небесной сферы перпендикулярно оси мира большой круг, мы получим небесный экватор. Он, наподобие земного экватора, делит небесную сферу на две части: Северное полушарие и Южное.
Если провести большой круг через полюсы мира и светило, то мы получим круг склонения светила.
Большой круг небесной сферы, проходящий через точки зенита, надира и полюсы мира, называется небесным меридианом. Он пересекается с истинным горизонтом в двух диаметрально противоположных точках. Точка, которая находится ближе к Северному полюсу мира, называется точкой севера. Соответственно, та точка, которая находится ближе к Южному полюсу мира, называется точкой юга.
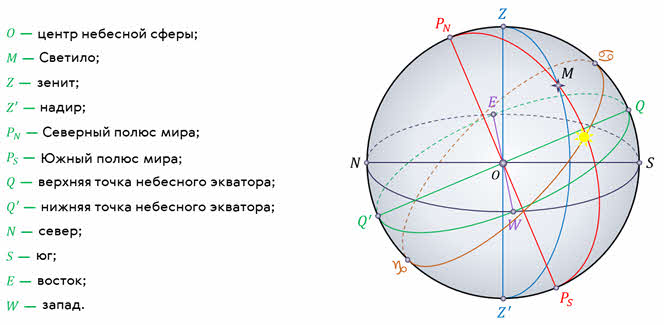
Если мы соединим эти две точки, то получим так называемую полуденную линию, по направлению которой падают тени от предметов в полдень.
С небесным экватором истинный горизонт также пересекается в двух диаметрально противоположных точках — точке востока и точке запада.
Помимо этого, на небесной сфере принято указывать и видимый годовой путь Солнца среди звёзд. Он называется эклиптикой. Эклиптика наклонена к небесному экватору под углом 23о27' и пересекает его в двух точках — точках весеннего и осеннего равноденствий.
Положение светил на небе определяется по отношению к точкам и кругам небесной сферы. Для этого были введены небесные координаты. В астрономии применяется несколько систем координат. Мы же с вами познакомимся только с одной из них — экваториальной системой координат, аналогичной той, которая используется в географии. В этой системе координат основным кругом небесной сферы является небесный экватор. А координатами служат склонение и прямое восхождение.
Склонение светила — это угловое расстояние светила от небесного экватора, измеренное вдоль круга склонения. Обозначается склонение малой греческой буквой δ и оно аналогично географической широте. У светил, расположенных к северу от экватора, склонение считается положительным, а расположенных к югу от экватора — отрицательным. При этом за начальную точку отсчёта склонения на небесном экваторе принимается точка весеннего равноденствия.
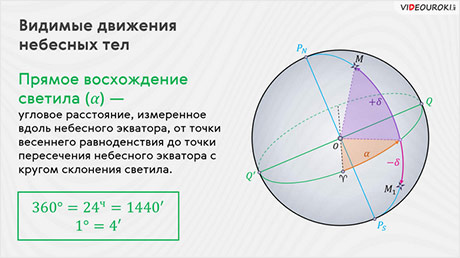
Вторая координата — прямое восхождение — указывает положение светила на небе. То есть это угловое расстояние, измеренное вдоль небесного экватора, от точки весеннего равноденствия до точки пересечения небесного экватора с кругом склонения светила.
Обозначается склонение малой греческой буквой α. А отсчитывается оно в сторону, противоположную суточному вращению небесной сферы, в пределах от 0о до 360о градусов или от 0 до 24 часов. Хотя в астрономии склонение принято выражать не в градусной мере, а в часовой.
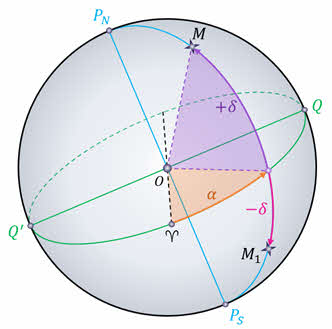
В экваториальной системе координаты звёзд не связаны с суточным движением небесной сферы и изменяются очень медленно, так как достаточно далеки от нас. Поэтому именно эта система координат применяется для составления звёздных глобусов, карт и каталогов.
Звёздные карты представляют собой проекции небесной сферы на плоскость с нанесёнными на неё объектами в определённой системе координат.
Давайте остановимся и рассмотрим карту звёздного неба поподробнее. Итак, в центре нашей звёздной карты располагается северный полюс мира. Рядом с ним Полярная звезда. Сетка экваториальных координат представлена на карте радиально расходящимися от центра лучами и концентрическими окружностями. На краю карты, возле каждого луча, написаны числа, обозначающие прямое восхождение.
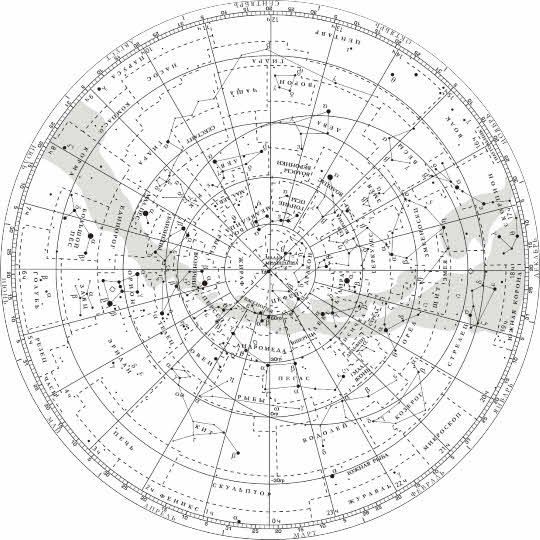
Луч, от которого начинается отсчёт прямого восхождения, проходит через точку весеннего равноденствия, обозначенную на карте символом овна. Склонение отсчитывается по этим лучам от окружности, которая изображает небесный экватор и имеет обозначение 0о. Звёзды изображают на карте кружками различного диаметра (в зависимости от звёздной величины). Те из них, которые образуют характерные фигуры созвездий, соединены сплошными линиями. А границы созвездий обозначены пунктиром.
С помощью карты нетрудно определить координаты интересующей звезды. Так, например, склонение звезды Сириус примерно –16о, а её прямое восхождение — 6h 45m.
Вы наверняка знаете, что в течение практически 19 веков в астрономии господствовала геоцентрическая система мироустройства Клавдия Птолемея, в которой планета Земля находилась в центре всего мироздания. А все остальные небесные тела, в том числе и Солнце, вращались вокруг неё.

И лишь в середине XVI века вышел великий труд Николая Коперника «Об обращении небесных сфер», в котором приводились доводы о том, что центром нашей системы является не Земля, а Солнце. Так возникло гелиоцентрическое учение, которое дало ключ к познанию Вселенной.

Интересно, что доказать теорию Коперника с помощью прямых наблюдений удалось лишь во второй половине XIX века, когда учёные научились определять параллактическое смещение далёких звёзд. Параллактическим смещением называется периодическое смещение звезды на фоне более далёких звёзд. Как удалось установить, кажущееся перемещение более близкой звезды на фоне очень далёких звёзд происходит по эллипсу с периодом в один год и отражает движение наблюдателя вместе с Землёй вокруг Солнца. Этот небольшой эллипс, который описывает звезда, называется параллактическим эллипсом.

В угловой мере его большая полуось равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом и обозначается греческой буквой π или латинской буквой р.
Зная годичное параллактическое смещение звезды, можно легко определить расстояние до неё:
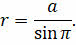
В записанной формуле а — это средний радиус земной орбиты (её большая полуось) (≈ 150 млн км). Для простоты вычислений, величину большой полуоси орбиты Земли приняли равной одной астрономической единице (1 а. е.). Эта единица измерения стала основой для вычисления всех остальных расстояний в Солнечной системе.
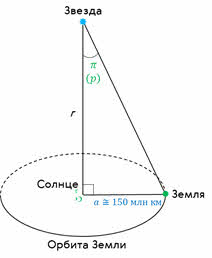
Если учесть, что годичные параллаксы звёзд измеряются десятитысячными долями секунды, а большая полуось земной орбиты равна одной астрономической единице, то можно получить формулу для вычисления расстояния до звезды в астрономических единицах:
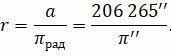
В России первые измерения годичного параллакса были проведены Василием Яковлевичем Струве для самой яркой звезды Северного полушария Веги.

А по этим данным смогли оценить расстояние до этой звезды. Оно оказалось равным примерно 1 676 951 а. е. Согласитесь, что для измерения расстояний до звёзд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звёзд в астрономии применяется специальная единица длины — парсек, название которой происходит от двух слов — «параллакс» и «секунда».
Парсек — это расстояние, с которого средний радиус земной орбиты, перпендикулярный лучу зрения, виден под углом в одну угловую секунду:
1 пк = 206 265 а. е. =30,8586 трлн км.
Исходя из определения, расстояние в парсеках равно обратной величине годичного параллакса:
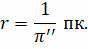
В начале XVII века австрийский астроном Иоганн Кеплер открыл кинематические законы движения планет. В своих поисках он исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Кеплер пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников и так далее. Но лишь переехав в Прагу и став учеником датского астронома Тихо Браге, Кеплер натолкнулся на идеи, по-настоящему обессмертившие его имя в анналах науки.
Изучая движение Марса в пространстве, а также воспользовавшись многолетними определениями координат и конфигураций этой планеты, проведёнными Тихо Браге, Кеплеру удалось сформулировать свои первые два закона движения планет. Первый закон Кеплера звучит так: все планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце.
Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется его большой осью. А отрезок, проходящий через центр эллипса перпендикулярно большой оси, называется малой осью эллипса.
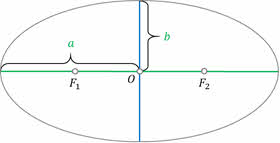
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях, называются, соответственно, большой полуосью и малой полуосью эллипса.
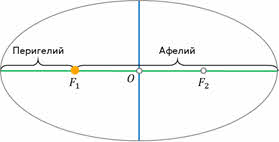
Предположим, что Солнце расположено в фокусе F1. Тогда ближайшая к Солнцу точка орбиты планеты называется перигелием. А наиболее удалённая от Солнца точка — афелием.
Учёный также обратил внимание на то, что положение Марса на траектории не является равномерным. Это указывало на то, что скорость Марса по орбите меняется: она принимает максимальное значение в перигелии и минимальное — в афелии. Но самое интересное, что при этом радиус-вектор планеты за равные промежутки времени описывает равновеликие площади. Обнаруженная закономерность впоследствии получила название второго закона Кеплера, которую иногда называют законом площадей).
Интересно, что первый и второй законы были опубликованы Кеплером в 1609 году в книге «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс». Хотя реально первый закон Кеплера был открыт в 1605 году, а второй — в 1602.
Свой третий закон Кеплер сформулировал лишь в 1618 году. Он гласит, что квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит:
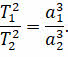
Третий закон Кеплера заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя уже известные их периоды обращения вокруг него.
Строгое математическое доказательство законов Кеплера было получено лишь после того, как Ньютоном были открыты закон Всемирного тяготения и закон сохранения момента импульса — второй закон Ньютона. Более того, закон всемирного тяготения смог расширить законы движения планет. В частности, Ньютону удалось показать, что движение одного небесного тела в поле тяготения другого небесного тела происходит по одному из конических сечений: окружности, эллипсу, параболе или гиперболе.
Формулировка второго закона не потребовала обобщений. А вот третий закон Кеплера стал звучать так: квадраты сидерических периодов спутников, умноженные на сумму масс главного тела и спутника, относятся как кубы больших полуосей орбит спутников:
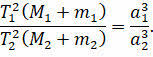
С помощью третьего обобщённого закона Кеплера стало возможным вычислять массы любых планет, имеющих спутники.

 Получите свидетельство
Получите свидетельство Вход
Вход




 6008
6008

