Закон радиоактивного распада

Серия экспериментов, проведённая с соля́ми урана в период 1899—1900 гг., показала, что радиоактивное излучение в сильном магнитном поле распадается на три составляющие:

лучи первого типа отклоняются так же, как поток положительно заряженных частиц. Их назвали альфа-лучами;

лучи второго типа обычно отклоняются в магнитном поле так же, как поток отрицательно заряженных частиц, их назвали бета-лучами (существуют, однако, позитронные бета-лучи, отклоняющиеся в противоположную сторону);

а лучи третьего типа, которые не отклоняются магнитным полем, назвали гамма-излучением.

Хотя в ходе исследований были обнаружены и другие типы частиц, испускающихся при радиоактивном распаде, эти названия сохранились до сих пор, поскольку соответствующие типы распадов наиболее распространены.

Позже было установлено, что альфа-лучи представляют собой поток ядер атома гелия. А продуктом распада материнского ядра оказывается элемент, зарядовое число которого на две единицы меньше, а массовое число на четыре единицы меньше, чем у материнского ядра:

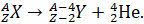
При бета-минус-распаде ядро атома испускает один электрон и антинейтрино, в результате чего образуется ядро нового элемента с тем же самым массовым числом, но с атомным номером на единицу больше, чем у материнского ядра:

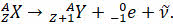
А при бета-плюс-распаде ядра самопроизвольно испускают позитрон и электронное нейтрино. Ядро нового химического элемента имеет то же самое массовое число, но его атомный номер уменьшается на единицу:

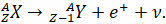
Исследование изотопов различных химических элементов показало, что большинство из них превращается в более устойчивые изотопы путём радиоактивного распада. При этом очевидно, что в процессе радиоактивного распада число ядер со временем уменьшается. Но предсказать, когда именно распадётся то или иное ядро, оказалось невозможным. Однако было установлено, что для каждого радиоактивного ядра существует некоторое характерное время, называемое периодом полураспада, спустя которое в исходном состоянии остаётся половина первоначального количества радиоактивных ядер. При этом распавшиеся ядра превращаются в ядра других, более устойчивых изотопов.

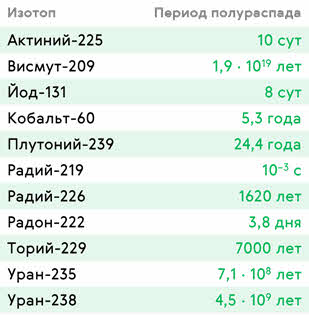
Период полураспада характеризует такое свойство, как активность радионуклида. Данная величина указывает на интенсивность радиоактивных превращений, т. е. на количество радиоактивных распадов атомных ядер, происходящих за единицу времени.

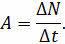
В СИ единицей активности является беккерель. 1 Бк — это активность радиоактивного препарата, в котором происходит распад одного ядра за одну секунду. Внесистемной единицей активности служит кюри (1 Ки = 3,7 · 10¹⁰ Бк).

Таким образом, чем меньше период полураспада радионуклида, тем быстрее происходит его распад и тем активнее элемент.

Отметим также, что период полураспада не зависит от того, в каком состоянии находится вещество: твёрдом, жидком или газообразном. Кроме того, период полураспада не зависит от времени, места и условий, в которых находится радиоактивное вещество. Поэтому количество радиоактивных ядер «тогда», и «сейчас» зависит только от промежутка времени, прошедшего с момента начала регистрации процесса распада ядер.

Как мы говорили, точно предсказать, когда произойдёт распад данного ядра невозможно. Однако можно оценить среднее число ядер, которые распадутся за данный промежуток времени. Закон, который описывает интенсивность радиоактивного распада от времени и количества радиоактивных атомов в образце, был открыт Фредериком Содди и Эрнестом Резерфордом в 1903 году. В своих работах «Сравнительное изучение радиоактивности радия и тория» и «Радиоактивные превращения» они сформулировали закон радиоактивного распада следующим образом: «Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии».

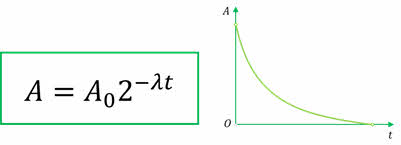
Давайте с вами получим математическую форму закона радиоактивного распада. Для этого будем считать, что в начальный момент времени число радиоактивных ядер составляло «Эн нулевое». Тогда, через промежуток времени, равный периоду полураспада, у нас останется? Правильно, половина от их первоначального количества.

За второй период полураспада у нас распадётся половина от половины исходного числа ядер. То есть нераспавшимися останется четверть от начального числа ядер. Рассуждая далее аналогичным образом, найдём, что за промежуток времени, равный n периодам полураспада, радиоактивных ядер останется:

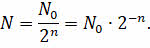
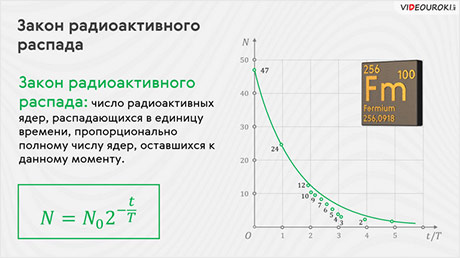
Поскольку n — это отношение времени наблюдения к периоду полураспада радиоактивного элемента, то последнюю запись можно представить в том виде, который вы сейчас видите на экране:

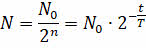
Полученное соотношение и выражает математическую запись закона радиоактивного распада. С его помощью можно найти число нераспавшихся ядер в любой момент времени.

Для примера давайте с вами решим такую задачу. Изотоп 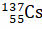 является β^–-радиоактивным с периодом полураспада 30 лет. Определите заряд β-частиц, испущенных этим изотопом за 15 лет, если масса исходного препарата равна 2 г.

Отметим, что закон радиоактивного распада является статистическим, так как он справедлив до тех пор, пока число нераспавшихся ядер остаётся достаточно большим.

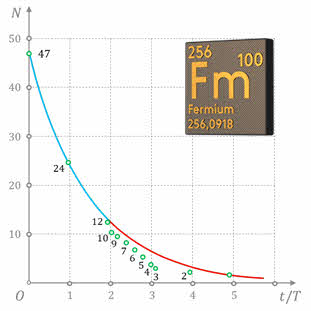
Вы видите теоретический и экспериментальный графики распада 47 ядер изотопа фермия-256, период полураспада которого равен 3,5 часам. Из графиков хорошо видно, что пока ядер было достаточно много (от 47 до 12), показательная функция хорошо описывала закон распада. Однако при меньшем числе ядер истинная зависимость существенно отличается от показательной функции.

Теперь давайте с вами выясним, от чего же зависит активность радионуклида. Для этого вспомним, что в процессе радиоактивного распада количество нераспавшихся ядер уменьшается, значит, активность образца равна скорости уменьшения количества нераспавшихся ядер:

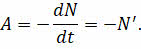
Подставим в данное уравнение математическую запись закона радиоактивного распада и возьмём первую производную по времени полученного выражения.

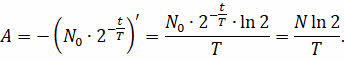
После всех математических преобразований получим, что активность источника прямо пропорциональна числу радиоактивных ядер, имеющихся в образце в данный момент времени, и обратно пропорциональна периоду полураспада данного радиоактивного вещества.

Представим полученную нами формулу в том виде, как это показано на экране:

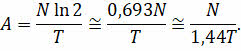
Произведение, стоящее в знаменателе формулы представляет собой среднее время жизни радиоактивного изотопа. Оно также равно периоду, за который количество нераспавшихся ядер уменьшается в е ≅ 2,72 раз.

Как вы уже знаете, все радиоактивные ядра данного изотопа одинаковы. Поэтому и вероятность распада для каждого из них одинакова в каждую секунду. То есть распад ядра — это, так сказать, не «смерть от старости», а скорее «несчастный случай» в его жизни. Ядро может распасться сейчас, а может прожить в образце неопределённо долго без распада.

Вероятность распада одного ядра данного изотопа за одну секунду называется постоянной распада и обозначается греческой буквой лямбда (λ). Для любого ядра данного изотопа постоянная распада одинакова. Но для ядер различных изотопов постоянная распада различна.

Давайте предположим, что в некотором радиоактивном образце имеется N ядер. Тогда вероятность распада равна той части ядер (|dN/N|) образца, которая распадётся за единицу времени:

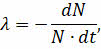
(знак «–» в уравнении указывает на убывание числа радиоактивных ядер данного изотопа с течением времени). Из этой формулы следует, что доля распавшихся ядер равна произведению постоянной распада на малый промежуток времени, за который они распались:

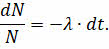
Проинтегрируем это выражение от начального до произвольного момента времени:

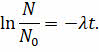
Воспользовавшись свойствами логарифма, мы с вами получим второй вариант записи закона радиоактивного распада:

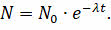
На основании полученного уравнения мы с вами можем определить, от чего зависит постоянная радиоактивного распада. Итак, предположим, что время наблюдения за радиоактивным препаратом равно его периоду полураспада. Значит, через этот промежуток времени в образце останется половина от первоначального количества ядер:

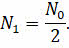
Перепишем закон радиоактивного распада с учётом этого выражения.

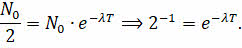
И прологарифмируем полученное равенство по основанию «Е».

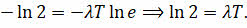
Из полученной записи видно, что постоянная распада обратно пропорциональна периоду полураспада радиоактивного элемента:

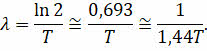
Сравнивая эти формулы с формулой, полученной нами ранее для активности вещества, видим, что активность образца равна произведению постоянной распада и числа радиоактивных ядер в образце в данный момент: