Уравнение РПД

Мы знаем, что в каждый момент времени, положение точки задаётся радиус-вектором. Пусть в момент времени t₀, начальное положение точки задаёт радиус-вектор 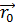. Во все последующие моменты времени положение точки будет описываться радиус-вектором .

Исходя из определения скорости равномерного прямолинейного движения, запишем:

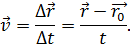
Как правило, начальный момент времени — это точка отсчёта, поэтому примем t₀ = 0. Если мы теперь выразим 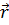 из полученного выражения, то получим функцию зависимости радиус-вектора от времени:

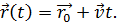
Это и есть уравнение равномерного прямолинейного движения. То есть, если нам известно начальное положение точки и скорость её движения, то мы сможем найти радиус-вектор в каждый момент времени.

Вместо векторного уравнения можно использовать уравнение для каждой из координат:

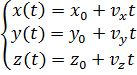
Поскольку пройденный путь — это изменение координаты х в данном случае, мы можем найти его, используя модуль скорости. Заметим, что числовые значения пройденного пути и перемещения будут совпадать при прямолинейном движении. Только не стоит забывать, что пройденный путь — это скалярная величина, которая не может быть отрицательной.

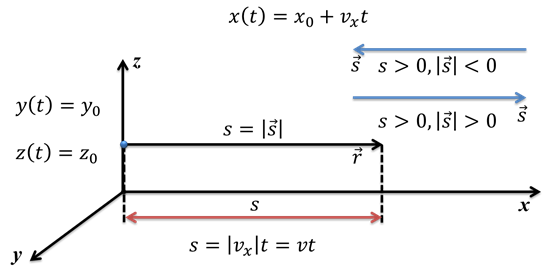
Перемещение же, легко может быть отрицательным, если точка двигается в направлении, противоположном направлению координатной оси.

Итак, мы выяснили, что для описания равномерного прямолинейного движения достаточно получить уравнение для одной координаты. Давайте рассмотрим, как будут выглядеть графики функций зависимости скорости и координаты от времени. Начнём с простого: при равномерном движении скорость постоянна. Поэтому график зависимости скорости от времени будет представлять собой прямую горизонтальную линию.

Иными словами, при равномерном движении скорость не зависит от времени, так как является константой. Заметим, что если мы рассмотрим конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением координаты х. Действительно, ведь длина одной из сторон прямоугольника — это скорость, а длина другой — это время.

Рассмотрим теперь несколько графиков зависимости координаты от времени. На рисунке вы видите три прямых, каждая из которых описывается одним и тем же уравнением.

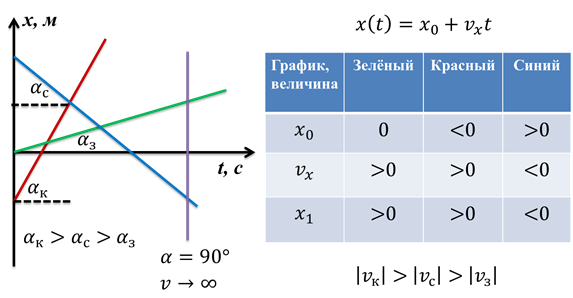
Точки пересечения этих графиков с осью х соответствуют значениям начального положения х₀. Как видно из графика, для зелёной прямой х₀ = 0, для синей прямой х₀ > 0, а для красной — х₀ < 0. На графике видно, что скорость для красной и зелёной прямых больше нуля. Действительно, ведь значение координаты х увеличивается с течением времени. Значит, тело двигается в направлении, совпадающем с направлением оси х. Это соответствует положительному перемещению, а, значит, положительной скорости. В случае с синей прямой, мы видим противоположную картину: значит, тело двигается в обратном направлении, поэтому скорость отрицательная. Из графика также видно, что конечная координата для синей прямой будет отрицательной, а для красной и зелёной прямых — положительной. И ещё, исходя из графиков, мы можем судить о модуле скорости. Очевидно, что тело, движение которого описано красной прямой двигается быстрее остальных. Ведь за тот же промежуток времени оно проходит большее расстояние. Используя этот же аргумент, можно сказать, что для синей прямой модуль скорости больше, чем для зелёной. Из этих наблюдений можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем больше скорость движения. Действительно: представьте на минуту график зависимости координаты от времени, который представляет собой вертикальную прямую. Это будет означать, что скорость бесконечно большая, т.к. тело перемещается на любое расстояние за промежуток времени, равный нулю. Разумеется, в классической механике такие перемещения невозможны.

Примеры решения задач.

Задача 1. Точка, равномерно двигаясь вдоль оси X, переместилась из координаты  в координату за 5 с. Определите модуль и направление скорости этой точки.

Задача 2. Две машины равномерно двигаются по одной прямой. Опишите условия, при которых столкновение невозможно.

Движения и того, и другого автомобиля описываются одним и тем же общим уравнением. Обозначим одну машину за грузовик, а другую за легковую. На графике обозначим грузовик синей точкой, а легковую машину — красной точкой. Итак, рассмотрим первый случай: машины двигаются в разные стороны. Тогда, скорость одной машины должна быть положительной, а скорость другой — отрицательной (например, легковая машина будет двигаться в положительном направлении). Чтобы машины не столкнулись, начальная координата машины с отрицательной скоростью, должна быть меньше, чем начальная координата машины с положительной скоростью. В противном случае, они будут двигаться навстречу друг другу и столкнуться. Графически это можно изобразить так:

Скорость красного графика положительная, поскольку координата х увеличивается с течением времени, а скорость синего графика — отрицательная, поскольку координата х уменьшается с течением времени. Эти графики никогда не пересекутся, поэтому столкновения не произойдёт. Заметим, что при таком раскладе, скорости не имеют значения. Имеет значение только знак (то есть направление движения). Конечно, вы можете сказать, что если мы продолжим графики, то они всё же пересекутся. Но для этого машинам нужно переместиться в прошлое, потому что координата времени, соответствующая точке пересечения, отрицательная.

Рассмотрим теперь второй случай: когда машины двигаются в одном направлении, и при этом, машина, идущая впереди, едет быстрее. Что значит, машина, идущая впереди? Это значит, что её начальная координата должна быть больше.

То есть условие таково: машина, начальная координата которой больше, должна двигаться со скоростью не меньше, чем скорость второй машины. Опять же, если мы изобразим это графически, то увидим, что графики не пересекаются.

Начальная координата красного графика больше и скорость тоже больше. Если же скорости будут одинаковы, то это будет означать одинаковый наклон синей и красной линий по отношению к оси времени. В этом случае, графики будут представлять собой параллельные прямые, а такие прямые, как известно, не пересекаются.