Равноускоренное прямолинейное движение. Ускорение

Данная тема посвящена равноускоренному прямолинейному движению и ускорению.

В прошлой теме рассматривался самый простой вид механического движения — равномерное прямолинейное движение.

Равномерное движение — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, то есть это движение с постоянной по модулю и направлению скоростью.

То есть, такое движение – это идеализированный пример. На самом же деле движение тел в обычных условиях, как правило, неравномерное. Примером может послужить движение человека, вышедшего на прогулку. В начале движения он бодр, весел и полон сил. Но со временем мышцы тела начинают уставать, движение человека замедляется до тех пор, пока он окончательно не устанет и не присядет отдохнуть. Такой вид движение в физике назвали неравномерным. И так, неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения, или, говорят, меняется проекция вектора скорости.

При этом тело может менять свою скорость быстро или медленно. Например, мяч, катящийся по земле, плавно снижает свою скорость, пока полностью не остановится. Однако если бросить этот мяч в стену, то при ударе, он изменит свою скорость мгновенно. Для того, чтобы описать насколько быстро меняется скорость тела, в физике ввели величину, которую назвали ускорением тела.

Сейчас понятие «ускорение» является чем-то обыденным. Однако широкое использование ускорения в работах по механике началось лишь после выхода в свет в 1851 году сочинения «Элементы механики» француза Анри Эме Резаля: «Подобно тому, как скорость определяет быстроту изменения положения тела, ускорение определяет насколько быстро меняется скорость тела».

Таким образом, ускорение — это физическая величина, равная отношению изменения скорости к промежутку времени, в течении которого это изменение произошло. Разумеется, ускорение, как и скорость, является векторной величиной.

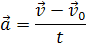
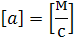
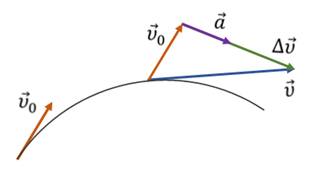
Напомним, что в кинематике вектор ускорения направлен параллельно вектору изменения скорости тела в сторону вогнутости траектории.

Единицей измерения ускорения в системе СИ является метр, деленный на секунду в квадрате.

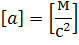
Физический смысл этой единицы измерения можно объяснить так: модуль ускорения показывает, на сколько метров в секунду изменилась скорость тела за одну секунду. Например, если ускорение равно 3 м/с², то это означает, что ежесекундно скорость увеличивается на 3 м/с.

Для простоты дальнейших рассуждений будем рассматривать самый простой вид движения с ускорением — равноускоренное прямолинейное движение тела, то есть такое движение, при котором его скорость за любые равные промежутки времени изменяется одинаково. Так же говорят, что это движение с постоянным по модулю и направлению ускорением.

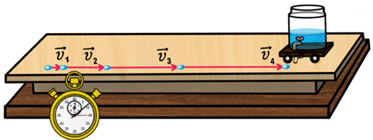
Основная задача кинематики состоит в том, чтобы найти положение тела в любой момент времени. Для того, чтобы ее решить, нужно сначала суметь найти скорость тела в любой момент времени. Для этого следует знать закон, по которому происходит изменение мгновенной скорости от времени для равноускоренного движения. Здесь все просто, достаточно выразить вектор скорости из формулы определения ускорения тела, воспользовавшись известными математическими приемами.

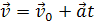
Полученное уравнение называется уравнением скорости для равноускоренного движения. Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя, поэтому перепишем уравнение в проекции на ось х.

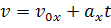
Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.

Как и в случае равномерного прямолинейного движения тела, зависимости кинематических величин от времени при равноускоренном движении можно изобразить графически. Для начала нарисуем графики зависимости ускорений для трех тел от времени.

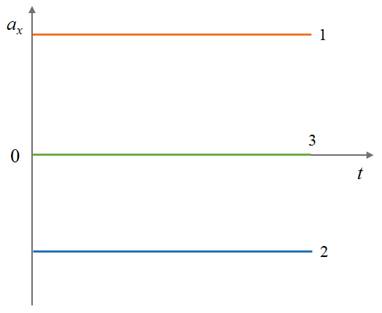
Так как в случае равноускоренного движения модуль и направление вектора ускорения не меняется, то график ускорения имеет вид прямой, параллельной оси времени.

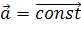
При этом график располагается над осью времени, если тело движется равноускорено; под осью времени — в случае равнозамедленного движения (то есть когда проекция ускорения на координатную ось меньше нуля); и будет совпадать с осью времени, если тело движется прямолинейно и равномерно.

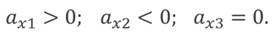
Теперь изобразим графики зависимости скорости от времени. Известно, что при равноускоренном движении скорость с течением времени не остается постоянной, а меняется со временем. При этом, как видно из уравнения, зависимость скорости от времени является линейной функцией и поэтому график скорости имеет вид прямой, наклоненной к оси времени. Причем, чем больше угол наклона, тем большее ускорение имеет тело.

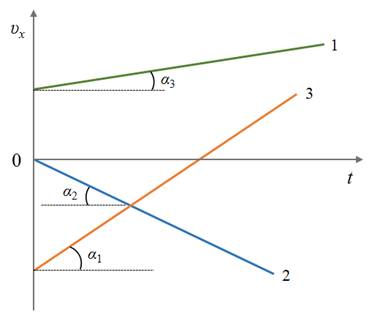
На графике прямая 1 соответствует движению с положительным ускорением и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением без начальной скорости, а прямая 3 — движению тела с положительным ускорением и отрицательной начальной скоростью.

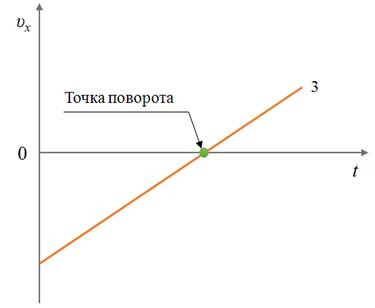
Рассмотрим подробнее график скорости для тела 3. Что можно сказать про эту точку? Какие изменения происходят с движением тела в ней? В этой точке скорость тела меняет свое направление на противоположное. Такая точка называется точкой поворота.

Теперь рассмотрим, как определить местоположение тела при равноускоренном движении, то есть как можно определить координату тела, путь и перемещение при таком движении.

Первым, кто решил задачу о местоположении тела в определенный момент времени при равноускоренном движении, был итальянский учёный Галилео Галилей. Для своих опытов он использовал наклонную плоскость с гладкой канавкой посередине, по которой скатывались латунные шары. По водным часам он засекал определённый интервал времени и фиксировал расстояния, которые за это время преодолевали шары. Таким образом, Галилей выяснил, что это расстояние квадратично зависит от времени движения шаров.

Получим формулу для определения перемещения при равноускоренном движении графическим методом. Для этого обратимся к графику зависимости скорости тела от времени при равноускоренном движении.

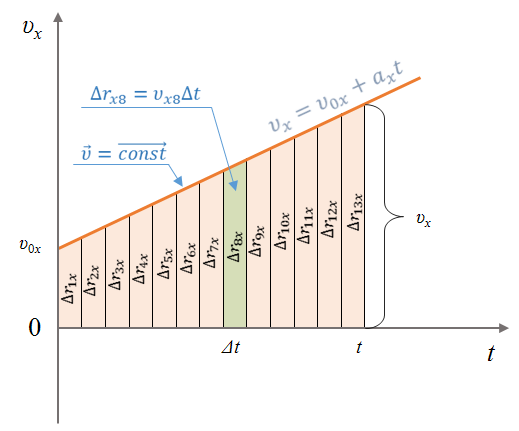
Разобьем график скорости на такие бесконечно малые прямоугольные участки, чтобы на них скорость тела можно было считать постоянной. Тогда перемещение за бесконечно малый промежуток времени будет равно площади закрашенной полоски. Найдя суммарную площадь всех малых фигур на выбранном интервале времени, а она будет равна площади трапеции, можно определить перемещение тела

Данное уравнение называется уравнением перемещения при равноускоренном движении в проекциях на координатную ось.

Так как рассматриваем прямолинейное движение, то в случае, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда определяется модуль перемещения, то определяется и пройденный путь. Заменив проекции соответствующими векторами, получим уравнение перемещения в векторном виде

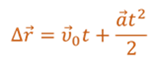
Учитывая, что проекция перемещения равна разности между конечной и начальной координатой тела, преобразуем уравнение перемещения в проекциях на координатную ось

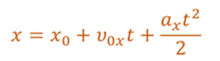
Полученное равенство носит название – основное кинематическое уравнение равноускоренного движения.

Рассмотрим некоторые важные зависимости между величинами равноускоренного прямолинейного движения.

Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Следовательно, пути, пройденные телом за 1, 2, 3, 4 и так далее секунды будут относиться как квадраты последовательных натуральных чисел

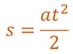
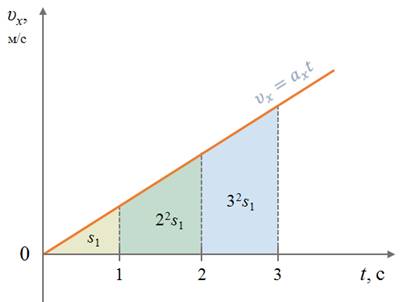
s₁ : s₂ : s₃ = 1 : 2² : 3²

И еще одна важная зависимость: для любого равноускоренного движения, пути, пройденные телом за любые равные промежутки времени, будут относиться как последовательный ряд нечетных чисел

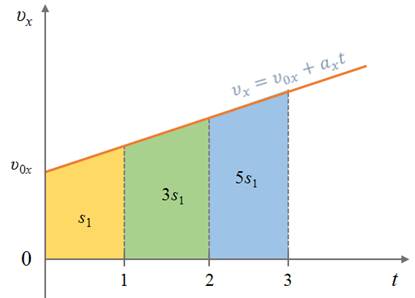
s_1-ю : s_2-ю : s_3-ю = 1 : 3 : 5

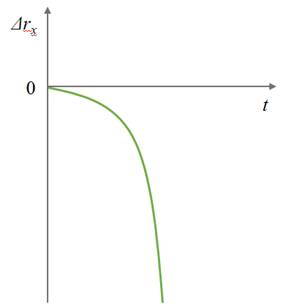
Рассмотрим, как графически можно изобразить зависимость проекции перемещения от времени при равноускоренном движении. Так как проекция перемещения квадратично зависит от времени, то графиком перемещения для равноускоренного движения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения тела.

Так на первом графике ускорение тела меньше нуля, начальная скорость равна нулю.

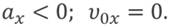
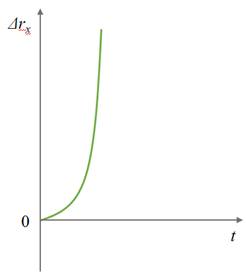
Для второго графика — ускорение и начальная скорость тела больше нуля.

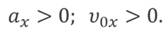
Для третьего — ускорение больше нуля, начальная скорость меньше нуля.

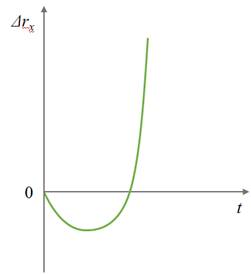
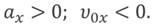
На следующем графике начальная скорость и ускорение тела меньше нуля.

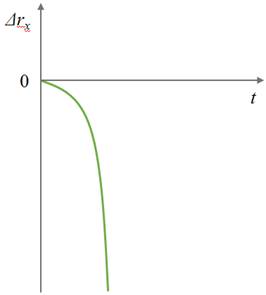
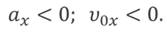
На следующем графике ускорение тела больше нуля, а начальная скорость равна нулю.

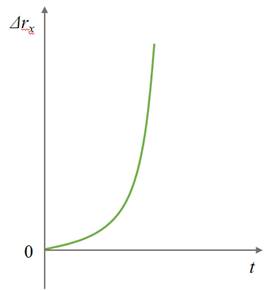
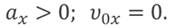
На последнем графике тело двигается замедленно с некоторой начальной скоростью.

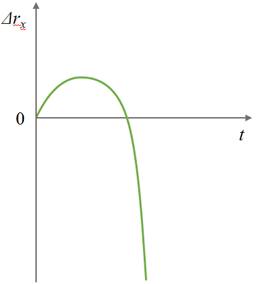
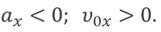
Здесь стоит обратить внимание на то, что для равноускоренного движения графиком движения (то есть графиком зависимости координаты тела от времени), тоже является парабола, положение вершины которой, как и в случае с перемещением, так же зависит от направлений начальной скорости и ускорения тела.

Основные выводы:

Повторили понятие ускорения. Вспомнили, какое движение называется равноускоренным. Вспомнили формулы для определения скорости тела, его координаты, пути и перемещения при равноускоренном движении. А также рассмотрели графическое изображение зависимости кинематических величин от времени при таком движении.