Работа электрического тока

Мы уже знаем, как рассчитать работу электрического тока. Она численно равна произведению напряжения и количества заряда:

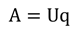
Если мы подставим вместо количества заряда произведение силы тока и времени, то получим формулу, которой тоже уже неоднократно пользовались:

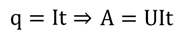
Но теперь, в соответствии с нашими новыми знаниями, мы можем внести некоторые дополнения в данную тему. Используя закон Ома, мы можем получить ещё два выражения, соответствующие работе электрического тока:

Например, эти выражения удобнее использовать, если речь идёт о работе тока, при прохождении через резистор. Кроме того, эти две формулы полезны в тех случаях, когда сопротивление известно, но у нас нет вольтметра или амперметра (в первой формуле не требуется знать напряжение, а во второй — силу тока).

Пример решения задач.

Задача 1. Сила тока в электродвигателе составляет 10 А, а напряжение 200 В. Какую работу совершит такой двигатель за полчаса, если его коэффициент полезного действия составляет 70%?

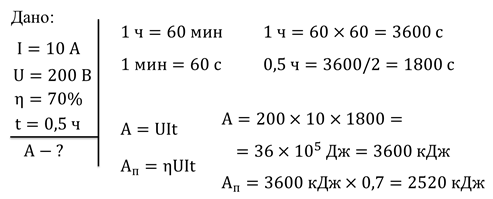
Задача 2. У нас есть две лампочки с одинаковым сопротивлением. При каком подключении к одному и тому же источнику лампочки будут гореть ярче? При каком подключении ток совершит больше работы?

На первый взгляд может показаться, что в задаче не достаточно данных. Но если мы внимательно прочтем условие, то увидим, что данных там вполне достаточно. Во-первых, нам дано, что сопротивление лампочек одинаково. А во-вторых, используется один и тот же источник, значит, напряжение постоянно.

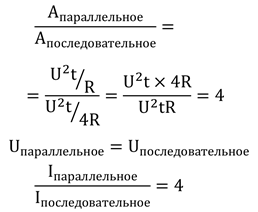
Задача 3. Мы уже упоминали, что слишком большая работа тока не всегда полезна, поскольку это может вызвать перегрев проводов. Напряжение на источнике составляет 5 В. Известно, что лампочка перегорает при совершении работы более 750 Дж/мин, а несущий провод начинает перегреваться при силе тока в 10 А. Исходя из этих данных, какое минимальное сопротивление должно быть у лампочек и сколько максимум лампочек можно подключить при этом сопротивлении?