Поле точечного заряда и заряженного шара. Принцип суперпозиции полей

Вам известно, что электрическое поле не действует на наши органы чувств, его невозможно увидеть. Но мы можем получить некоторое представление о распределении поля в пространстве. Для этого давайте изобразим векторы напряжённости поля, создаваемого неподвижным зарядом, в нескольких точках пространства.

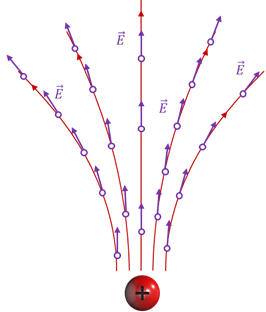
Впервые этот способ изображения электрических полей в виде воображаемых линий, называемых линиями напряжённости (или силовыми линиями), был предложен в 1845 году Майклом Фарадеем.

Под линиями напряжённости мы с вами будем понимать воображаемые направленные линии, касательные к которым в каждой точке поля совпадают по направлению с напряжённостью электрического поля в той же точке.

Интересно, но сам Фарадей считал, что силовые линии существуют в действительности и похожи на растянутые упругие нити. Сейчас же мы точно знаем, что они не более реальны, чем земные меридианы и параллели, изображаемые на глобусах.

При построении линий напряжённости необходимо придерживаться следующих правил. Во-первых, касательная к линии напряжённости в каждой точке должна совпадать с направлением вектора напряжённости.

Во-вторых, следует помнить, что линии напряжённости электростатического поля — это незамкнутые линии: они начинаются на поверхности положительных зарядов и оканчиваются на поверхности отрицательных зарядов (или в бесконечности). В-третьих, линии напряжённости не должны пересекаться, так как в каждой точке поля вектор напряжённости имеет лишь одно направление.

И, наконец, чтобы линии напряжённости отображали не только направление, но и модуль напряжённости поля, на рисунках их условились проводить с определённой густотой: их рисуют гуще там, где модуль напряжённости поля больше, и реже — где он меньше.

На рисунке вы видите пример линий напряжённости двух пластин, заряды которых равны по модулю и противоположны по знаку.

Обратите внимание, что в пространстве между пластинами линии напряжённости практически параллельны друг другу (за исключением пространства вблизи краёв пластин и вне области их перекрытия) и находятся на равных расстояниях друг от друга: здесь электростатическое поле одинаково во всех точках. Так вот, если напряжённость поля одинакова во всех его точках, то такое поле называется однородным.

Теперь давайте посмотрим, как рассчитывается напряжённость электростатического поля, созданного точечным зарядом, модуль которого равен |Q|. Для этого поместим в некоторую точку поля положительный пробный заряд q₀.

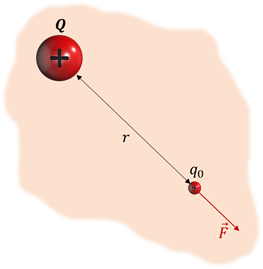
Согласно закону Кулона, на пробный заряд со стороны поля будет действовать сила, модуль которой прямо пропорционален произведению модулей обоих зарядов и обратно пропорционален квадрату расстояния между зарядом, создающим поле, и точкой, в которую помещён пробный заряд:

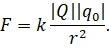
Далее вспомним, что по определению, модуль напряжённости в данной точке поля равен отношению модуля силы, с которой поле действует на пробный заряд, находящийся в выбранной точке, к величине этого заряда:

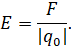
Подставим выражение для модуля кулоновской силы в формулу для модуля напряжённости поля:

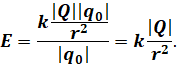
По полученной формуле мы с вами можем рассчитать напряжённость в любой точке поля, созданного неподвижным точечным зарядом.

Если же точечный заряд, создающий поле, находится в какой-либо проводящей среде, то в знаменатель формулы следует добавить множитель значения её диэлектрической проницаемости ε:

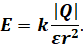
По этой же формуле можно рассчитывать напряжённость поля, образованного равномерно заряженным шаром в точках, которые находятся на его поверхности и вне его. Внутри же заряженного шара (или проводящей сферы), как мы увидим дальше, напряжённость поля равна нулю:

А теперь давайте подумаем, как найти напряжённость в некоторой точке поля, если оно создано не одним, а несколькими зарядами.

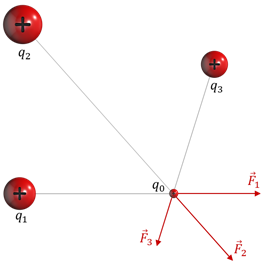
Очевидно, что если поместить в исследуемую точку такого поля пробный заряд, то на него будут действовать кулоновские силы со стороны каждого из зарядов в отдельности, создающих поле. Из механики мы знаем, что если на тело действует несколько сил, то результирующая сила равна их геометрической сумме. То же самое справедливо и для электрических сил:

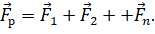
Разделим записанное равенство на величину пробного заряда:

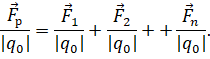
И учтём, что отношение силы, действующей на пробный заряд со стороны электрического поля, к величине этого заряда, есть напряжённость:

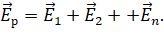
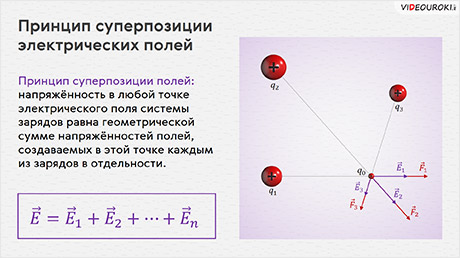
Последнее равенство выражает принцип суперпозиции полей: напряжённость в любой точке электрического поля системы зарядов равна геометрической сумме напряжённостей полей, создаваемых в этой точке каждым из зарядов в отдельности:

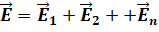
При этом напряжённость поля, создаваемого отдельным зарядом, определяется так, как будто других зарядов вокруг не существует.

А теперь для закрепления материала решим с вами несколько задач. Задача 1. Заряженный шарик радиусом 5 сантиметров находится в среде, диэлектрическая проницаемость которой равна 2. Найдите напряжённость поля в точке, удалённой от поверхности шарика на 3 сантиметра, если заряд шарика равен 3 пКл.

Задача 2. Электрическое поле создаётся двумя точечными зарядами 30 нКл и – 10 нКл, находящимися в вакууме на расстоянии 5 см друг от друга. Определите напряжённость поля в точке, находящейся на расстоянии 3 см от первого заряда и 4 см от второго.