На прошлом уроке мы с вами говорили о том, что линза — это прозрачное тело, ограниченное криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями. Она служит для управления световыми пучками, а именно для изменения направления лучей.
До сих пор мы с вами не знаем, как построить изображение предмета в тонкой линзе? Ответу на этот вопрос и будет посвящён наш урок.
Для начала рассмотрим, как получить изображения точечного источника света в собирающей и рассеивающей линзах. Для этого мы с вами будем в основном пользоваться тремя «удобными лучами» — это лучи, ход которых после прохождения через линзу нам заранее известен:
1) лучи, идущие параллельно главной оптической оси, так как после преломления в линзе, они проходят через её главный фокус (или проходят их продолжения).
2) из закона обратимости световых лучей следует, что лучи, которые идут к линзе через её фокус, после преломления будут направлены параллельно главной оптической оси — это второй набор лучей.
3) третий набор лучей выбираем исходя из того, что лучи, проходящие через оптический центр линзы, не меняют своего направления.
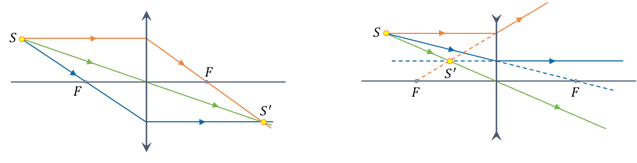
Точка пересечения преломлённых лучей в собирающей линзе или их продолжений в рассеивающей, и даёт нам положение изображения точечного источника света.
Усложним задачу. Пусть точечный источник света располагается на главной оптической оси линзы. Найдём, где образуется изображение:
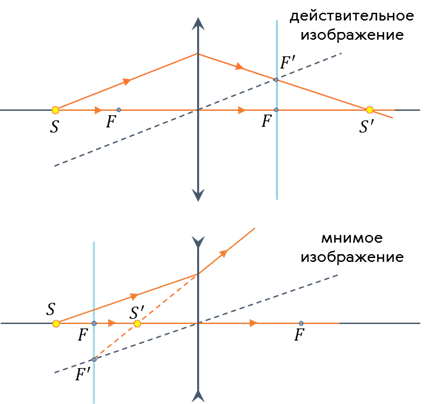
Изображение в собирающей линзе будет являться действительным, так как оно получилось на пересечении самих преломлённых лучей, а в рассеивающей — мнимым, так как оно получено на пересечении продолжений преломлённых лучей.
Теперь рассмотрим, как строятся изображения протяжённых предметов, находящихся на разных расстояниях от собирающей линзы.
Для начала рассмотрим случай, когда предмет находится за двойным фокусом линзы:

Охарактеризуем полученное изображение. Во-первых, оно действительное, так как получилось на пересечении преломлённых лучей. Во-вторых, оно перевёрнутое. И в-третьих, как можно видеть из построения, оно уменьшенное.
Обратите внимание, что если предмет расположен перпендикулярно главной оптической оси, то и его изображение также будет перпендикулярно ей. Зная это, мы сможем построить изображение точки B и опустить перпендикуляр на главную оптическую ось, что мы и будем делать в дальнейшем.
Аналогичным способом, можно построить и охарактеризовать изображение предмета, находящегося на других расстояниях от линзы.
Предмет расположен во втором фокусе линзы.
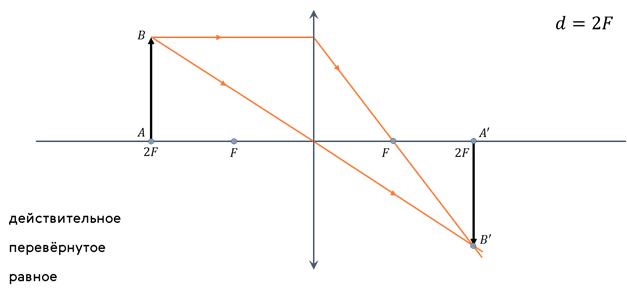
Предмет находится между первым и вторым фокусом линзы.
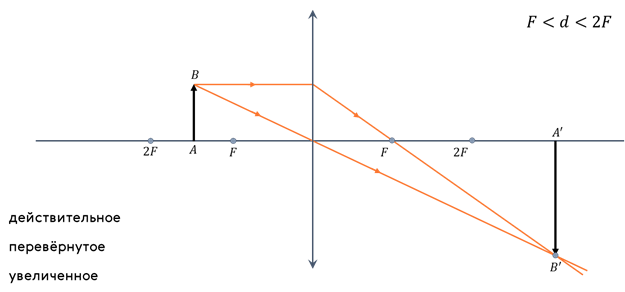
Такие изображения получаются, например, на экране кинотеатра. Оно увеличенное — экран намного больше плёнки, на которой записан фильм. На экране реально существует светящаяся картинка. А чтобы фильм не шёл вверх ногами, потому что изображение перевёрнутое, в проекторе стоит система линз, каждая из которых вносит свой вклад в изменение хода лучей.
Построим изображение предмета, находящегося в главном фокусе линзе.
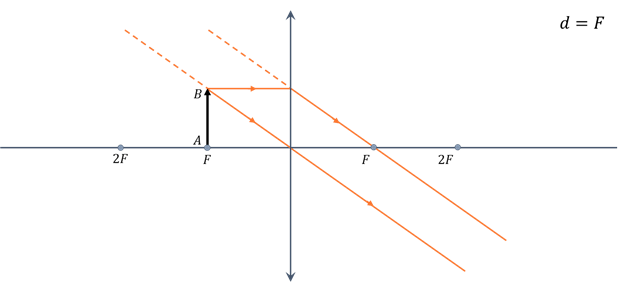
Как видим, преломлённые линзой лучи не пересекаются, как и не пересекаются их продолжения. Следовательно, изображения в этом случае нет.
И нам осталось рассмотреть последний случай, когда предмет находится между главным фокусом и линзой.
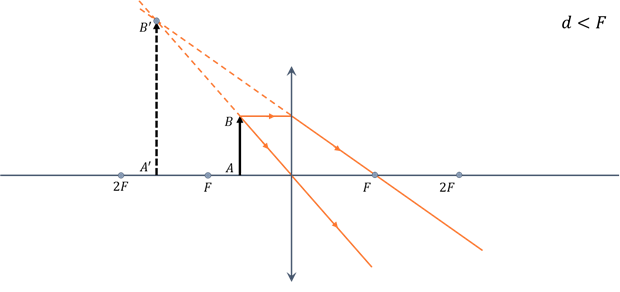
Обратите внимание, что в этом случае преломлённые лучи расходятся, а пересекаться будут только их продолжения. Поэтому изображение предмета будет мнимым, увеличенным, прямым и находиться со стороны изображаемого предмета.
Такое изображение мы получаем, например, когда пользуемся увеличительным стеклом для рассмотрения мелких объектов. Получается прямое увеличенное изображение, которое нам видно намного лучше, чем сам предмет. Но, заглянув за увеличительное стекло, увидим, что на самом деле этого увеличенного предмета там нет, то есть изображение мнимое.
При построении изображения действительного предмета в рассеивающей линзе поступают точно так же, как и в случае с собирающей. Единственное отличие состоит в том, что у рассеивающей линзы фокус мнимый.
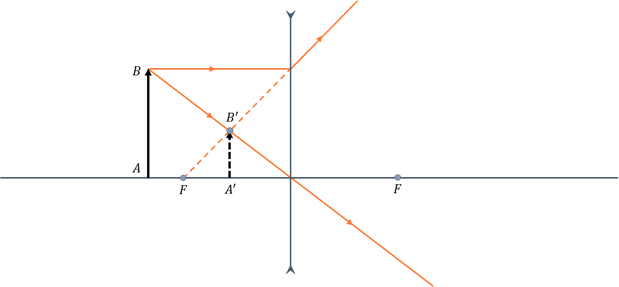
Изображение, даваемое рассеивающей линзой, всегда мнимое, прямое, уменьшенное и находится между линзой и её фокусом со стороны изображаемого предмета.
Теперь выведем формулу, которая свяжет три величины — расстояние от предмета до линзы, расстояние от линзы до изображения и фокус линзы. Для этого рассмотрим собирающую линзу, предмет АВ и его изображение в этой линзе A’B’.
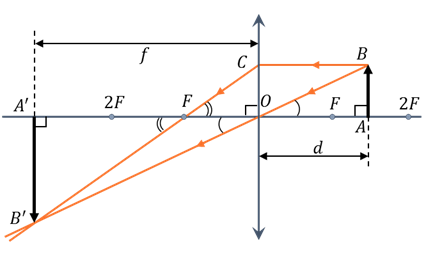

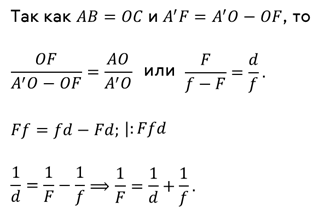
В общем виде, формула тонкой линзы записывается следующим образом: сумма величин, обратных расстояниям от предмета до линзы и от линзы до изображения, равна величине, обратной фокусному расстоянию:
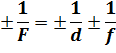
Для практического использования формулы тонкой линзы, нам следует запомнить правило знаков:
для собирающей линзы, действительных источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают положительными;
для рассеивающей линзы, мнимых источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают отрицательными.
Стоит сразу отметить, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей, продолжения которых пересекаются в одной точке.
Как вы могли заметить, чаще всего, изображение, получаемое с помощью тонкой линзы, отличается своими размерами от предмета. Так вот, это различие между размерами предмета и размерами его изображения принято характеризовать линейным (или поперечным) увеличением линзы.
Если обозначить размеры предмета h, а размеры изображения — H, то линейное увеличение линзы равно отношению линейного размера изображения к линейному размеру предмета:


 Получите свидетельство
Получите свидетельство Вход
Вход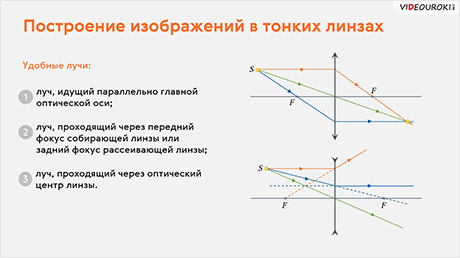




 15619
15619

