Разнообразие отношений объектов и их множеств. Отношения между множествами

Вопросы занятия:

·                   отношение;

·                   схема отношений;

·                   отношения между множествами.

Итак, на первом уроке мы узнали, что такое объект и какие отличительные признаки он имеет. Объект также можно охарактеризовать с помощью отношений, в которых этот объект находится с другими объектами.

Подробнее разберём на примерах.

Антон сын Юрия. Эйфелева башня находится в Париже. Кислород входит в состав воды.

Москва – столица России (является столицей). Антон дружит с Аней.

В данных примерах выделено имя отношения, которое обозначает характер связи между ними.

Таким образом, отношение – это взаимосвязь между объектами.

Одинаковыми отношениями могут быть связаны одновременно несколько объектов.

Например,

ученик Антон решил составить генеалогическое дерево своей семьи.

Для этого ему необходимо было узнать, кто в каких отношениях находится. То есть он приходится сыном своего отца (Юрия) и мамы (Татьяны). В свою очередь Татьяна приходится дочерью Леонида (дедушка Антона) и Елены (бабушка Антона). Юрий приходится сыном Григория (дедушка Антона) и Марии (бабушка Антона). Так же у Антона есть сестра Маша. Так как словесное восприятие вызывает затруднение, давайте поможем Антону представить это все в виде схемы и постоим генеалогическое дерево.

Видим, что самыми старшими являются дедушки и бабушки Антона, поэтому расположим их в самом верху.

У Леонида и Елены есть дочь Татьяна, а у Григория и Марии сын Юрий. Значит, разместим их на втором уровне (если считать сверху) и укажем их отношения с родителями в виде стрелок.

У Татьяны и Юрия есть сын Антон и дочь Маша. Разместим их аналогичным образом на нашей схеме.

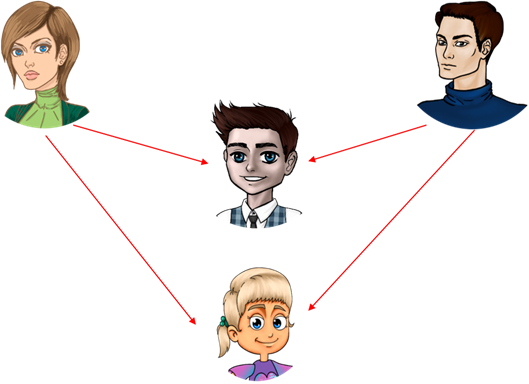
На данной схеме стрелками указаны отношения, то есть сверху вниз стрелка обозначает, что тот, кто находится выше – приходится отцом или матерью, а тот, кто ниже – приходится сыном или дочерью. В данном случае можно обойтись и без стрелок. Получим следующую схему.

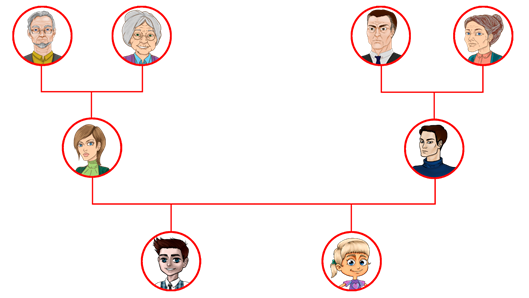
Таким образом, мы узнали, как же можно схематически показать отношение между объектами.

Следует запомнить, что такими отношениями могут быть связаны только объекты некоторых видов. А в отношениях «является элементом множества», «входит в состав» и «является разновидностью» могут находиться любые объекты.

Подходя к рассмотрению отношений множеств, разберём несколько примеров.

Для начала рассмотрим, как отношения связывают два множества.

помидоры – это овощи (являются элементом множества);

тигры относятся к семейству кошачьих;

10 входит в состав двухзначных чисел.

Для графического представления множеств удобнее использовать круги Эйлера.

Существует два каких-то множества A и B (изобразим в виде двух кругов). Итак, если множества имеют общие элементы, то есть элементы одновременно принадлежат и множеству A, и множеству B, то эти множества пересекаются.

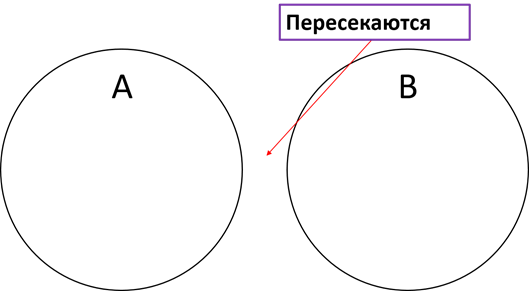
Например, Антон учится в 6 «А» классе. В классе восемнадцать человек: 8 мальчиков и 10 девочек.

У трёх девочек и у троих мальчиков по математике оценка пять. Учительница по математике попросила девочек и мальчиков, которые знают математику на пять сесть на средний ряд.

Для решения этого примера изобразим графически два множества: A – множество мальчиков, B – множество девочек. Так, как и в одном и во втором множестве есть ученики, которые знают математику на пять – объединим их и получим следующее.

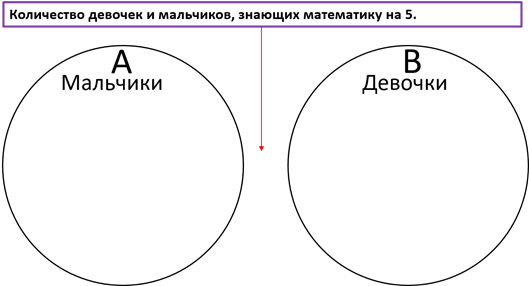
Пересечением множеств и является количество девочек и мальчиков, знающих математику на пять, то есть это те учащиеся, которые сели на средний ряд.

Множества, не имеющие общих элементов, не пересекаются.

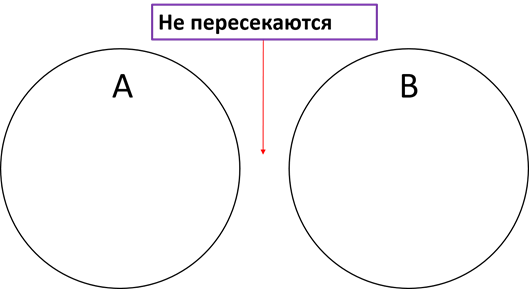
Разберём все тот же пример. В классе у Антона восемнадцать человек: восемь мальчиков и десять девочек. Возьмём A – множество мальчиков, B – множество девочек. Так как ничего общего, указанного в данном примере, между этими двумя множествами нет, то они не пересекаются.

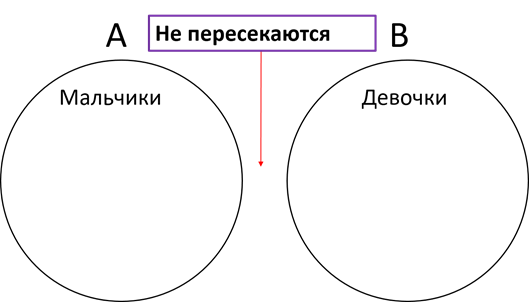
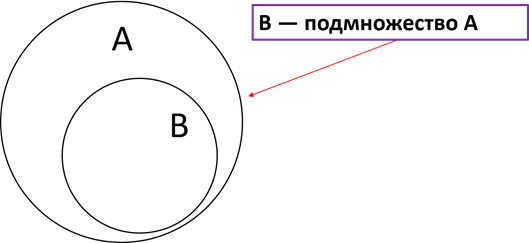
Если каждый элемент множества B является элементом множества A, то B является подмножеством A.

И снова возвращаемся к примеру, с классом Антона. Антон учится в 6 «А» классе. В классе восемнадцать человек. В школе учатся четыре шестых класса. Пусть A – множество параллели шестых классов, B – множество 6 «А» класса. Таким образом, каждый учащийся 6 «А» класса также является учащимся параллели шестых классов. То есть множество B является подмножеством A.

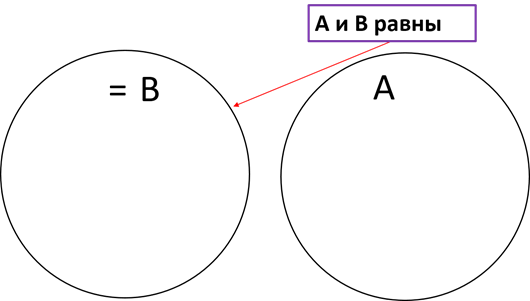
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то множества А и В равны.

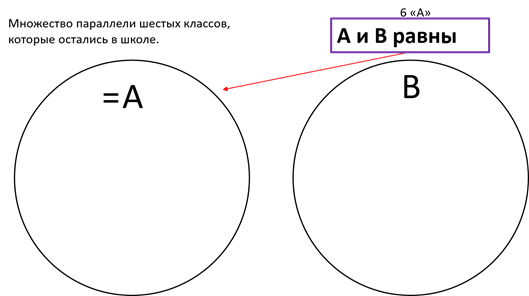
Например, Антон учится в 6 «А» классе. В школе учатся четыре шестых класса – 6 «А», 6 «Б», 6 «В», 6 «Г». Три из четырёх классов – 6 «Б», 6 «В» и 6 «Г» отправились на экскурсию и в школе из всей параллели 6-х классов остался один 6 «А». Итак, пусть A – множество параллели шестых классов, которые остались в школе, B – множество 6 «А» класса. Таким образом, каждый учащийся 6 «А» класса также является учащимся параллели шестых классов, которые остались в школе. То есть множество B равно множеству A.

Необходимо запомнить.

Отношение – это взаимосвязь между объектами.

Если два множества имеют общие элементы, т.е. элементы одновременно принадлежат и первому и второму множеству, то эти множества пересекаются.

Множества, не имеющие общих элементов, не пересекаются.

Если каждый элемент множества B является элементом множества A, то B является подмножеством A.

Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то множества А и В равны.