Вопросы занятия:
· повторить понятие «десятичные дроби», правила их записи;
· повторить способы представления обыкновенной дроби в виде десятичной;
· вспомнить правила сравнения десятичных дробей;
· правила округления десятичных дробей;
· повторить порядок выполнения действий над десятичными дробями.
Материал урока
Дробь, у которой знаменатель равен разрядной единице, то есть десяти, ста, тысяче и так далее можно записать особым способом, в виде десятичной дроби. При этом сначала пишут целую часть, а затем после запятой записывают числитель. Особое внимание нужно обращать на то, что количество знаков после запятой соответствует числу нулей разрядной единицы, стоящей в знаменателе.

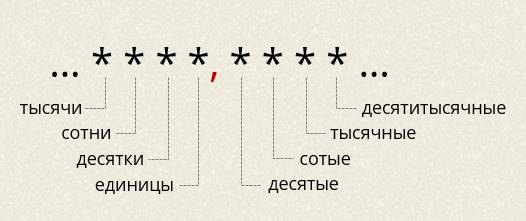
Видим, что в записи любой десятичной дроби присутствует и целая, и дробная части. Напомним разряды целой и дробной частей десятичной дроби. У целой части выделяют разряд единиц, разряд десятков, разряд сотен, разряд тысяч и так далее. Теперь назовём разряды дробной части: разряд десятых, разряд сотых, разряд тысячных, разряд десятитысячных и так далее.
Вы помните, что в конце дробной части десятичной дроби можно дописывать и отбрасывать нули, при этом значение дроби не изменится. Это удобно использовать при выполнении действий над десятичными дробями и при сравнении десятичных дробей.
Прежде чем приступить к повторению этих вопросов, напомним правила записи десятичных дробей.
Пример.

Как обыкновенные дроби с разрядной единицей в знаменателе мы записали в виде десятичных, так и, наоборот, десятичные можно записывать в виде обыкновенных.
Пример.

Теперь поговорим о сравнении. Десятичные дроби сравнивают поразрядно, начиная со старшего разряда (слева направо).
Пример.

Далее давайте вспомним правила сложения и вычитания десятичных дробей. Эти действия выполняют по тем же правилам, что и для целых чисел, только при записи столбцов вычисления запятую записывают под запятой и у результата её ставят в том же месте.

А теперь напомним правило умножения десятичных дробей. При этом вычисления производят как с обычными числами, не взирая на запятую, а затем у результата запятую ставят так, чтобы число знаков после запятой равнялось сумме знаков после запятой у множителей.
Причём, если в произведении меньше цифр, чем нужно отделить запятой, то слева нужно дописать необходимое число нулей.
Обратите внимание, вычисления выполнены также, как и над целыми числами.

Ещё стоит вспомнить два случая умножения десятичных дробей на разрядную единицу.
При умножении десятичной дроби на 10, 100, 1000 и так далее, запятую у дроби переносят вправо на количество нулей в разрядной единице.

А при умножении десятичной дроби на одну десятую, одну сотую, одну тысячную и так далее, запятую у дроби переносят влево на количество цифр после запятой в разрядной единице.

Рассмотрим конкретный пример деления десятичной дроби на число.

При делении десятичной дроби на другую десятичную дробь нужно перенести запятые в делимом и делителе на число десятичных знаков в делителе, то есть сделать делитель целым числом.

При делении десятичной дроби на 10, 100, 1000 и так далее, запятую у дроби переносят влево на количество нулей в разрядной единице.

А при делении десятичной дроби на одну десятую, одну сотую, одну тысячную и так далее, запятую у дроби переносят вправо на количество цифр после запятой в разрядной единице.

Часто можно встретить задания, в которых нужно работать с обыкновенными и десятичными дробями одновременно. Поэтому стоит напомнить способы представления обыкновенной дроби в виде десятичной.

Так мы с вами показали, что обыкновенную дробь можно представить, как в виде конечной десятичной дроби, так и в виде бесконечной периодической десятичной дроби.
Как видите не всегда обыкновенную дробь можно представить в виде конечной десятичной. Поэтому стоит напомнить, что обыкновенную несократимую дробь можно перевести в конечную десятичную, если разложение знаменателя на простые множители содержит только цифры 2 и 5.
Далее вспомним правило округления десятичной дроби.
Определение.
Округлить число — это значит заменить его «круглым числом» с нулями на конце или с укороченной дробной частью в зависимости от того, до какого разряда производится округление.
Подчеркнув цифру округляемого разряда, обращаем внимание на ту, которая стоит справа.
Если это 0, 1, 2, 3 или 4, то подчёркнутую цифру оставляем той же.
Если это 5, 6, 7, 8 или 9, то подчёркнутую цифру увеличиваем на единицу.
Цифры справа от округляемого разряда, стоящие после запятой отбрасываем. А те, которые стоят до запятой, заменяем нулями.

Далее выполним задание, где нужно найти значения выражений, содержащих как обыкновенные, так и десятичные дроби.
Пример

Итоги урока
В подведении итогов урока напомним все его основные моменты.
Мы вспомнили, что за дроби называют десятичными, и повторили правила их записи. Напомнили способы представления обыкновенной дроби в виде десятичной.
А также повторили правила сравнения десятичных дробей, правила их округления и правила выполнения арифметических действий над десятичными дробями.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 5803
5803