Вопросы занятия:
· познакомиться с понятием непрерывной функции;
· познакомиться с понятием предел функции в точке;
· рассмотреть примеры использования данных понятий для решения задач.
Материал урока.
Прежде чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.

Не всегда нам надо знать точные значения тех или иных параметров. Иногда нам достаточно знать, как они изменяются. Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на сколько именно изменилась температура воздуха, а нам важно похолодало или потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а важно определить разгоняется автомобиль или тормозит.
Причём, если на улице потеплело, то изменения будут со знаком плюс и наоборот если похолодало, то изменения будут со знаком минус.
Если автомобиль разгоняется, то изменения будут со знаком плюс, если тормозит – то со знаком минус.
Для описания таких изменений было введено понятие приращение.
Определение.
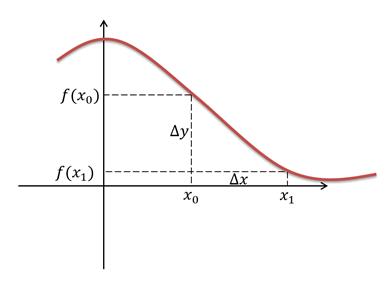
Пусть функция y = f(x) определена в точках x0 и x1. Разность x1 – x0 называют приращением аргумента, а разность f(x1) – f(x0) называют приращением функции.
Приращение аргумента обозначают так:

Приращение функции обозначают так:

Давайте рассмотрим, что же такое приращение аргумента и функции на графике.
Рассмотрим пример.
Пример.

Рассмотрим ещё один пример.
Пример.

Давайте вспомним определение непрерывной функции, которое мы формулировали ранее.
Определение непрерывности функции в точке x = a выглядит так:
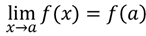
Определение непрерывности функции в точке можно записать так:

Когда мы вводили определение непрерывной функции, то мы говорили, что функция непрерывна на промежутке X, если она непрерывна в каждой точке промежутка. Давайте уточним, что означает непрерывность функции в концевых точках промежутка, например, как понимать непрерывность функции в точках a и b отрезка [a; b].
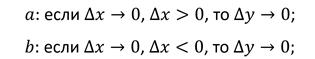
Рассмотрим пример.
Пример.

Давайте изобразим график линейной функции. Отметим приращение аргумента и функции. И найдём чему равно отношение приращения аргумента к приращению функции.

Рассмотрим пример.
Пример.


 Получите свидетельство
Получите свидетельство Вход
Вход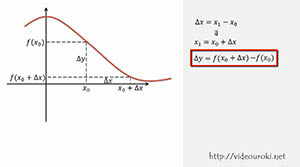



 0
0 10087
10087