Напомним,
что уравнение, которое содержит переменную под знаком тригонометрических
функций, называется тригонометрическим уравнением. Уравнения вида
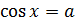 ,
, 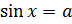 ,
, 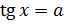 и
и 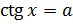 , где х – переменная,
а число
, где х – переменная,
а число 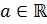 , называются простейшими
тригонометрическими уравнениями. На этом уроке мы с вами подробно
рассмотрим решение уравнений вида
, называются простейшими
тригонометрическими уравнениями. На этом уроке мы с вами подробно
рассмотрим решение уравнений вида 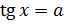 и
и 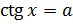 .
.
Вы
уже знаете, что тангенсом угла 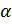 называется отношение
синуса угла
называется отношение
синуса угла 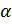 к его косинусу. А котангенсом
угла
к его косинусу. А котангенсом
угла 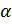 называется отношение
косинуса угла
называется отношение
косинуса угла 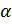 к синусу угла
к синусу угла 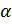 .
.
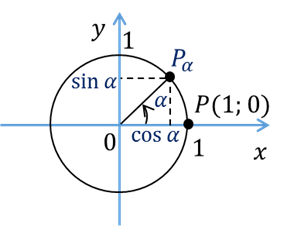
Важно
помнить, что 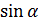 и
и 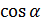 определены для любого
угла
определены для любого
угла 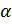 , а их значения заключены
в промежутках от минус единицы до единицы, так как координаты точек единичной
окружности заключены в промежутках –1 до 1.
, а их значения заключены
в промежутках от минус единицы до единицы, так как координаты точек единичной
окружности заключены в промежутках –1 до 1.
А
вот тангенс 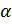 определён только для тех
углов, для которых косинус
определён только для тех
углов, для которых косинус 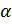 не
равен нулю, так как делить на нуль нельзя. Тогда тангенс
не
равен нулю, так как делить на нуль нельзя. Тогда тангенс 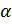 определён
для любых углов, кроме
определён
для любых углов, кроме 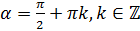 .
.
Что
касается котангенса 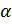 , то он определён только
для тех углов, для которых синус
, то он определён только
для тех углов, для которых синус 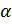 не
равен нулю. То есть котангенс
не
равен нулю. То есть котангенс 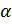 определён
для любых углов, кроме
определён
для любых углов, кроме 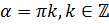 .
.
Исходя
из определений тангенса и котангенса, следует, что 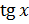 и
и 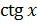 могут принимать любые действительные
значения. Значит, уравнения
могут принимать любые действительные
значения. Значит, уравнения 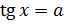 и
и 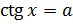 имеют корни при любом
значении а.
имеют корни при любом
значении а.
Так
как же решают такие уравнения? Давайте рассмотрим два уравнения: 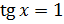 и
и 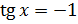 .
.
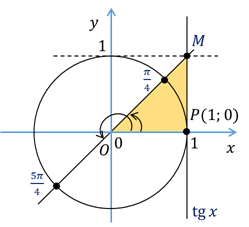
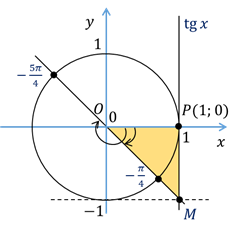
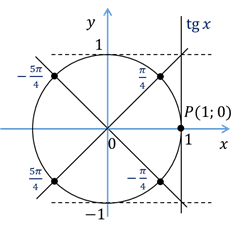
Решение этих уравнений удобно проиллюстрировать с помощью линии тангенсов. Напомним, что тангенс икс – это ордината точки М пересечения прямой ОМ с линией тангенсов.
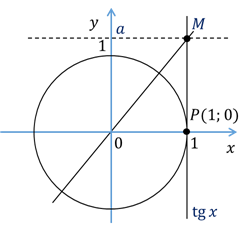
Итак,
построим углы, тангенсы которых равны 1. Для этого через начальную точку Р
проведём прямую, перпендикулярную оси абсцисс, то есть линию тангенсов. На
линии тангенсов есть лишь одна точка с ординатой один. Обозначим её М. Затем
через точку М и начало координат проведём прямую. Обратите внимание, эта прямая
пересекает единичную окружность в двух диаметрально противоположных точках –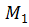 и
и 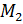 . Видим, у нас получился
прямоугольный треугольник РОМ. Вы уже знаете, что тангенсом угла в прямоугольном
треугольнике называется отношение противолежащего катета к прилежащему
. Видим, у нас получился
прямоугольный треугольник РОМ. Вы уже знаете, что тангенсом угла в прямоугольном
треугольнике называется отношение противолежащего катета к прилежащему 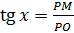 . Найдём это отношение.
Так как РО равно 1, то имеем
. Найдём это отношение.
Так как РО равно 1, то имеем  .
.
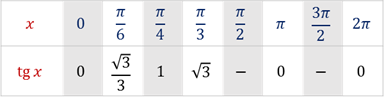
Отсюда
по таблице значений 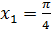 . Таким образом, точка
. Таким образом, точка 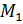 получается путём
поворота начальной точки на угол
получается путём
поворота начальной точки на угол  . В свою очередь, точка
. В свою очередь, точка 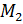 получается поворотом
начальной точки на угол
получается поворотом
начальной точки на угол 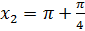 .
.
Но
ведь в эти точки мы можем попасть не по одному разу. Если мы сделаем полный
оборот по единичной окружности, то снова попадём в эти точки. Сделав ещё полный
оборот, снова попадём в эти точки и так далее. Отсюда 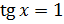 имеет две серии решений:
имеет две серии решений:
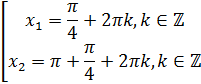
Как
правило, эти серии решений совмещают и записывают как 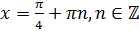 .
.
Решим
второе уравнение 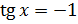 . Оно решается
аналогичным образом. Итак, построим углы, тангенсы которых равны –1. Для этого
проведём линию тангенсов. На линии тангенсов есть лишь одна точка с ординатой –1.
Обозначим её М. Затем через точку М и начало координат проведём прямую. Эта
прямая пересекает единичную окружность в двух диаметрально противоположных
точках –
. Оно решается
аналогичным образом. Итак, построим углы, тангенсы которых равны –1. Для этого
проведём линию тангенсов. На линии тангенсов есть лишь одна точка с ординатой –1.
Обозначим её М. Затем через точку М и начало координат проведём прямую. Эта
прямая пересекает единичную окружность в двух диаметрально противоположных
точках – 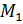 и
и 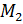 . Видим, у нас получился
прямоугольный треугольник РОМ. Так как тангенс угла в прямоугольном
треугольнике – это отношение противолежащего катета к прилежащему
. Видим, у нас получился
прямоугольный треугольник РОМ. Так как тангенс угла в прямоугольном
треугольнике – это отношение противолежащего катета к прилежащему 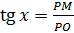 , то
, то 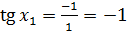 . Отсюда
. Отсюда 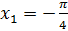 . Таким образом, точка
. Таким образом, точка 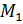 получается путём
поворота начальной точки на угол
получается путём
поворота начальной точки на угол 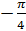 . В свою очередь, точка
. В свою очередь, точка 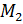 получается поворотом
начальной точки на угол
получается поворотом
начальной точки на угол 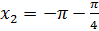 .
.
Отсюда
уравнение 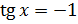 имеет две серии решений:
имеет две серии решений:
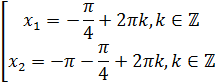
Как
правило, эти серии решений совмещают и записывают как 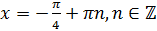 .
.
Заметим,
что каждое из уравнений 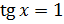 и
и 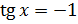 имеет бесконечное
множество корней. Однако на интервале
имеет бесконечное
множество корней. Однако на интервале 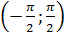 каждое из этих уравнений
имеет только один корень. Так,
каждое из этих уравнений
имеет только один корень. Так, 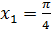 , – это корень уравнения
, – это корень уравнения 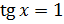 , а
, а 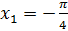 , – это корень уравнения
, – это корень уравнения 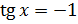 . Число
. Число  называют арктангенсом
числа 1. Записывают так:
называют арктангенсом
числа 1. Записывают так: 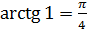 . Число
. Число 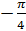 называют арктангенсом
числа –1. Записывают так:
называют арктангенсом
числа –1. Записывают так: 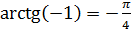 .
.
Кстати, «арктангенс» в переводе с латинского означает «дуга» и «тангенс». Это обратная функция.
Вообще,
уравнение 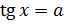 для любого
для любого 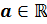 на интервале
на интервале 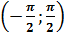 имеет только один
корень. Если
имеет только один
корень. Если 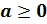 , то этот корень заключён
в промежутке
, то этот корень заключён
в промежутке 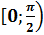 ;
;
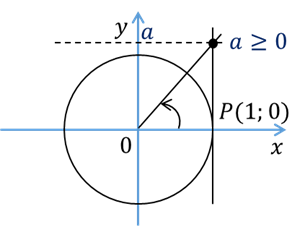
если
же 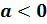 , то корень располагается
в промежутке
, то корень располагается
в промежутке 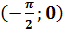 .
.
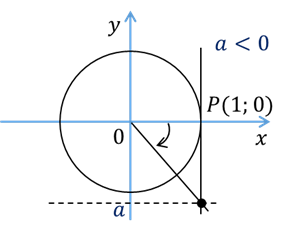
Этот
корень называют арктангенсом числа а и обозначают так 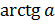 .
.
Запомните! Арктангенсом
числа 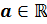 называется
такое число
называется
такое число 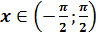 , тангенс которого равен
а.
, тангенс которого равен
а.
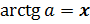 , если
, если 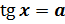 и
и 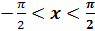
Например,
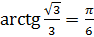 , так как
, так как 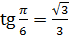 ,
, 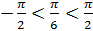 .
. 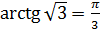 , так как
, так как 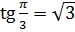 ,
, 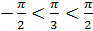 .
.
Возвращаясь
к нашему уравнению 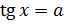 , где
, где 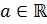 , можно утверждать, что
все корни уравнения можно найти по формуле:
, можно утверждать, что
все корни уравнения можно найти по формуле: 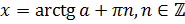 . Это и есть общая
формула нахождения корней уравнения
. Это и есть общая
формула нахождения корней уравнения 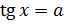 .
.
Запомните!
Для любого 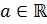 справедлива формула
справедлива формула 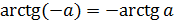 . Эта формула позволяет
находить значения арктангенсов отрицательных чисел через значения арктангенсов
положительных чисел.
. Эта формула позволяет
находить значения арктангенсов отрицательных чисел через значения арктангенсов
положительных чисел.
Например,
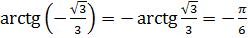 .
.
Уравнения
вида 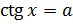 решаются аналогичным
образом. Отличия лишь в том, что
решаются аналогичным
образом. Отличия лишь в том, что 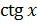 – это абсцисса точки М
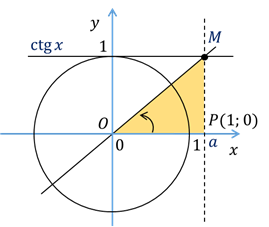
пересечения прямой ОМ с линией котангенсов. И при построении углов, котангенсы
которых нужно найти, из прямоугольного треугольника мы будем находить отношение
прилежащего катета к противолежащему, так как котангенсом
угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему
– это абсцисса точки М
пересечения прямой ОМ с линией котангенсов. И при построении углов, котангенсы
которых нужно найти, из прямоугольного треугольника мы будем находить отношение
прилежащего катета к противолежащему, так как котангенсом
угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему
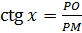 . Вычислив
это отношение, мы найдём искомое решение уравнения.
. Вычислив
это отношение, мы найдём искомое решение уравнения.
Уравнение 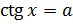 также имеет
бесконечное множество решений при любых значениях а. Однако
на интервале
также имеет
бесконечное множество решений при любых значениях а. Однако
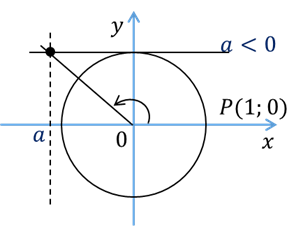
на интервале 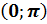 это уравнение для любого
действительного а имеет только один корень. Если
это уравнение для любого
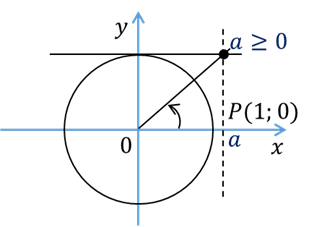
действительного а имеет только один корень. Если 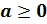 , то этот корень заключён
в промежутке
, то этот корень заключён
в промежутке 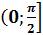 ;
;
если
же 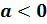 , то корень располагается
в промежутке
, то корень располагается
в промежутке 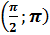 .
.
Этот
корень называют арккотангенсом числа а и обозначают так 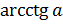 .
.
Запомните! Арккотангенсом
числа 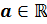 называется
такое число
называется
такое число 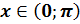 , котангенс которого
равен а.
, котангенс которого
равен а.
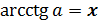 , если
, если 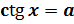 и
и 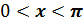
Например,
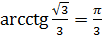 , так как
, так как 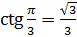 ,
, 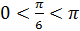 .
. 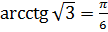 , так как
, так как 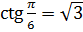 ,
, 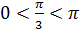 .
.
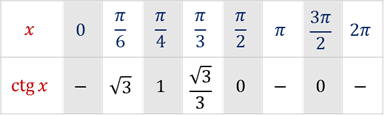
Тогда можно утверждать, что все корни уравнения 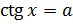 можно найти
по формуле:
можно найти
по формуле: 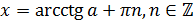 . Это и есть
общая формула нахождения корней уравнения котангенс икс равно а.
. Это и есть
общая формула нахождения корней уравнения котангенс икс равно а.
Запомните!
Для любого 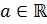 справедлива формула
справедлива формула 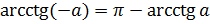 . Эта формула позволяет
находить значения арккотангенсов отрицательных чисел через значения
арккотангенсов положительных чисел.
. Эта формула позволяет
находить значения арккотангенсов отрицательных чисел через значения
арккотангенсов положительных чисел.
Например,
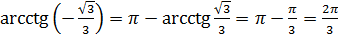 .
.
А теперь давайте приступим к практической части нашего урока.
Задание. Решите
уравнения 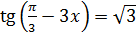 и
и 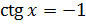 .
.
Решение.
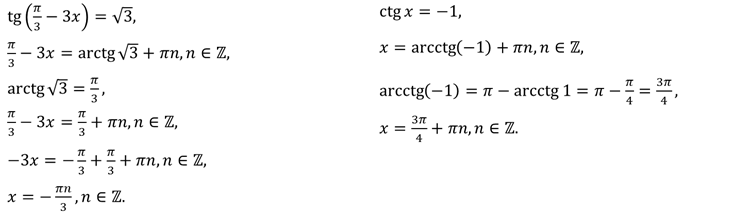

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 13183
13183

