Потенциальная энергия (практика)

Данная тема посвящена решению задач, связанных с расчетом потенциальной энергии тела.

Задача 1. В кубическом аквариуме плавает в воде массивная тонкостенная прямоугольная коробка. В дне коробки аккуратно проделали маленькое отверстие, после чего она набрала воды и утонула. Как изменилась потенциальная энергия механической системы, включающей в себя воду и коробку?

РЕШЕНИЕ

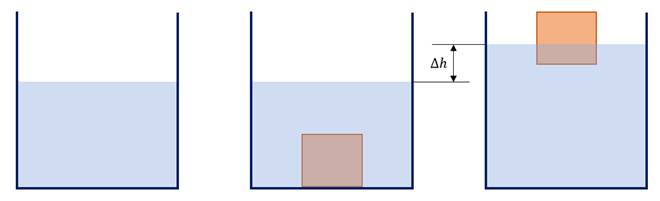
Потенциальная энергия тела в гравитационном поле Земли определяется произведением массы тела, ускорения свободного падения и высоты, на которой находится тело относительно нулевого уровня, в качестве которого выберем дно аквариума.

Так как по условию задачи коробка тонкостенная, то объем самих стенок пренебрежимо мал. Следовательно, уровень воды в аквариуме с утонувшей коробкой будет совпадать с уровнем воды, когда коробки в аквариуме вообще нет.

И так, когда коробка плавала, сила тяжести уравновешивалась архимедовой силой. А как известно, сила Архимеда равна весу вытесненной жидкости. Таким образом, уровень воды в аквариуме с плавающей коробкой выше, чем в аквариуме без коробки. Поэтому, когда коробка тонет, уровень воды уменьшается. Следовательно, уменьшается и потенциальная энергия воды, так как ее центр масс опускается. Сама коробка также опускается на дно, следовательно, ее потенциальная энергия тоже уменьшается.

ОТВЕТ: для системы «коробка-вода» потенциальная энергия уменьшится.

Задача 2. Определите массу однородного куба, находящегося на горизонтальной плоскости, если для его переворота с одной грани на соседнюю требуется совершить минимальную работу в 200 Дж. Длина ребра куба 1 м.

Задача 3. На рисунке изображена зависимость силы упругости от абсолютного удлинения пружины. Чему равно отношение работы, совершенной для увеличения абсолютного удлинения от 0 до 4 см, к работе, совершенной для абсолютного удлинения от 4 см до 8 см?

РЕШЕНИЕ

Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с обратным знаком.

Потенциальная энергия пружины определяется по формуле:

Так как в первоначальный момент времени пружина не деформирована, то ее потенциальная энергия равна нулю.

Энергия пружины в состоянии А будет равна

где х₁ — это величина абсолютного удлинения пружины при ее первом растяжении.

Аналогично будет определяться потенциальная энергия пружины в состоянии B

На основании записанных формул, составим уравнения для работы сил упругости для двух состояний

Так как нам требуется определить отношение работ, то выполним почленное деление первого уравнения на второе

ОТВЕТ: А₁/А₂ = 1/3.

Эту же задачу можно было решить и другим способом — графическим.

Известно, что работа силы численно равна площади фигуры под графиком силы. В случае, когда пружину растягивают первый раз, данной фигурой будет являться прямоугольный треугольник, площадь которого равна половине произведения его катетов.

Задача 4. Санки съезжают с горы высотой 10 м и углом наклона 30^о и движутся дальше по горизонтальному участку. Коэффициент трения на всем пути одинаков и равен 0,3. Определите расстояние, которое пройдут санки по горизонтальному участку до полной остановки.

«Очень важно не перестать задавать вопросы.

Любопытство не случайно дано человеку».

Альберт Эйнштейн