На этом уроке мы с вами вспомним основные логические операции, правила построения таблиц истинности, порядок выполнения действий в логическом высказывании и многое другое.
К основным логическим операциям относятся конъюнкция, дизъюнкция, инверсия и исключающее или.
Начнём с конъюнкции. Конъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться ложным тогда, когда хотя бы одно из исходных высказываний ложно. Конъюнкция – это двухместная операция, то есть в ней должны присутствовать две логические переменные.
В естественном языке конъюнкция соответствует союзу «И». В алгебре конъюнкция может обозначаться с помощью нескольких знаков: «&», «/\», «·». В языках программирования для обозначения конъюнкции используется союз «AND», «&» или «&&».
Таблица истинности для конъюнкции выглядит следующим образом:

Латинская буква Т – обозначает истину, а F – ложь.
В первых двух столбцах представлены все возможные исходные данные А и B.
В четвёртой строке будет истина, так как высказывания А и B оба истинны, а вот во всех остальных строках будет ложь.
Для более лёгкого запоминания таблицы истинности для конъюнкции можно представить её в виде электрической цепи с двумя последовательными выключателями.

Лампочка загорится только в том случае, если два выключателя будут включены (замкнуты), то есть когда новое высказывание будет истинно.

Во всех остальных случаях новое высказывание будет ложно.
Переходим к дизъюнкции. Дизъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет истинным тогда, когда хотя бы одно исходное высказывание истинно. Дизъюнкция также является двухместной операцией, то есть в ней должны присутствовать две логические переменные.
В естественном языке – это союз «ИЛИ». В алгебре высказываний используется следующий знак: «V» или «+». В программировании в основном используется «OR». Но в некоторых языках программирования дизъюнкция обозначается следующими знаками: «|», «||».
Таблица истинности для дизъюнкции выглядит следующим образом:

Как и в таблице истинности для конъюнкции, в первых двух столбцах предоставлены все возможные исходные данные А и B.
В первой строке у нас будет «ложь», так как значения высказываний А и B ложны, а во всех остальных строках будет «истина».
И снова для запоминания таблицы истинности можно использовать электрическую цепь с двумя параллельными выключателями.

То есть лампочка загорится в том случае, если будет включён (замкнут) хотя бы один выключатель.



Далее у нас идёт инверсия – логическое отрицание. Отрицание – это логическая операция, которая преобразует исходное высказывание в новое, значение которого противоположно исходному. А вот отрицание является унарной (одноместной) операцией.
В естественном языке инверсии соответствуют речевой оборот «НЕВЕРНО, ЧТО» и частица «НЕ». В алгебре высказывания инверсия обозначается следующими знаками: «¬», «ˉ». А вот в сфере программирования используется слово «NOT».
И снова рассмотрим таблицу истинности.

Так как инверсия – это одноместная операция, то в первом столбце предоставлены всевозможные исходные значения переменной А. Если исходное значение А было истинным, то при инверсии оно станет ложным. И наоборот, если исходное значение А было ложным, то после применения инверсии оно станет истинным.
И последняя операция, которую мы с вами рассмотрим, – исключающее ИЛИ. Исключающее ИЛИ – это логическая операция, которая объединяет два высказывания в одно новое, которое будет истинным тогда и только тогда, когда одно из исходных высказываний истинное, а второе – ложное. Исключающее ИЛИ является двухместной операцией, то есть в ней должны присутствовать две логические переменные.
Исключающее ИЛИ обозначается в программировании следующим образом: «XOR».
И снова обратимся к таблице истинности.

В первых двух столбцах предоставлены всевозможные значения А и B. Исходя из определения, мы можем сделать вывод, что во второй и третьей строках значение нового высказывания будет равно истине, так как во второй строке высказывание А – истинно, B – ложно. В третьей строке наоборот, А – ложно, B – истинно. В первой и четвёртой строках будет значение «ложь».
Если все четыре таблицы истинности объединить в одну, то мы получим следующее:

При помощи этой таблицы можно очень легко определять истинность или ложность тех или иных высказываний.
Любое логическое высказывание может состоять из логических констант и переменных, отношений, логических операций. Также оно будет принимать одно из двух значение: «истина» или «ложь».
При решении логического высказывания нужно учитывать приоритеты арифметических, логических операций и операций отношений:
1. Арифметические операции:
1) – (минус унарный);
2) *, /;
3) +, –.
2. Логические операции:
1) not;
2) and;
3) or, xor.
3. Операции отношения: =, <>, >, <, >=, <=.
Также не стоит забывать, что наибольший приоритет имеют операции в скобках.
А сейчас разберёмся на примере.
Определить, истинны или ложны следующие логические высказывания.
A = {(2 + 2 = 5 и 2 х 3 = 6) и (3 + 2 = 5 или 3 + 3 = 5) или (4 х 2 = 8 и 3 х 2 = 6)};
В = {(6 – 1= 5 или 5 – 2 = 4) и (8 + 2 = 10 и 5 х 2 = 10) и (7 + 2 = 9 или 1 + 8 = 9)}.
Начнём с высказывания А. Сначала выясним, истинны или ложны выражения в скобках. Начнём с первых скобок слева направо. Итак,
(2 + 2 = 5) = F;
(2 х 3 = 6) = T.
Но так как у нас в скобках стоит операция конъюнкции, то ложное и истинное высказывания будут давать «ложь».
(2 + 2 = 5 и 2 х 3 = 6) = F.
Переходим ко вторым скобкам.
(3 + 2 = 5) = T;
(3 + 3 = 5) = F.
Операция – дизъюнкция, значит значение всей скобки будет истинно.
(3 + 2 = 5 или 3 + 3 = 5) = T.
Последние скобки.
(4 х 2 = 8) = T;
(3 х 2 = 6) = T.
При конъюнкции двух «истин» мы получим «истину».
(4 х 2 = 8 и 3 х 2 = 6) = T.
Осталось найти значение всего высказывания. Сначала будем выполнять конъюнкцию двух первых скобок.
(2 + 2 = 5 и 2 х 3 = 6) и (3 + 2 = 5 или 3 + 3 = 5).
При конъюнкции «лжи» и «истинности» мы получим «ложь».
(2 + 2 = 5 и 2 х 3 = 6) и (3 + 2 = 5 или 3 + 3 = 5) = F и T = F.
Нам осталось найти дизъюнкцию «лжи» и «истины».
(2 + 2 = 5 и 2 х 3 = 6) и (3 + 2 = 5 или 3 + 3 = 5) или (4 х 2 = 8 и 3 х 2 = 6) = F или T.
В результате мы получим «истину», так как, исходя из определения, при дизъюнкции мы получим «истину» в том случае, если хотя бы одно высказывание истинно.
(2 + 2 = 5 и 2 х 3 = 6) и (3 + 2 = 5 или 3 + 3 = 5) или (4 х 2 = 8 и 3 х 2 = 6) = F или T = T.
A = {(2 + 2 = 5 и 2 х 3 = 6) и (3 + 2 = 5 или 3 + 3 = 5) или (4 х 2 = 8 и 3 х 2 = 6)} = T.
Переходим ко второму высказыванию.
В = {(6 – 1= 5 или 5 – 2 = 4) и (8 + 2 = 10 и 5 х 2 = 10) и (7 + 2 = 9 или 1 + 8 = 9)}.
Высказывание в первых скобках:
(6 – 1= 5) = T;
(5 – 2 = 4) = F;
(6 – 1= 5 или 5 – 2 = 4) = T или F = T.
Так как при дизъюнкции истинного и ложного высказываний мы получим «истину».
Далее вторые скобки:
(8 + 2 = 10) = T;
(5 х 2 = 10) = T;
(8 + 2 = 10 и 5 х 2 = 10) = T и T = T.
При конъюнкции двух «истин» мы получим «истину».
Третьи скобки:
(7 + 2 = 9) = T;
(1 + 8 = 9) = T
(7 + 2 = 9 или 1 + 8 = 9) = T или T = T.
При дизъюнкции двух «истин» мы получаем также «истину». Нам осталось найти значение всего высказывания. Значения всех трёх скобок – «истина».
(6 – 1= 5 или 5 – 2 = 4) = T или F = T;
(8 + 2 = 10 и 5 х 2 = 10) = T и T = T;
(7 + 2 = 9 или 1 + 8 = 9) = T или T = T.
Во всём выражении у нас конъюнкция, значит значение всего высказывания будет равно «истине».
В = {(6 – 1= 5 или 5 – 2 = 4) и (8 + 2 = 10 и 5 х 2 = 10) и (7 + 2 = 9 или 1 + 8 = 9)} = T и T и T = T.
А сейчас давайте рассмотрим правила, которые следует соблюдать при построении таблицы истинности:
1. Подсчитать n – число переменных в выражении. Мы с вами знаем, что переменные обозначаются с помощью букв латинского алфавита.
2. Подсчитать общее число логических операций в выражении. То есть нам нужно сосчитать, сколько в нашем выражении инверсий, конъюнкций и дизъюнкций.
3. Установить последовательность выполнения логических операций с учётом скобок и приоритетов. Как мы с вами знаем, сначала выполняются операции в скобках, затем инверсия, конъюнкция и дизъюнкция или исключающее ИЛИ.
4. Определить число столбцов в таблице: число переменных + число операций. То есть нам нужно сложить количество переменных и логических операций. Мы получим число столбцов в таблице.
5. Заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в пункте 3. То есть мы сначала пишем в шапке таблицы все наши переменные. Затем операции в порядке их следования.
6. Определить число строк в таблице (не считая шапки таблицы): m = 2n. m – это количество строк, n – число переменных в выражении. То есть, если наше логическое выражение будет состоять, например, из 3 переменных, то количество строк m = 23 = 8. Шапка не входит в количество этих строк.
7. Выписать наборы входных переменных с учётом того, что они представляют собой ряд целых n-разрядных двоичных чисел от 0 до 2n – 1. Здесь мы должны написать все возможные входные переменные, как мы делали при построении таблиц истинности.
8. Провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью. То есть произвести логические операции с входными данными в зависимости от логической операции.
А теперь давайте разберёмся на примере. Необходимо построить таблицу истинности для следующего логического выражения: F = Ā & (B V A).
Итак, число переменных в нашем выражении n=2, общее число логических операций равно 3. В первую очередь у нас будет выполняться операция в скобках, затем инверсия и в последнюю очередь – конъюнкция:
1) B V A;
2) Ā;
3) Ā & (B V A).
Число столбцов в нашей таблице будет равно 2 + 3 = 5.

Заполним шапку. Первых два столбца – переменные А и B. В третьем столбце будет дизъюнкция B V A, в четвёртом – Ā, в пятом – Ā & (B V A).

Число строк в таблице считается по формуле m = 2n, где n – это количество переменных. Из этого следует, что m = 2n = 22 = 4.

Заполним первых два столбца исходными данными А и B.

Третий столбец – B V A. Для заполнения будем брать данные из первых двух столбцов. При дизъюнкции новое высказывание будет ложно только тогда, когда оба исходных высказывания ложны. Из этого следует, что в первой строке будет стоять значение – «ложь», а во всех остальных – «истина».

Четвёртый столбец – Ā. Данные будем брать из первого столбца. При отрицании, если исходное высказывание было истинно, то новое будет ложно, а если исходное высказывание было ложно, то новое будет истинно. Заполним четвёртый столбец.

Пятый столбец – Ā & (B V A). Данные будем брать из третьего и четвёртого столбцов. При конъюнкции новое высказывание будет являться ложным тогда, когда хотя бы одно исходное высказывание ложно. Из этого следует, что ложные высказывания будут в первой, третьей и четвёртой строках. Во второй будет значение – «истина».

А сейчас перейдём к логическим элементам. К ним относятся конъюнктор, дизъюнктор и инвертор.
Итак, первый логический элемент И (конъюнктор). С его помощью реализуется операция логического умножения. Рассмотрим его.

А – это входные данные первого элемента, B – второго, F – выходные данные.

Исходя из таблицы истинности конъюнкции, можно сказать, что единица на выходе получится тогда и только тогда, когда на всех входах будут единицы. Или же, другими словами, в результате мы можем получить для F единицу тогда и только тогда, когда А и B равны единице.
Следующий логический элемент – ИЛИ (дизъюнктор).

Как вы уже, наверное, догадались, с его помощью реализуется операция логического сложения.

И снова исходя из таблицы истинности для дизъюнкции, можно сказать, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. То есть, если А или B будут равны единице, то F также будет равно единице.
И последний логический элемент – НЕ (инвертор).

С его помощью реализуется операция отрицания. Здесь всё просто. Снова нам понадобится таблица истинности для инверсии.

Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. То есть, если А = 0, то F = 1. И, если А = 1, то F = 0.
Давайте построим логическую схему для логической функции, которую мы с вами рассматривали ранее.
F = Ā & (B V A).
У нас две переменных: А и B. Обозначим их.

Первая операция, которую мы должны выполнить, – B V A. Изобразим дизъюнктор и проведём к нему линии от А и B.

Также отдельно необходимо изобразить инвертор и провести к нему линии от А.

И последний логический элемент – конъюнктор. Изобразим его и проведём к нему прямые от инвертора и дизъюнктора.

На выходе из конъюнктора мы получим значение функции.
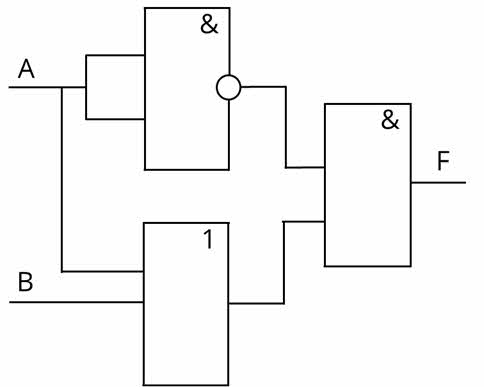
Мы с вами построили логическую схему для нашей функции. Таблицу истинности для неё мы с вами уже строили ранее.

Нам осталось вспомнить основные свойства логических операций.
Их называют законами алгебры логики.
1. Переместительный (коммутативный) закон. При перестановке местами переменных в конъюнкции и дизъюнкции значение выражения не изменяется.

2. Сочетательный (ассоциативный) закон. Если в выражении все операции одинаковы, например, две конъюнкции, то скобки можно ставить произвольно или вообще опускать.

3. Распределительный (дистрибутивный) закон.

4. Закон двойного отрицания. Двойное отрицание исключает отрицание.

5. Закон исключённого третьего. Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе – ложно, третьего не дано.

6. Закон повторения. Этот закон говорит о том, что при конъюнкции или дизъюнкции одного и того же высказывания, получится это же высказывание.

7. Законы операций с нулём и единицей.

8. Закон общей инверсии. Для того, чтобы найти инверсию конъюнкции, нужно найти дизъюнкцию инверсий каждого логического выражения. Для того, чтобы найти инверсию дизъюнкции, нужно найти конъюнкцию инверсий каждого логического выражения.

Все законы алгебры логики можно доказать с помощью таблиц истинности.
Рассмотрим ещё один пример.
Упростить логическое выражение (Ā V B) & (A V B).
Смотрим внимательно на наше выражение. Можем заметить, что в нём в обеих скобках встречается переменная B. Давайте воспользуемся первым законом:

И поставим переменную B на первое место в каждой из скобок, так как от перемены мест в данном случае ничего не изменится:
(Ā V B) & (A V B) = (B V Ā) & (B V A).
А сейчас посмотрим на третий закон – распределительный.

Исходя из него, мы можем преобразовать наше выражение, и получим:
(Ā V B) & (A V B) = (B V Ā) & (B V A) = B V (Ā & A).
Исходя из пятого закона, исключённого третьего, при Ā & A мы получим 0.

Значит, при упрощении нашего выражения в результате мы получим то, что оно равно B.
(Ā V B) & (A V B) = (B V Ā) & (B V A) = B V (Ā & A) = B V 0.

(Ā V B) & (A V B) = (B V Ā) & (B V A) = B V (Ā & A) = B V 0 = B.
А сейчас пришла пора подвести итоги урока.
На этом уроке мы с вами вспомнили основные логические операции и логические элементы. В соответствии с правилами построили таблицу истинности для логического выражения, а также логическую схему. Вспомнили основные свойства логических операций и упростили логическое выражение, исходя из этих правил.

 Получите свидетельство
Получите свидетельство Вход
Вход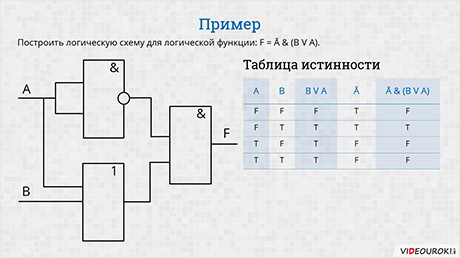



 0
0 7585
7585

