–Тема нашего урока «Задачи на совместное выполнение работы».

– Коллега, мне кажется, мы забыли представиться.
– М-да. Действительно. Мы профессора математики Примеркина и Задачкин.
– Именно нас сегодня пригласили к вам на урок, объяснить решение задач на совместное выполнение работы.
– Ну что, коллега, приступим к объяснению задач.
– Я бы не торопилась. Сначала необходимо выяснить очень важный момент. В таких задачах всегда используется один и тот же набор величин. Величины железно связаны между собой и образуют формулу-ключ. Именно этим ключиком и открывается решение любых задач на работу. Разберёмся, из каких же величин состоит формула-ключ. Их, величин, всего ничего. Три.
Первая величина в задачах на работу – это время. Слово простое и привычное. В данных задачах – это время, за которое выполняется та или иная работа. Измеряется, как вы догадываетесь, в секундах, минутах, часах, сутках и так далее. Обозначать время мы будем латинской буквой t.
Вторая величина – объём работы. Тоже вполне всё понятно. Сколько всего сделано деталей, налито воды, вспахано полей и так далее. Измеряется, соответственно, в тех единицах, о которых идёт речь в задаче. В деталях, литрах, полях и т.д. Будем обозначать объём работы большой латинской буквой А.
Третья величина менее привычна. Это – производительность. Слово может и смутить кого-то, да... Но, по сути, это просто скорость работы. И всё! Кто-то (или что-то) работает быстрее, а кто-то (что-то) – медленнее. Обычное дело. Обозначим производительность маленькой латинской буквой v.
Из этих величин можно составить формулу для решения задач:
v · t = А, где v – это скорость работы (или производительность), t – время работы, А – вся выполненная работа, т.е. объём работы. Это и есть формула-ключ для решения любых задач на работу.
Из этой формулы мы можем вывести и формулу нахождения времени и формулу нахождения выработки, т.е. производительности труда или скорости работы.

Можно называть и так, и эдак. Если производительность умножить на время получится объём выполненной работы, то чтобы найти время, надо объём работы разделить на производительность. А чтобы найти производительность, надо объём работы разделить на время.
– Что-то очень знакомая формула... А-а-а, так она напоминает формулу на движение. Скорость умножить на время, получается расстояние.

Только в тех задачах скорость движения, а в этих скорость работы. В тех задачах весь пройденный путь, а в этих – вся выполненная работа.
– А теперь, коллега, можно перейти к задачам. Вот первая из них.
Марина может за час набрать 10 страниц текста, а Наташа 8 страниц. За какое время они смогут набрать 90 страниц текста, работая вместе?
Давайте составим таблицу.

В ней будет три колонки. Первую назовём выработка за 1 ч., т.е. производительность труда. Вторая – время работы, третья – вся выполненная работа.
– Точно как в задачах на движение. Сначала выработка за 1 час, т.е. скорость работы, потом время работы. А потом весь путь, ой, т.е. вся выполненная работа.
– Совершенно верно, коллега. Ну, продолжим заполнять таблицу. Итак, мы знаем, что производительность труда Марины – это 10 страниц текста за каждый час и производительность труда Наташи – 8 страниц за каждый час. Ещё нам известна выполненная ими совместно работа – это 90 страниц. Они работали вместе, поэтому и время работы у них одинаковое и именно его мы и должны узнать. Нам известно количество станиц, напечатанных совместно. А скорость их работы, т.е. выработку – каждой из них по отдельности – это 10 страниц и 8 страниц.
А теперь составим план решения задачи.

Чтобы найти время совместной работы Марины и Наташи, надо знать две величины: всю работу (т.е. общее количество страниц) и совместную выработку за 1 час. Первая величина известная: надо набрать всего 90 страниц текста. А вторую мы найдём, сложив выработку Марины с выработкой Наташи.
1) 10 + 8 = 18 (стр.) – наберут за час Марина и Наташа вместе (т.е. совместная выработка за 1 час).
Теперь мы знаем объём совместной работы: 90 страниц и совместную выработку – 18 страниц в час, значит, мы можем найти время их работы.

Это мы найдём действием деления.
2) 90 : 18 = 5 (ч) – будут работать вместе Марина и Наташа.
Ответ: вместе Марина и Наташа наберут 90 страниц текста за 5 часов.
Но если вы хорошо подумаете, то найдёте ещё несколько способов решения этой задачи. По секрету, у меня их целых пять.
– Коллега, вернёмся к нашей задаче. При её решении мы воспользовались формулой t = А : v.
Чтобы найти время выполнения работы, надо работу разделить на производительность.
Теперь давайте решим мою задачу.
Для открытия картинной галереи необходимо изготовить 180 рамок для картин. Одна бригада мастеров может сделать эту работу за 45 дней, а другая за 36. За сколько дней эти бригады смогут вместе сделать рамки?
Ну, давайте заполним таблицу и для этой задачи.

В этой таблице тоже будет три столбика. Производительность труда, количество дней и вся выполненная работа. Обратите внимание, что эта таблица такая же, только вместо слова время используется количество дней. А ведь это тоже время выполнения работы. Но в этой таблице мы добавили только одну дополнительную строчку, в которой будет показано то, что делается совместно. Заполняем таблицу. Выработка ни первой, ни второй бригады, тем более их совместная, нам неизвестна. Зато мы знаем, что первая бригада за 45 дней изготовит 180 рамок. А вторая бригада те же 180 рамок изготовит за 36 дней. Нам надо узнать, за сколько дней они это сделают, работая вместе. Составляем план решения задачи.

Для того чтобы узнать, за сколько дней две бригады сделают все рамки надо знать, сколько всего рамок и совместную выработку. Сколько всего рамок, мы знаем – 180. А совместная выработка нам неизвестна. Чтобы узнать совместную выработку, т.е. производительность труда, нам нужно знать, выработку первой бригады и выработку второй бригады. Ни то, ни другое нам пока неизвестно. Но нам известно объём работы и количество дней на выполнение этой работы каждой из бригад. У первой бригады – 180 рамок за 45 дней. У второй бригады – 180 рамок за 36 дней. Воспользуемся формулой нахождения производительности труда.
v = А : t
Значит, выработку каждой бригады мы можем найти действием деления.
1) 180 : 45 = 4 (рамки) – делает за 1 день первая бригада мастеров
2) 180 : 36 = 5 (рамок) – делает за 1 день вторая бригада мастеров
Теперь мы знаем выработку первой и второй бригад по отдельности и можем узнать их совместную выработку действием сложения.
3) 4 + 5 = 9 (рамок) – совместная выработка
Ну, а теперь, когда мы узнали совместную выработку, мы можем узнать, сколько дней понадобится двум бригадам на изготовление 180 рамок, если они будут работать совместно. Т.к. нам надо найти количество дней, т.е. время работы, воспользуемся формулой t = А : v. Значит, количество дней находим действием деления.

4) 180 : 9 = 20 (дней) – понадобится двум бригадам на выполнение работы.
Ответ: на изготовление 180 рамок двум бригадам понадобится 20 дней.
Обратите внимание на то, что, работая вместе, две бригады тратят меньше времени, чем каждая из них, работая по отдельности. Вот что значит работать дружно.
– Ну вот мы, коллега, и рассмотрели задачи на совместное выполнение работы. Надеемся, что теперь, вы, ребята, без труда справитесь с решением таких задач.
– А я желаю вам в этом успехов.

 Получите свидетельство
Получите свидетельство Вход
Вход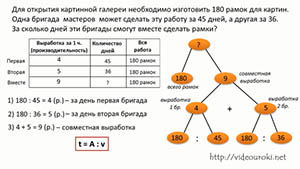



 0
0 6395
6395

