Различные варианты программирования циклического алгоритма

Вопросы:

·     Способы организации циклов при решении задач.

Задача: Определить, является ли целое число n простым. Число n пользователь вводит с клавиатуры. 4 ≤ n ≤ 2 000 000 000.

Простым называется целое число, которое не делится нацело ни на одно целое число, кроме единицы и себя самого. Для того, чтобы определить, является ли число n простым, нам достаточно проверить, не делится ли оно на какое-нибудь из целых чисел на промежутке от 2 до .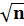

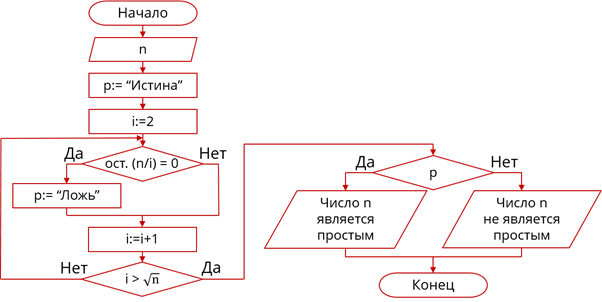
Сперва рассмотрим вариант решения этой задачи при помощи цикла с параметром. Составим блок-схему алгоритма решения задачи. Сперва считаем значение n введённое пользователем. Для того, чтобы определить, является ли n простым, нам понадобится логическая переменная p. Присвоим ей значение «Истина», предположив, что n – простое число. Дальше будет следовать цикл для i от 2 до 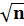, а в нём – условный оператор, который будет проверять, равен ли остаток от деления n на i 0. Если это условие будет выполняться, значит число n не является простым – и мы присвоим переменной p, значение «Ложь», в противном случае ничего делать не нужно. После цикла будет следовать условный оператор, который будет проверять значение переменной p. Если значение p – «Истина», значит n – простое число, выведем на экран поясняющее сообщение об этом. Если же значение p – «ложь», выведем на экран поясняющее сообщение о том, что число n не является простым.

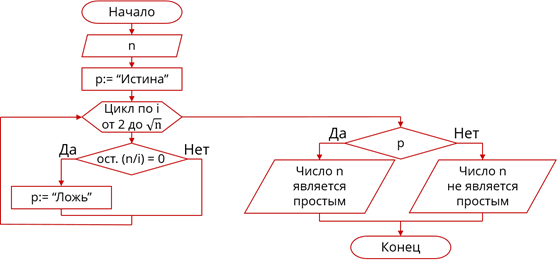
Блок-схема алгоритма

Теперь напишем программу по составленной блок-схеме. Назовём её prostoe_chislo. Для решения задачи нам понадобятся две целочисленные переменные: n и i. Так как n находится на промежутке от 4 до 2 000 000 000, а i изменяется в пределах от 2 до 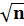, объявим их принадлежащими целочисленному типу integer. Так же нам понадобится логическая переменная p типа boolean.

Запишем логические скобки. Программа будет начинаться с оператора writeln, который будет выводить на экран поясняющее сообщение о том, что это программа, определяющая, является ли число n простым. Дальше будет следовать ещё один оператор write, который будет выводить на экран запрос на ввод числа n. После него будет оператор readln, считывающий значение переменной n. Затем будет оператор присваивания переменной p значения true. Теперь запишем цикл для i от 2 до .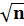

Квадратный корень из n извлекается с помощью функции sqrt. Так как эта функция возвращает значение вещественного типа, поэтому при вычислении результата могут быть погрешности, поэтому прибавим к корню из n единицу. Так же в цикле должно быть указано значение целого типа, приведём значение вещественного типа к целому с помощью функции округления round. Тело цикла будет содержать всего один условный оператор, поэтому логические скобки не требуются. Запишем условный оператор, его условием будет то, что остаток от деления n на i равен нулю. После служебного слова then будет следовать оператор присваивания переменной p значения false.

После цикла запишем условный оператор. В качестве его условия зададим значение логической переменной p. Она будет содержать значение истинности утверждения о том, что n – простое число. После слова then в этом условном операторе будет следовать оператор write, который выводит поясняющее сообщение о том, что n – простое число. После слова else будет следовать оператор write, выводящий на экран сообщение о том, что n не является простым числом.

program prostoe_chislo;

var

 n, i: integer;

 p: boolean;

begin

 writeln ('Программа, определяющая, является ли целое число n простым.');

 write ('n=');

 readln (n);

 p:=true;

 for i:=2 to round (sqrt(n)+1) do

  if n mod i=0

  then p:=false;

 if p

 then write ('Число ', n, ' является простым.')

 else write ('Число', n, ' не является простым.');

end.

Исходный код программы

Запустим программу на выполнение и зададим n = 33.

Число 33 действительно не является простым, так как делится нацело на 3. Снова запустим программу на выполнение и введём число n = 79.

Это число действительно является простым так как делится нацело лишь на себя и на 1.

Решение этой же задачи можно оформить также с помощью циклов с предусловием и с постусловием. Решим эту задачу при помощи цикла с постусловием. Изменим блок-схему составленного нами алгоритма. Уберём записанный нами цикл с параметром. Вместо него сначала присвоим переменной i значение 2. И запишем уже знакомый нам условный оператор, который проверяет, равен ли остаток от деления n на i нулю. В случае если это условие выполняется переменной p присвоим значение «Ложь». Дальше будет следовать оператор, увеличивающий значение переменной i на 1. Два последних оператора будут выполнятся до тех пор, пока i не станет больше 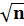. После цикла будет следовать условный оператор, со значением переменной p в качестве условия. Он будет выводить на экран поясняющее сообщение о том, является ли число n простым.

Изменённая блок-схема алгоритма

Изменим исходный код написанной нами программы в соответствии с блок-схемой. Для этого удалим из кода цикл определяющий, является ли n простым числом. Запишем вместо него оператор присваивания i значения 2, а также служебные слова repeat и until, с условием окончания работы цикла: i > sqrt (n) + 1. В начале тела цикла будет следовать условный оператор с условием: n mod i = 0. Если остаток от деления n на i действительно равен 0, присвоим p значение false. В конце тела цикла будет следовать оператор присваивания переменной i её значения, увеличенного на единицу. Код программы, следующий далее останется прежним…

i:=2;

repeat

 if n mod i=0

 then p:=false;

 i:=i+1;

until i>sqrt (n)+1;

Изменённый цикл определения делимости n

Запустим программу на выполнение и зададим n = 83.

Это число действительно является простым. Снова запустим программу и зададим n = 2 000 000 000.

Это число не является простым.

Сравним изменяющуюся часть исходного кода обеих программ. Очевидно, что первый вариант программы короче, и возможно у вас возникнет вопрос: «Для чего нужен второй вариант решения задачи?».

Ещё раз рассмотрим наш метод решения. Для того, чтобы определить является ли число n простым, мы последовательно проверяем не делится ли оно на все числа в промежутке от 2 до 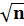. Однако единожды проверив, не делится ли n на 2 мы можем больше не проверять его делимость на чётные числа. Перебор возможных делителей можно сократить таким образом потому, что в разложении всех чётных чисел на простые множители будет присутствовать число 2. Более того можно остановить перебор возможных делителей числа n найдя среди них хотя бы один действительный.

Изменим блок-схему алгоритма решения задачи. Изменим часть алгоритма, определяющую, является ли число n простым. После считывания числа n определим, не делится ли оно на 2 и результат этого высказывания присвоим переменной p. Дальше присвоим i значение 3 и запишем условный оператор с условием что остаток от деления n на i равен 0. В случае если условие выполняется, после него будет следовать оператор присваивания p значения «Ложь». Теперь увеличим значение переменной i на 2, чтобы пропустив следующее, по порядку число, которое является чётным, перейти сразу к следующему за ним нечётному числу. Дальше будет ветвление с условием i больше 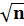. Если это условие не выполняется –вернёмся к выполнению предыдущего условного оператора, если же условие выполняется – закончим выполнение цикла. После цикла будет следовать уже знакомый нам условный оператор, который в зависимости от значения p выводит на экран поясняющее сообщение о том, является ли число n простым.

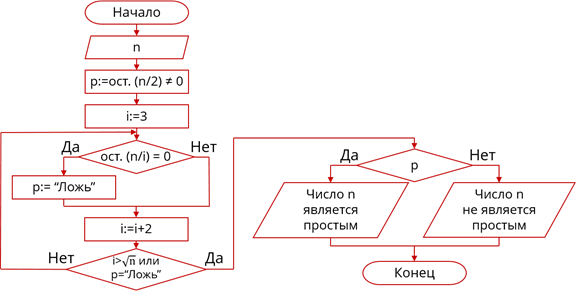
Изменённая блок-схема алгоритма

Изменим исходный код программы. Для этого после считывания значения n, присвоим p значение истинности высказывания о том, что остаток от деления n на 2 неравен 0. Дальше переменной i вместо двух присвоим значение 3. В теле цикла изменим оператор увеличения значения i на 1, так чтобы значение i увеличивалось на 2. А к условию окончания работы цикла допишем or (p=false).

p:=n mod 2<>0;

i:=3;

repeat

 if n mod i=0

 then p:=false;

 i:=i+2;

until (i>sqrt (n)+1) or (p=false);

Изменённый цикл определения делимости n

Запустим программу на выполнение и зададим n = 47.

Это число действительно является простым. Снова запустим программу и зададим n = 49.

Это число не является простым, потому что нацело делится на 7.

Нам удалось сократить перебор возможных делителей числа n почти наполовину, однако у написанной нами программы есть один недостаток. Он кроется в том, что тело цикла с постусловием выполняется хотя бы один раз. То есть даже в случае, если число n делится на 2, тело цикла с постусловием выполнится, прежде чем будет проверено его условие. Чтобы этого не происходило уберём цикл с постусловием и запишем на его месте цикл с предусловием. Условием продолжения его работы будет i <= 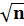 и p = «Истина». Тело цикла будет тем же что и у цикла с постусловием. После цикла будет следовать всё тот же условный оператор, который в зависимости от значения p будет выводить на экран сообщение о том, является ли число n простым.

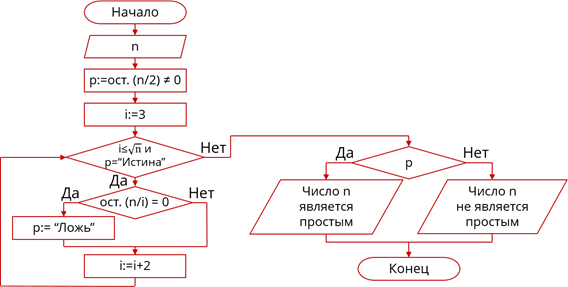
Изменённая блок-схема алгоритма

Изменим исходный код нашей программы, для этого удалим служебные слова, соответствующие циклу с постусловием, repeat и until вместе с условием окончания работы цикла. Вместо служебного слова repeat запишем оператор цикла с предусловием while и условием начала работы: (i <= +1) and (p = true). Тело цикла, так как оно содержит больше одного оператора, заключим в логические скобки.

while (i<sqrt(n)+1) and (p=true) do

begin

 if n mod i=0

 then p:=false;

 i:=i+2;

end;

Изменённый цикл определения делимости n

Снова запустим программу на выполнение и зададим n = 73.

Это число действительно является простым. Снова запустим программу и зададим n = 1023.

Это число не является простым так как нацело делится на 3. Программа работает правильно задача решена.

Важно запомнить:

·     Цикл с параметром можно реализовать через цикл с постусловием.

·     Циклы с предусловием и постусловием часто взаимозаменяемы.